Презентация на тему Решение систем неравенств

Тема «Решение систем неравенств»
Цель
В ходе изучения темы учащиеся должны знать,что множество решений системы неравенств есть пересечение множеств решений неравенств, входящих в эту систему
2) Научить решать системы, составленные из двух линейных неравенств.

Повторение
Математический диктант
Изучение нового материала
Закрепление
Итог урока
План урока

Повторение
а≤х ≤ в,
называется отрезком
и обозначается
[а ; в]
Если а < в, то множество чисел х,
удовлетворяющих неравенствам
а<х < в,
называется интервалом
и обозначается
(а ; в)
а<х ≤ в и а≤х < в
называются полуинтервалами
и обозначаются
(а ; в] и [а ; в)

Числовые промежутки
Отрезки
[ a; в]
Интервалы
(а ; в)
Полуинтервалы
[ a; в) или ( а; в]
Повторение
Лучи
х>а или х< в

Математический диктант
Запишите числовой промежуток, служащий множеством решений неравенства

Проверь себя
[3;6],
[1,5;5]

Математический диктант
Какие из целых чисел принадлежат промежутку (-1; 3,6], [-6,6;1)?

Проверь себя
0,1,2,3
-6,-5,-4,-3,-2,0

Математический диктант
Укажите наибольшее и наименьшее целое число, принадлежащее промежуткам
(-8; 8), (-6;-2)

Проверь себя
Наибольшее 7
Наименьшее -7
Наибольшее -3
Наименьшее -5

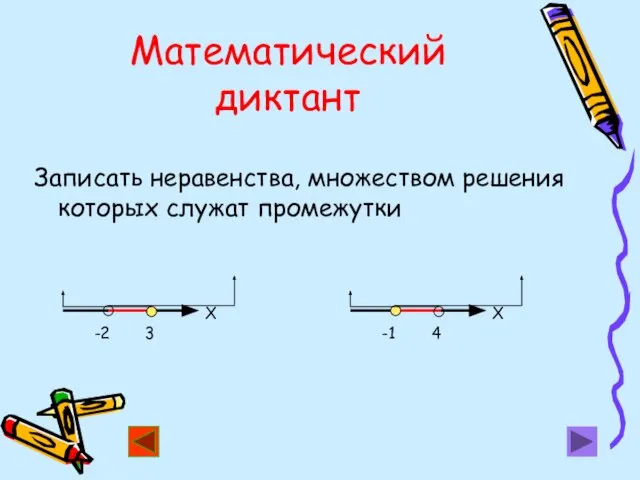
Математический диктант
Записать неравенства, множеством решения которых служат промежутки
-2
3
Х
-1
4
Х

Проверь себя

Изучение нового материала
Чтобы решить систему линейных неравенств, достаточно решить каждое из входящих в неё неравенство и найти пересечение множеств их решений.

Рассмотрим примеры решения задач
5Х-1 > 3( Х+ 1),
2(Х+4) > Х+5
Решим первое неравенство
5Х-1.> 3Х+3, 2Х > 4, Х > 2
Решим второе неравенство
2Х+8 > Х+ 5, Х > -3

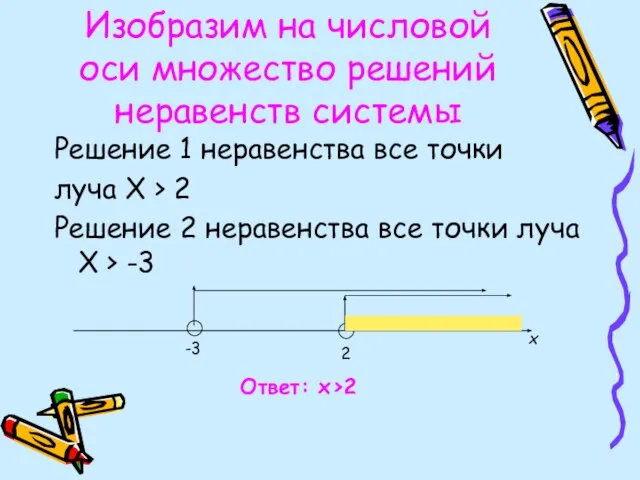
Изобразим на числовой оси множество решений неравенств системы
Решение 1 неравенства все точки
луча Х > 2
Решение 2 неравенства все точки луча Х > -3
-3
2
Ответ: x>2
x

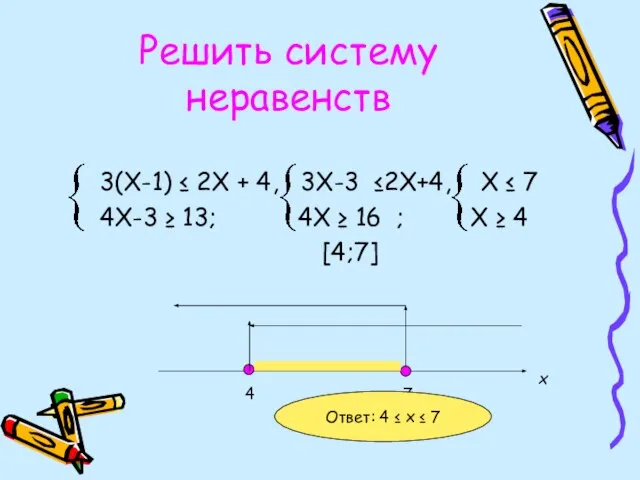
Решить систему неравенств
3(Х-1) ≤ 2Х + 4, 3Х-3 ≤2Х+4, Х ≤ 7
4Х-3 ≥ 13; 4Х ≥ 16 ; Х ≥ 4
[4;7]
4 7
x
Ответ: 4 ≤ x ≤ 7