Содержание
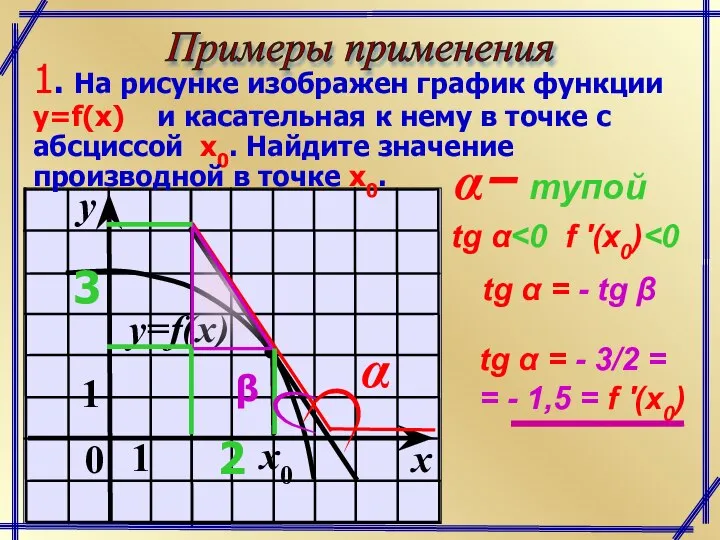
- 2. Примеры применения 1. На рисунке изображен график функции y=f(x) и касательная к нему в точке с
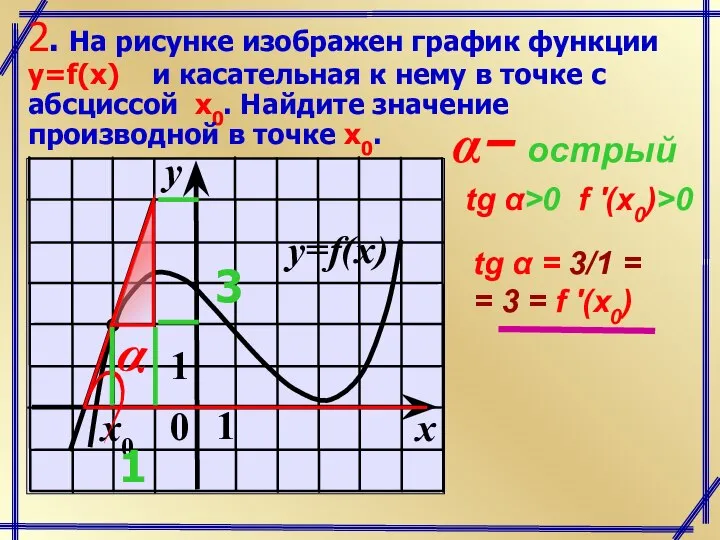
- 3. 2. На рисунке изображен график функции y=f(x) и касательная к нему в точке с абсциссой x0.
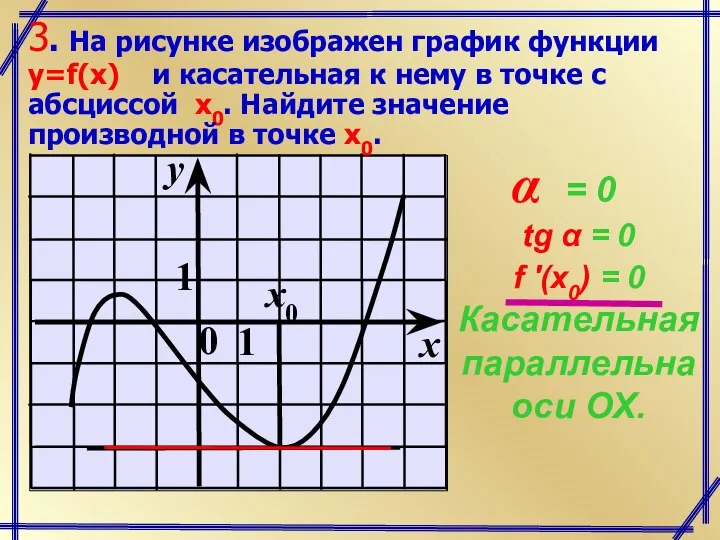
- 4. 3. На рисунке изображен график функции y=f(x) и касательная к нему в точке с абсциссой x0.
- 5. Решение. f '(x₀) = tg α = к Угловой коэффициент касательной равен -2 .
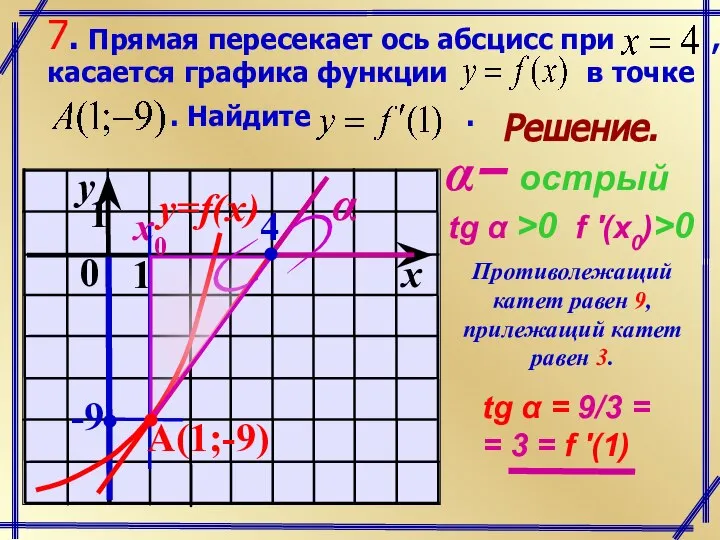
- 6. Решение. x0 − острый tg α >0 f '(x0)>0 Противолежащий катет равен 9, прилежащий катет равен
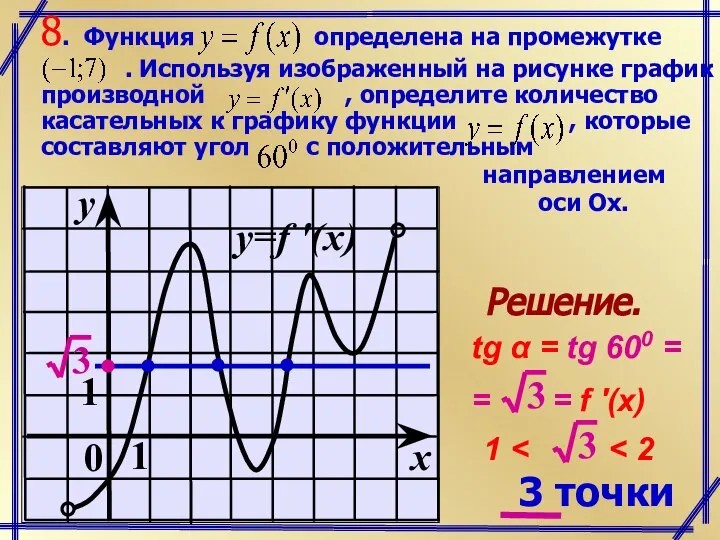
- 7. Решение. 3 точки
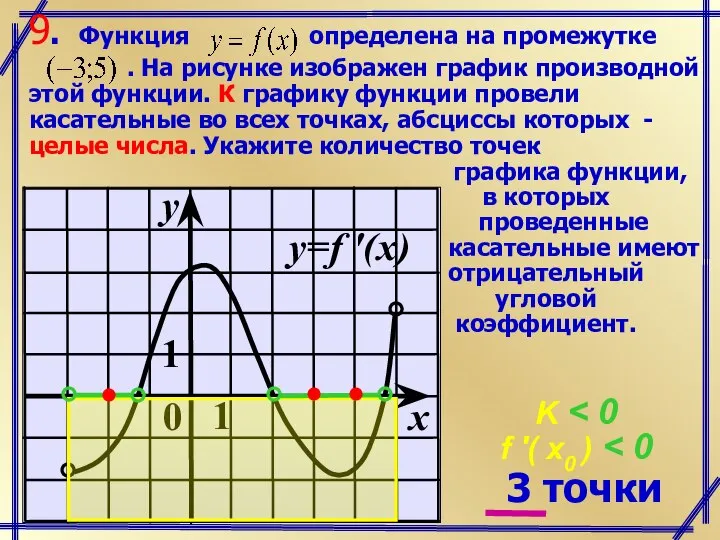
- 8. K f '( x0 ) 3 точки
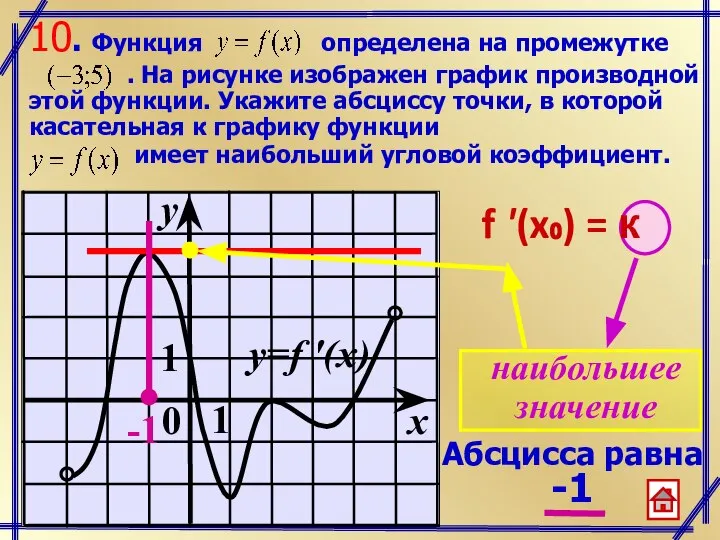
- 9. f '(x₀) = к Абсцисса равна -1
- 11. Скачать презентацию

 Стохастические процессы
Стохастические процессы Презентация на тему Графическое решение уравнений
Презентация на тему Графическое решение уравнений  Старинные меры массы и длины
Старинные меры массы и длины Комплексные числа. Все формы
Комплексные числа. Все формы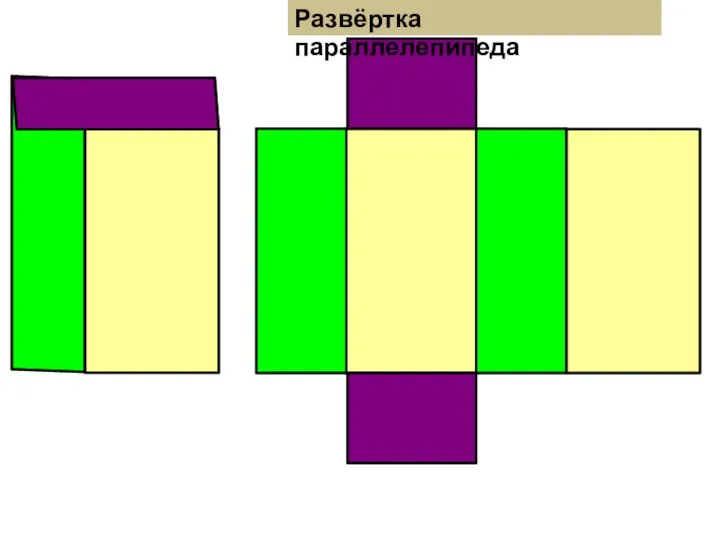 Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс
Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс Тригонометрические уравнения
Тригонометрические уравнения Квадратичная функция и её график. Методические материалы урока
Квадратичная функция и её график. Методические материалы урока Презентация на тему Объём многогранника
Презентация на тему Объём многогранника  Сближение меридианов. Международное геомагнитное аналитическое поле IGRF
Сближение меридианов. Международное геомагнитное аналитическое поле IGRF Задачи про форматы листов. Решение практико-ориентированных задач
Задачи про форматы листов. Решение практико-ориентированных задач Метод обратной матрицы решения систем линейных уравнений
Метод обратной матрицы решения систем линейных уравнений Методика работы с задачей на круговое движение
Методика работы с задачей на круговое движение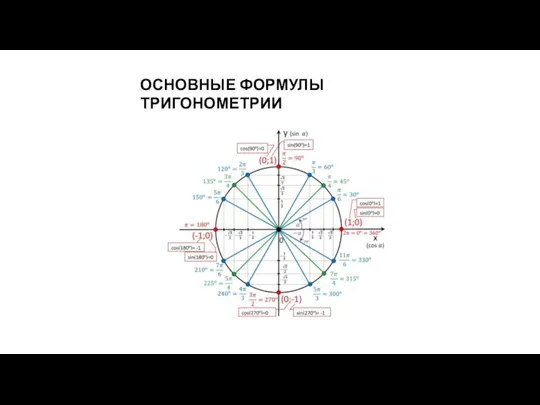 Основные формулы тригонометрии
Основные формулы тригонометрии Деление обыкновенных дробей
Деление обыкновенных дробей 7490_md_sin_cos_tg_0
7490_md_sin_cos_tg_0 Пирамида и её элементы. Правильная пирамида
Пирамида и её элементы. Правильная пирамида Математика вокруг нас
Математика вокруг нас Время. Единицы времени
Время. Единицы времени Первый замечательный предел
Первый замечательный предел Математика ЕГЭ. Углы и прямые
Математика ЕГЭ. Углы и прямые Линейная функция и её график
Линейная функция и её график Теория вероятностей в задачах ЕГЭ
Теория вероятностей в задачах ЕГЭ Основы логистики
Основы логистики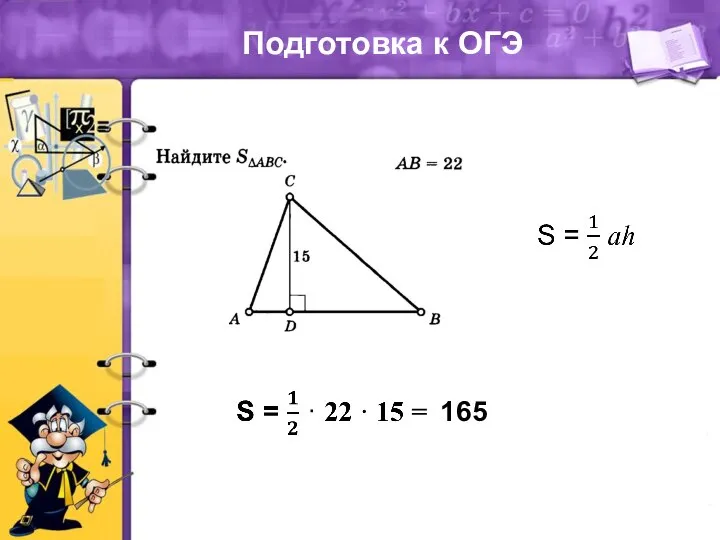 Теорема площади треугольника. Подготовка к ОГЭ
Теорема площади треугольника. Подготовка к ОГЭ Прямоугольник. Геометрия 8 класс
Прямоугольник. Геометрия 8 класс Логарифмические выражения
Логарифмические выражения Презентация по математике "Применение приёмов интерактивного обучения на уроках математики" -
Презентация по математике "Применение приёмов интерактивного обучения на уроках математики" -  Презентация на тему Метод координат в пространстве
Презентация на тему Метод координат в пространстве