- Главная
- Математика
- Теорема о прямой, перпендикулярной к плоскости

Содержание
- 3. Доказательство Пусть нам дана прямая a и точка М. Докажем, что существует плоскость γ, которая проходит
- 4. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
- 5. Доказательство. Пусть дана плоскость α и точка М (см. рис. 2). Нужно доказать, что через точку
- 6. В плоскости γ через точку М проведем прямую с, перпендикулярную прямой b. Прямая с перпендикулярна b
- 11. Скачать презентацию
Слайд 3Доказательство
Пусть нам дана прямая a и точка М. Докажем, что существует плоскость γ, которая проходит
Доказательство Пусть нам дана прямая a и точка М. Докажем, что существует плоскость γ, которая проходит
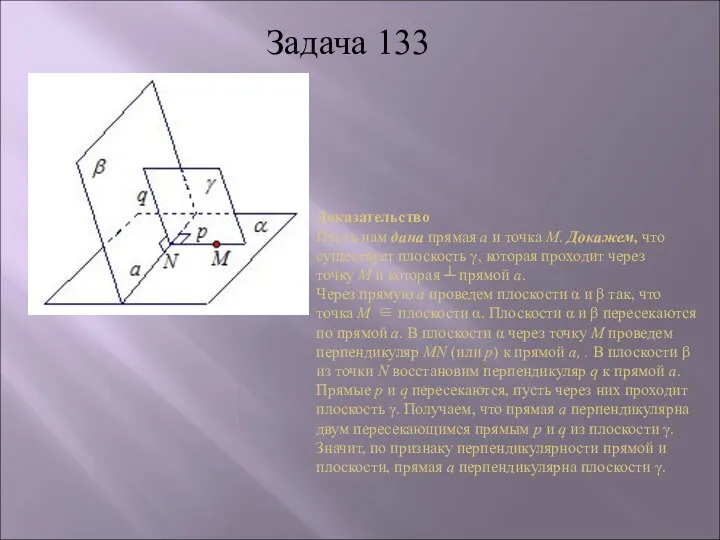
через точку М и которая ┴ прямой а.
Через прямую а проведем плоскости α и β так, что точка М ∈ плоскости α. Плоскости α и β пересекаются по прямой а. В плоскости α через точку М проведем перпендикуляр MN (или р) к прямой а, . В плоскости β из точки N восстановим перпендикуляр q к прямой а. Прямые р и q пересекаются, пусть через них проходит плоскость γ. Получаем, что прямая а перпендикулярна двум пересекающимся прямым р и q из плоскости γ. Значит, по признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости γ.
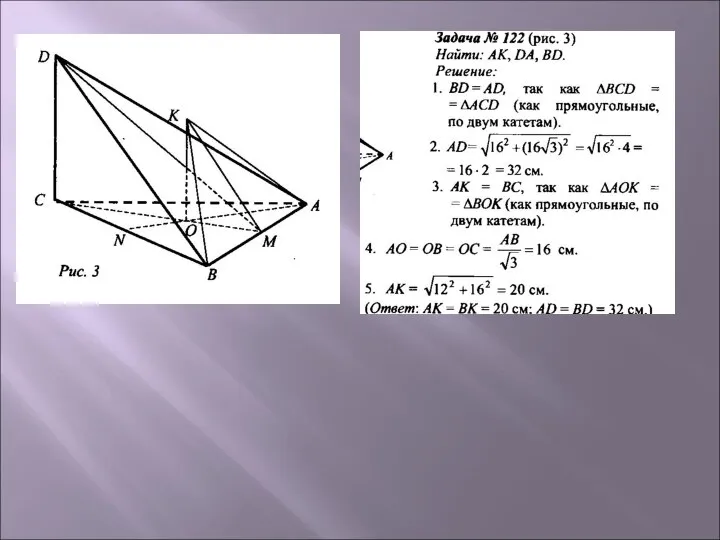
Задача 133
Слайд 4Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом
Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом
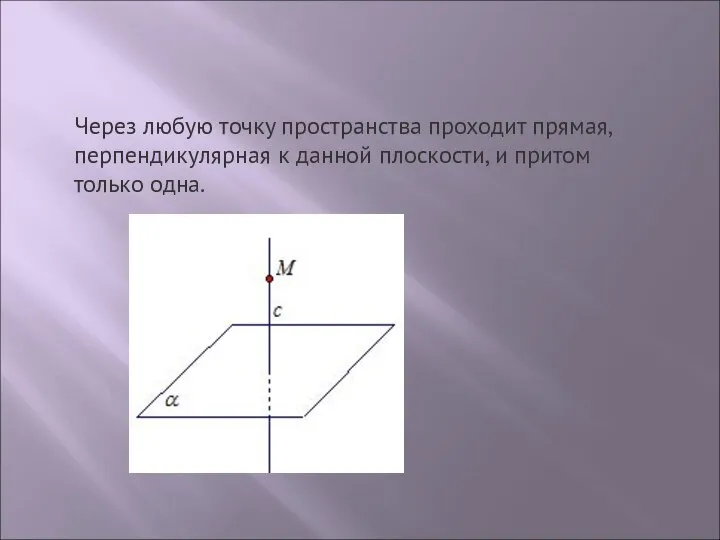
только одна.
Слайд 5Доказательство.
Пусть дана плоскость α и точка М (см. рис. 2). Нужно доказать, что через
Доказательство.
Пусть дана плоскость α и точка М (см. рис. 2). Нужно доказать, что через
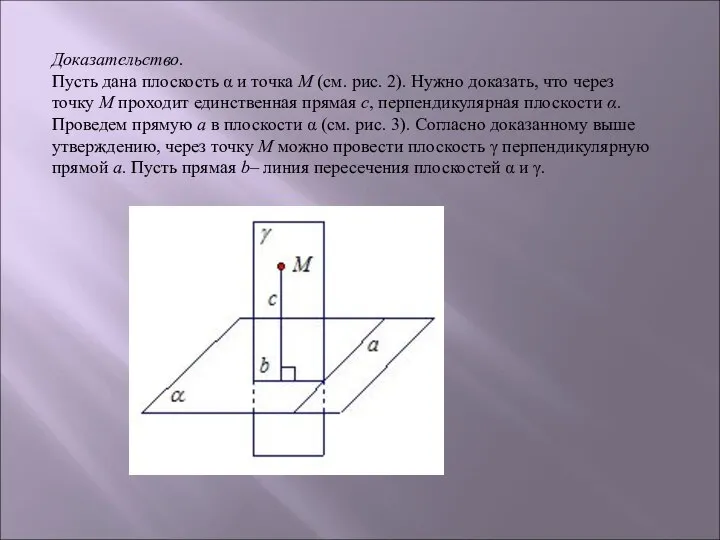
точку М проходит единственная прямая с, перпендикулярная плоскости α.
Проведем прямую а в плоскости α (см. рис. 3). Согласно доказанному выше утверждению, через точку М можно провести плоскость γ перпендикулярную прямой а. Пусть прямая b– линия пересечения плоскостей α и γ.
Проведем прямую а в плоскости α (см. рис. 3). Согласно доказанному выше утверждению, через точку М можно провести плоскость γ перпендикулярную прямой а. Пусть прямая b– линия пересечения плоскостей α и γ.
Слайд 6В плоскости γ через точку М проведем прямую с, перпендикулярную прямой b.
Прямая с перпендикулярна b по построению, прямая с перпендикулярна а (так как прямая а перпендикулярна
В плоскости γ через точку М проведем прямую с, перпендикулярную прямой b.
Прямая с перпендикулярна b по построению, прямая с перпендикулярна а (так как прямая а перпендикулярна

плоскости γ, а значит, и прямой с, лежащей в плоскости γ). Получаем, что прямая с перпендикулярна двум пересекающимся прямым из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая с перпендикулярна плоскости α. Докажем, что такая прямая с единственная.
Предположим, что существует прямая с1, проходящая через точку М и перпендикулярная плоскости α. Получаем, что прямые с и с1 перпендикулярны плоскости α. Значит, прямые с и с1 параллельны. Но по построению прямые с и с1 пересекаются в точке М. Получили противоречие. Значит, существует единственная прямая, проходящая через точку М и перпендикулярная плоскости α, что и требовалось доказать.
Предположим, что существует прямая с1, проходящая через точку М и перпендикулярная плоскости α. Получаем, что прямые с и с1 перпендикулярны плоскости α. Значит, прямые с и с1 параллельны. Но по построению прямые с и с1 пересекаются в точке М. Получили противоречие. Значит, существует единственная прямая, проходящая через точку М и перпендикулярная плоскости α, что и требовалось доказать.
- Предыдущая
Стили открыток ручной работыСледующая -
Поп-арт

 Случаи вычитания 11 -
Случаи вычитания 11 - Статистические графики
Статистические графики математика гр 32 парність-2.docx
математика гр 32 парність-2.docx Число та цифра 6
Число та цифра 6 Конус. Виды конусов. Конусы в нашей жизни
Конус. Виды конусов. Конусы в нашей жизни Сечения в многогранниках
Сечения в многогранниках Уравнение линии на плоскости. Уравнение фигуры. Уравнение окружности
Уравнение линии на плоскости. Уравнение фигуры. Уравнение окружности Решение задач с помощью уравнений
Решение задач с помощью уравнений Решение задач на движение
Решение задач на движение Понятие спирали
Понятие спирали Геометрические построения
Геометрические построения Элементы теории вероятностей
Элементы теории вероятностей Проценты
Проценты Математические ребусы
Математические ребусы Площади. ОГЭ
Площади. ОГЭ Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Текстовые задачи на движение по прямой
Текстовые задачи на движение по прямой Основное свойство дроби
Основное свойство дроби Две задачи на дроби
Две задачи на дроби Статистические гипотезы
Статистические гипотезы Собираем ягоды. Математика 1 класс. Итоговое повторение. Тренажёр
Собираем ягоды. Математика 1 класс. Итоговое повторение. Тренажёр Конструктивные объекты
Конструктивные объекты Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики?
Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики? Презентация по математике "Что такое понятие" -
Презентация по математике "Что такое понятие" -  Параллельность плоскостей
Параллельность плоскостей Экономический биатлон. “Экономика и математика”. Финал
Экономический биатлон. “Экономика и математика”. Финал Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними
Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними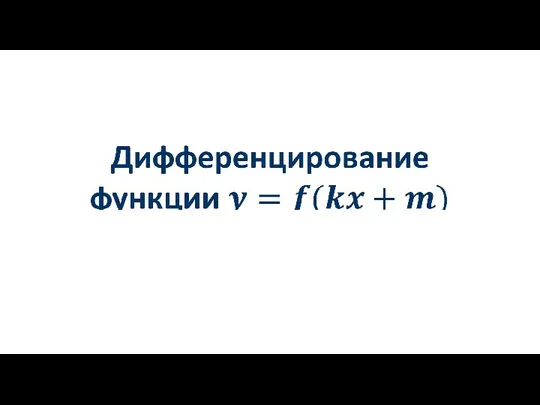 Дифференцирование функции y=f(kx+m)
Дифференцирование функции y=f(kx+m)