Определенный интеграл

Определение 1:
Сумма вида
называется интегральной суммой для f(x) на отрезке
Определение 2:
Устремим максимальную длину отрезков к нулю. При этом
. Тогда интегральная сумма стремится к некоторому пределу
называется определенным интегралом от функции f(x) на отрезке (или в отрезке от a до b). a и b называются нижним и верхним пределом интегрирования.

Геометрический смысл
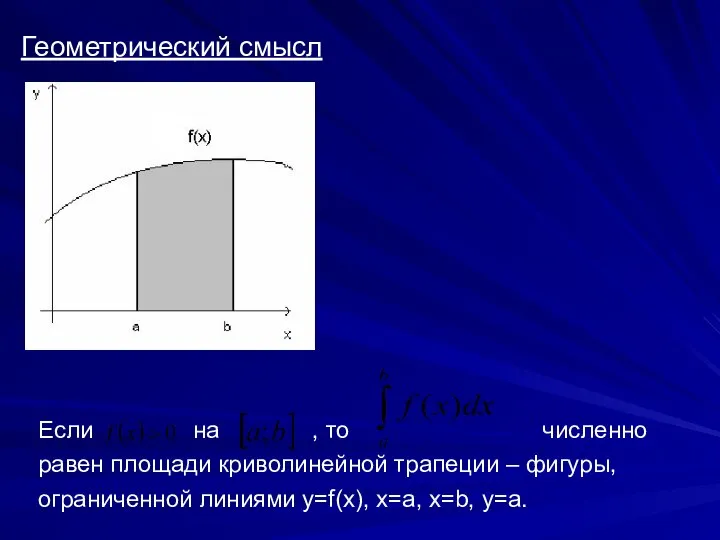
Если на , то численно равен площади криволинейной трапеции – фигуры, ограниченной линиями y=f(x), x=a, x=b, y=a.

Основные свойства определенного интеграла
Если , то
- формула
Ньютона-Лейбница
Здесь F(x) – первообразная для f(x).
2)

3)
Т.е. при перестановке пределов интегрирования меняется знак интеграла.
4)
Определенный интеграл с одинаковыми пределами интегрирования равен 0.

5)
Т.е. отрезок интегрирования можно разбивать на части.
6)

Примеры
1.Вычислить
Найдем первообразную
Возьмем
Тогда получаем по формуле Ньютона-Лейбница

2. Вычислить
Найдем первообразную
Выберем
Тогда