Электронные системы ДВС. Метод наименьших квадратов

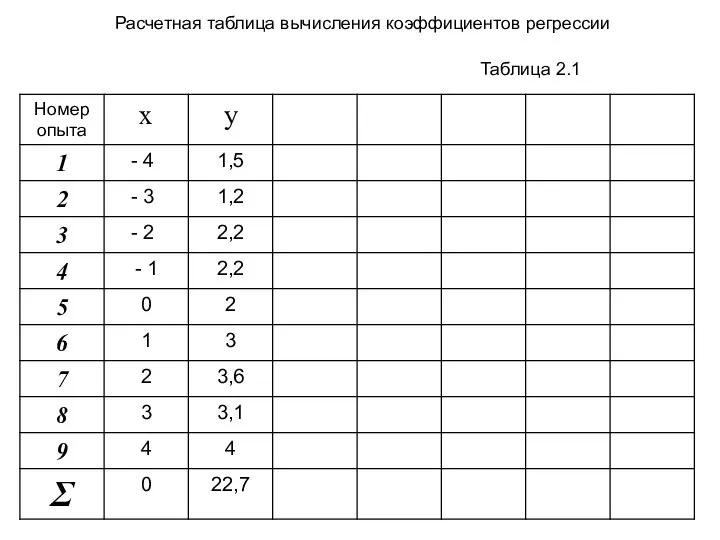
Пример 1.
В результате проведенного эксперимента была получена следующая таблица (см. след. слайд).
Значения экспериментально полученных значений нанесены на график (см. след. слайд).

Таблица 2.1
Расчетная таблица вычисления коэффициентов регрессии

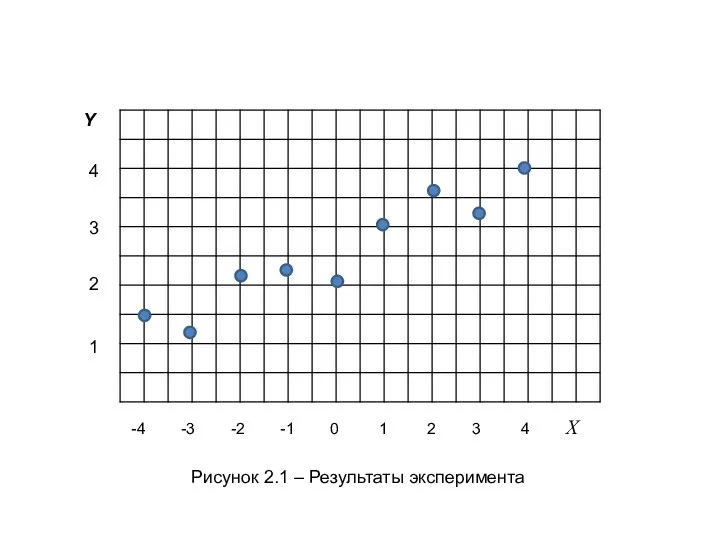
-4 -3 -2 -1 0 1 2 3 4 Х
1
2
3
4
Y
Рисунок 2.1 – Результаты эксперимента

На рис.2.1 точками показаны значения y в зависимости от х, полученные в результате эксперимента.
Так как явно прослеживается линейная зависимость, полагаем, что уравнение этой зависимости имеет вид:
Здесь неизвестны коэффициенты b0 и b1.
Для их определения воспользуемся методом наименьших квадратов.
(2.1)

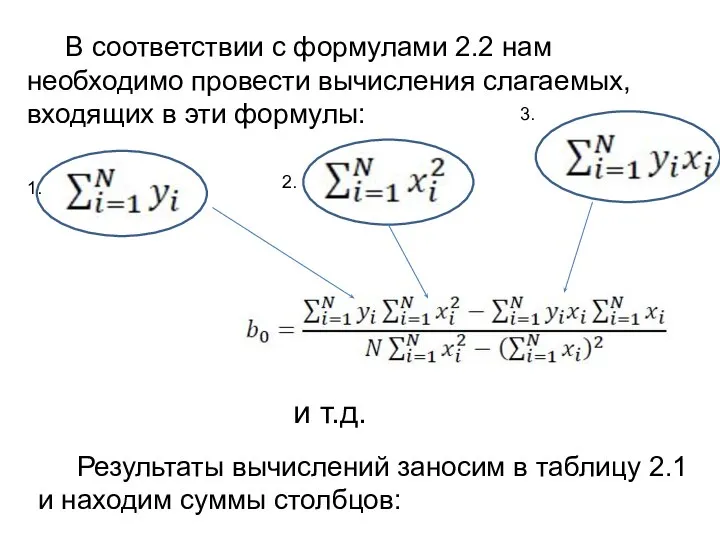
В соответствии с методикой метода наименьших квадратов коэффициенты b0 и b1 вычисляются по формулам:
(2.2)

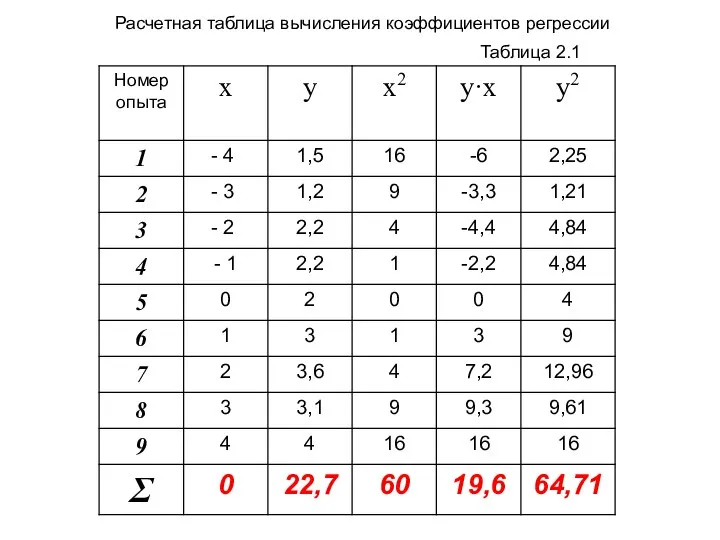
В соответствии с формулами 2.2 нам необходимо провести вычисления слагаемых, входящих в эти формулы:
1.
2.
3.
и т.д.
Результаты вычислений заносим в таблицу 2.1 и находим суммы столбцов:

Таблица 2.1
Расчетная таблица вычисления коэффициентов регрессии

Тогда:
=
22,7 · 60 – 19,6 ·0
_______________
9 ·60 - 0
= 2,52
=
b0 = 2,52

Тогда:
b1 = 0,33
=
=

Таким образом, уравнение (2.1) запишется в виде:
На рис.2.2 (см. след. слайд) построен график искомого уравнения, построенный по формуле 2.3.
МНК гарантирует, что сумма всех отклонений между экспериментальными данными (точками) и построенной зависимостью (прямой) минимальна.
(2.3)