Точки экстремума функции

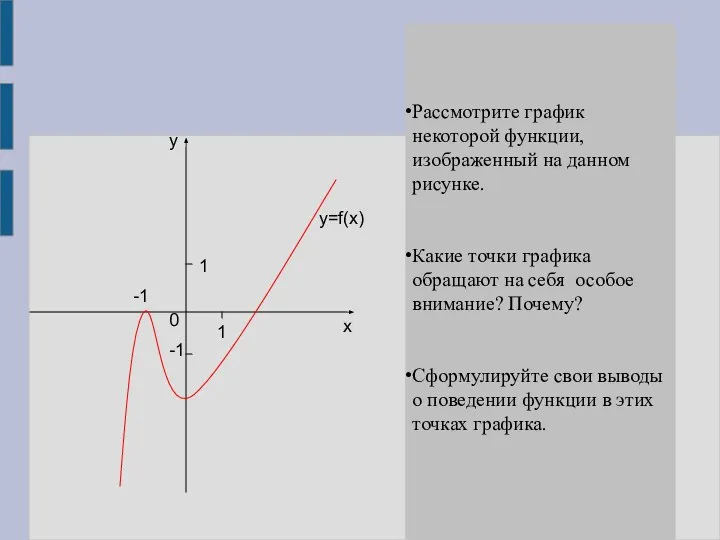
1
1
-1
0
х
у
-1
Рассмотрите график некоторой функции, изображенный на данном рисунке.
Какие точки графика обращают на себя особое внимание? Почему?
Сформулируйте свои выводы о поведении функции в этих точках графика.
y=f(x)

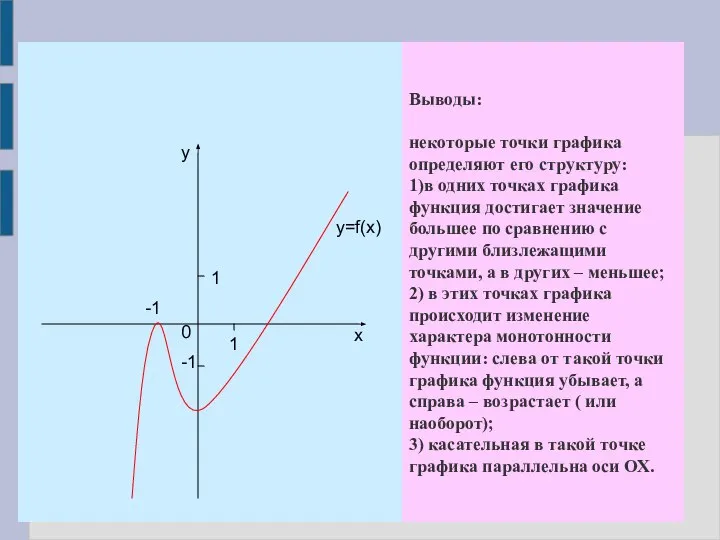
Выводы:
некоторые точки графика определяют его структуру:
1)в одних точках графика функция достигает значение большее по сравнению с другими близлежащими точками, а в других – меньшее;
2) в этих точках графика происходит изменение характера монотонности функции: слева от такой точки графика функция убывает, а справа – возрастает ( или наоборот);
3) касательная в такой точке графика параллельна оси ОХ.
1
1
-1
0
х
у
-1
y=f(x)

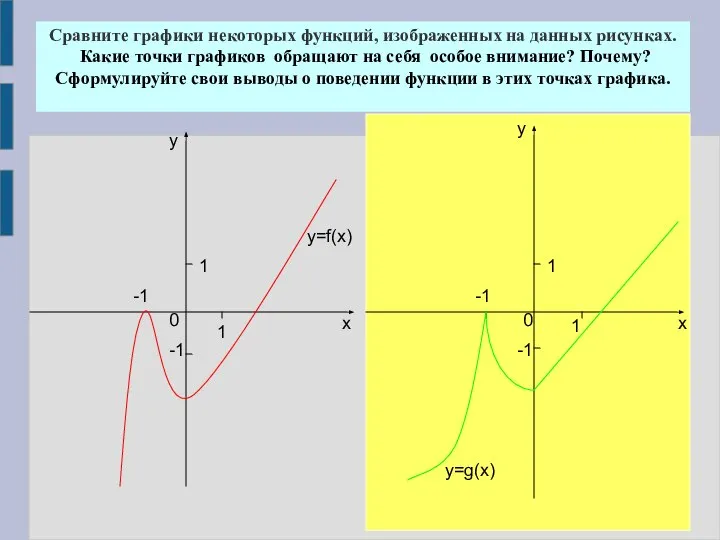
1
1
-1
0
х
у
-1
у
х
1
0
-1
1
-1
Сравните графики некоторых функций, изображенных на данных рисунках.
Какие точки графиков обращают на себя особое внимание? Почему?
Сформулируйте свои выводы о поведении функции в этих точках графика.
y=f(x)
y=g(x)

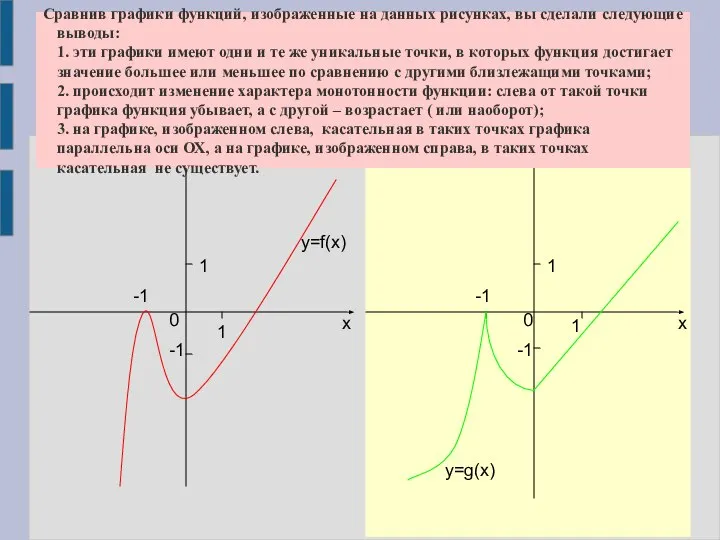
1
1
-1
0
х
у
-1
у
х
1
0
-1
1
-1
Сравнив графики функций, изображенные на данных рисунках, вы сделали следующие выводы:
1. эти графики имеют одни и те же уникальные точки, в которых функция достигает значение большее или меньшее по сравнению с другими близлежащими точками;
2. происходит изменение характера монотонности функции: слева от такой точки графика функция убывает, а с другой – возрастает ( или наоборот);
3. на графике, изображенном слева, касательная в таких точках графика параллельна оси ОХ, а на графике, изображенном справа, в таких точках касательная не существует.
y=f(x)
y=g(x)

Точки экстремума
Точка х0 называется точкой максимума функции f(x), если существует такая окрестность точки х0, что для всех х (кроме х0) из этой окрестности выполняется неравенство f(x) < f(х0).
Обозначается: Xmax, а значение функции в этой точке – Ymax ( не путать с Унаиб).
Точка х0 называется точкой минимума функции f(x), если существует такая окрестность точки х0, что для всех х (кроме х0) из этой окрестности выполняется неравенство f(x) > f(х0).
Обозначается: Xmin, а значение функции в этой точке – Ymin ( не путать с Унаим).
Точки минимума и точки максимума вместе называются точками экстремума.

В курсе математического анализа справедливо следующее утверждение:
Для того чтобы точка х0 была точкой экстремума функции f(x), необходимо, чтобы эта точка была критической точкой данной функции.

Верно ли обратное утверждение:
если х= х0 критическая точка
функции f(x), то в этой точке функция имеет экстремум?

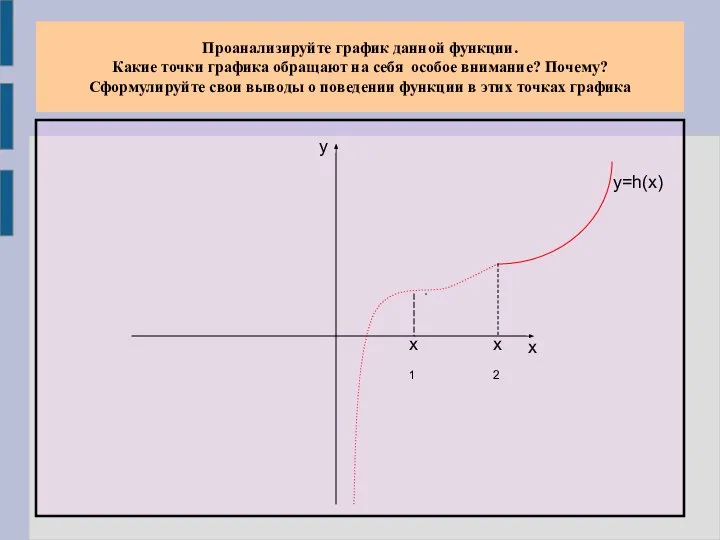
Проанализируйте график данной функции.
Какие точки графика обращают на себя особое внимание? Почему?
Сформулируйте свои выводы о поведении функции в этих точках графика
х1
х2
y=h(x)
x
y

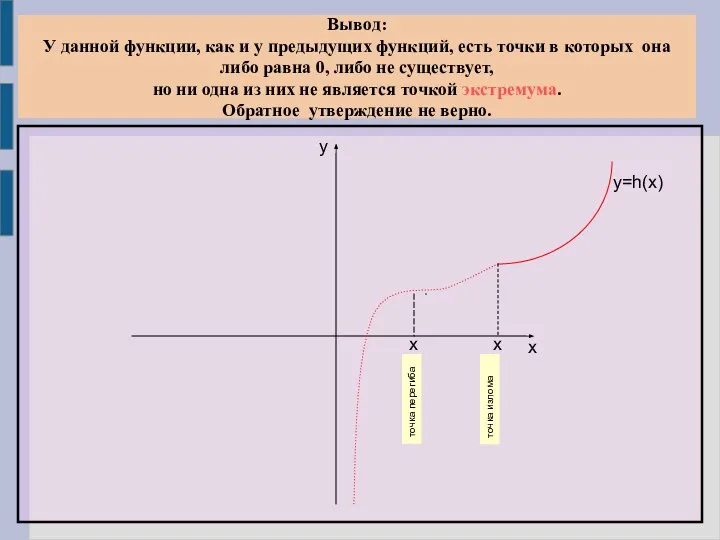
Вывод:
У данной функции, как и у предыдущих функций, есть точки в которых она либо равна 0, либо не существует,
но ни одна из них не является точкой экстремума.
Обратное утверждение не верно.
х1
х2
y=h(x)
x
y
точка излома
точка перегиба

При каких условиях критическая точка будет является точкой экстремума?

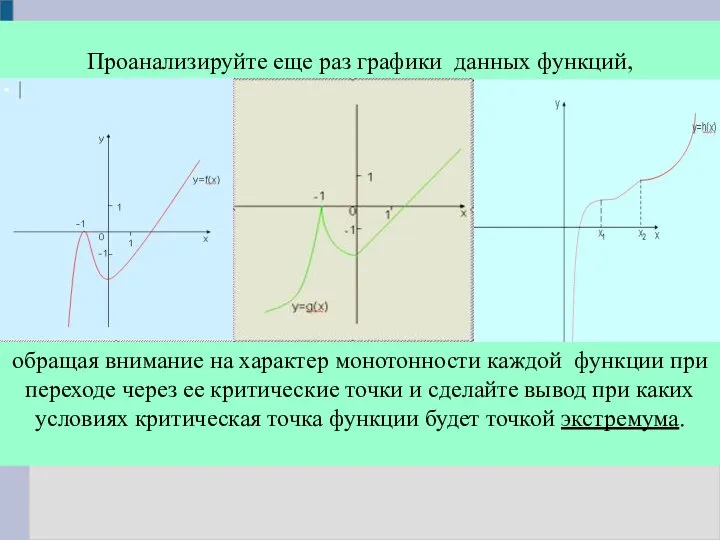
обращая внимание на характер монотонности каждой функции при переходе через ее критические точки и сделайте вывод при каких условиях критическая точка функции будет точкой экстремума.
Проанализируйте еще раз графики данных функций,