Аксиома параллельных прямых

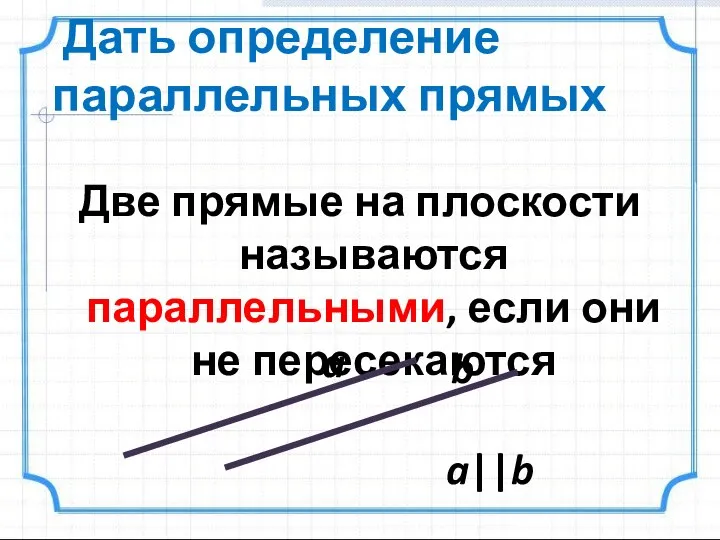
Дать определение параллельных прямых
Две прямые на плоскости называются параллельными, если они не пересекаются
a
b
a||b

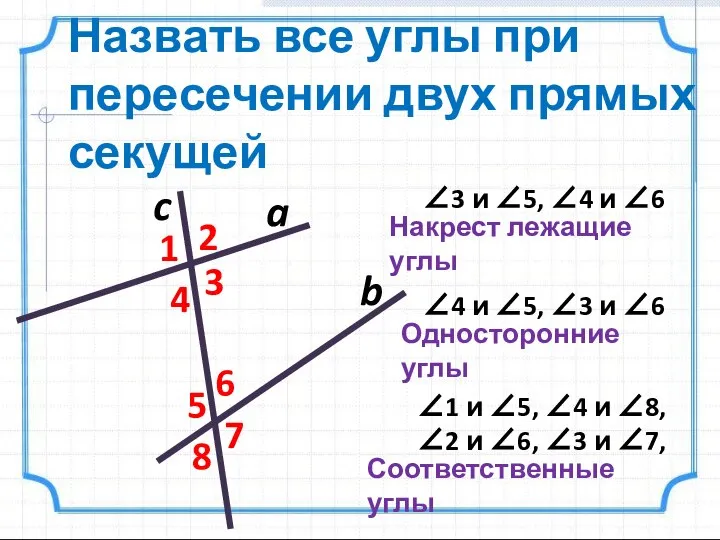
Назвать все углы при пересечении двух прямых секущей
a
b
c
1
2
4
3
5
6
8
7
∠3 и ∠5, ∠4 и ∠6
∠4 и ∠5, ∠3 и ∠6
∠1 и ∠5, ∠4 и ∠8,
∠2 и ∠6, ∠3 и ∠7,
Накрест лежащие углы
Односторонние углы
Соответственные углы

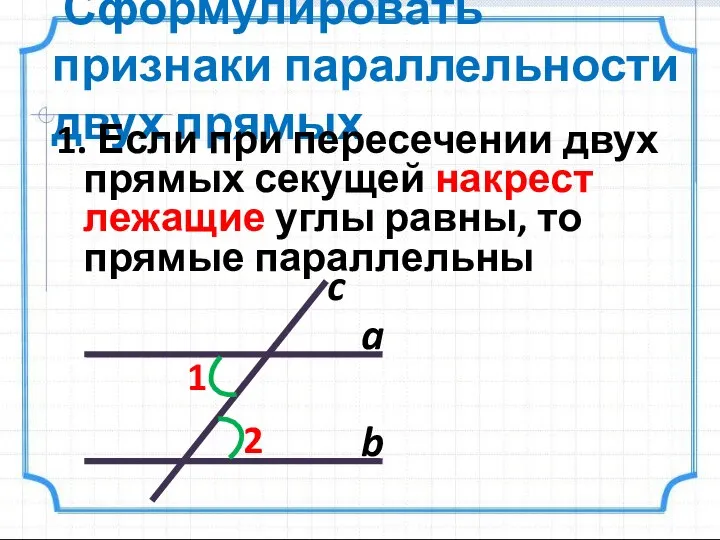
Сформулировать признаки параллельности двух прямых
1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
a
b
c
1
2

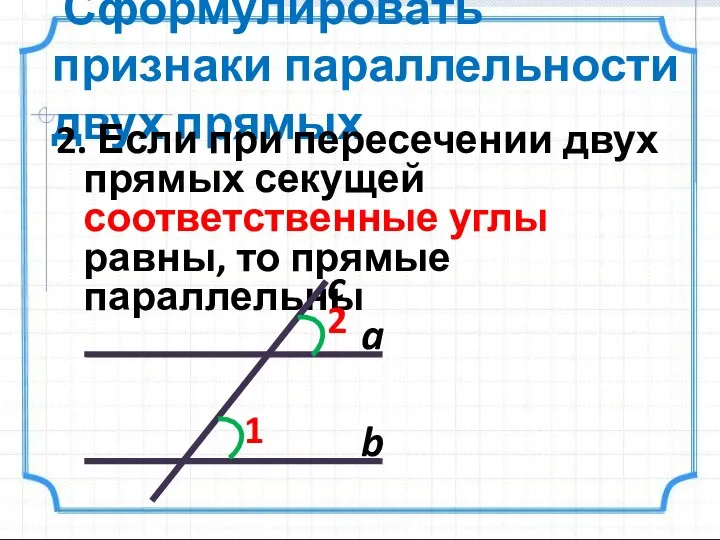
Сформулировать признаки параллельности двух прямых
2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны
a
b
c
1
2

Сформулировать признаки параллельности двух прямых
3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны
a
b
c
1
2
∠1+∠2=180°

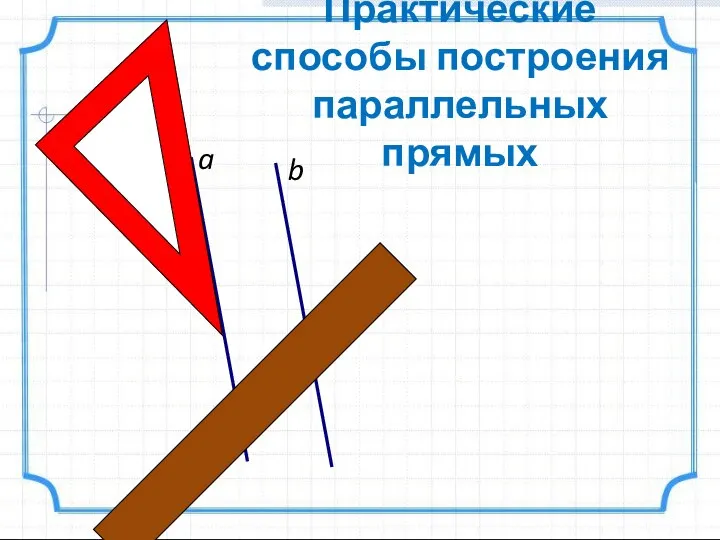
Практические способы построения параллельных прямых
a
M
b

Мы можем решить такую задачу: через точку, не лежащую на прямой, провести прямую, параллельную данной.
А сколько таких прямых можно провести?

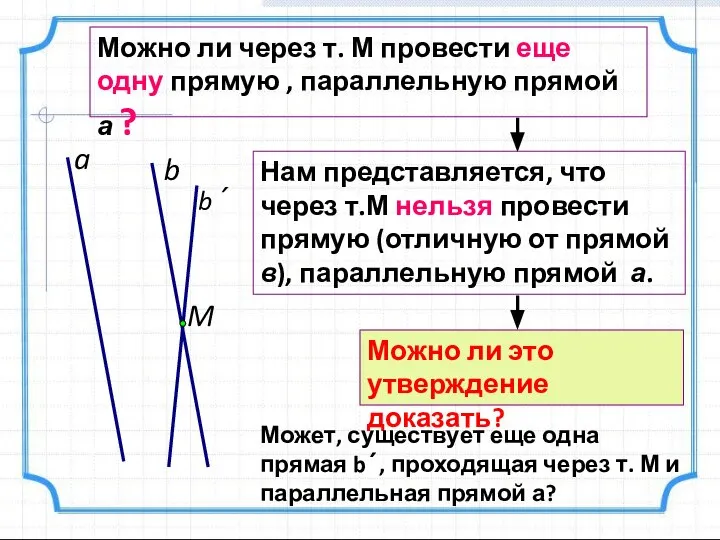
a
M
b
Можно ли через т. М провести еще одну прямую , параллельную прямой а ?
Нам представляется, что через т.М нельзя провести прямую (отличную от прямой в), параллельную прямой а.
Можно ли это утверждение доказать?
Может, существует еще одна прямая b´, проходящая через т. М и параллельная прямой а?
b´

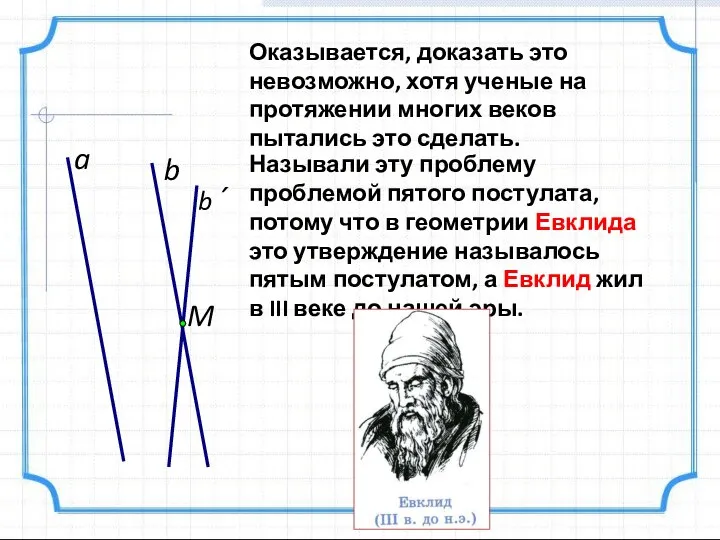
a
M
b
b´
Называли эту проблему проблемой пятого постулата, потому что в геометрии Евклида это утверждение называлось пятым постулатом, а Евклид жил в III веке до нашей эры.
Оказывается, доказать это невозможно, хотя ученые на протяжении многих веков пытались это сделать.

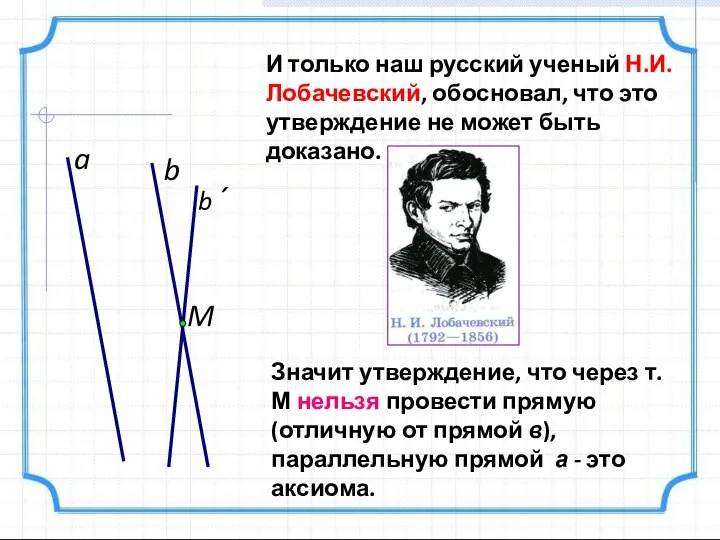
a
M
b
b´
И только наш русский ученый Н.И. Лобачевский, обосновал, что это утверждение не может быть доказано.
Значит утверждение, что через т. М нельзя провести прямую (отличную от прямой в), параллельную прямой а - это аксиома.

В геометрии слово «аксиома» вы слышите впервые, но в жизни оно часто употребляется.
Какое у него значение?

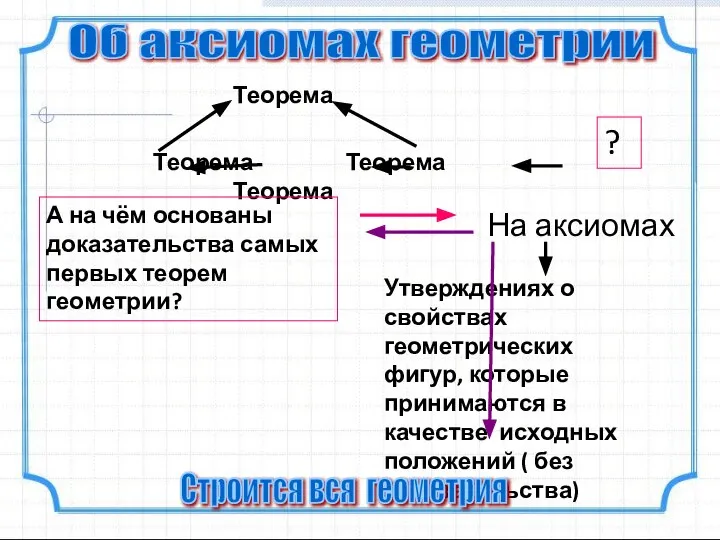
Теорема
Теорема Теорема Теорема
Об аксиомах геометрии
А на чём основаны доказательства самых первых теорем геометрии?
На аксиомах
Утверждениях о свойствах геометрических фигур, которые принимаются в качестве исходных положений ( без доказательства)
?
Строится вся геометрия

Сначала формулируются исходные положения - аксиомы
На их основе, путём логических рассуждений доказываются другие утверждения
Такой подход к построению геометрии зародился в глубокой древности и был изложен в сочинении «Начала» древнегреческого учёного Евклида
365 – 300 гг. до н.э.
Геометрия, изложенная в «Началах», называется евклидовой геометрией
Некоторые из аксиом Евклида (часть из них он называл постулатами) и сейчас используются в геометрии
Слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный».

На самом деле, с аксиомами вы уже встречались в I главе и во II главе

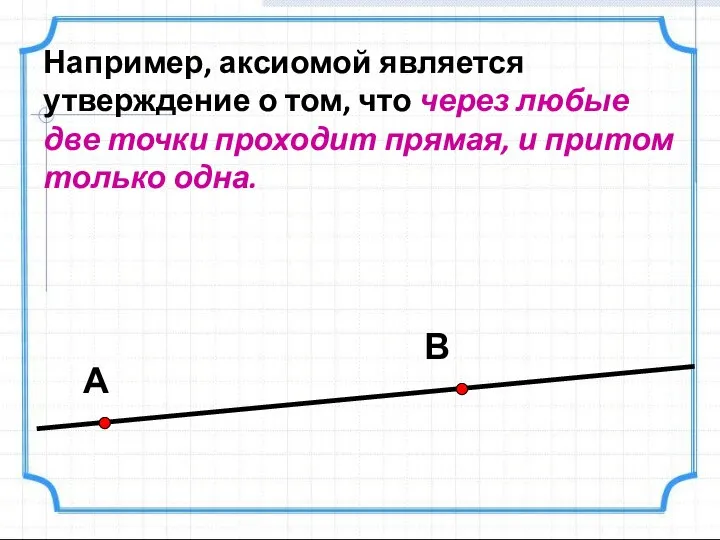
Например, аксиомой является утверждение о том, что через любые две точки проходит прямая, и притом только одна.
А
В

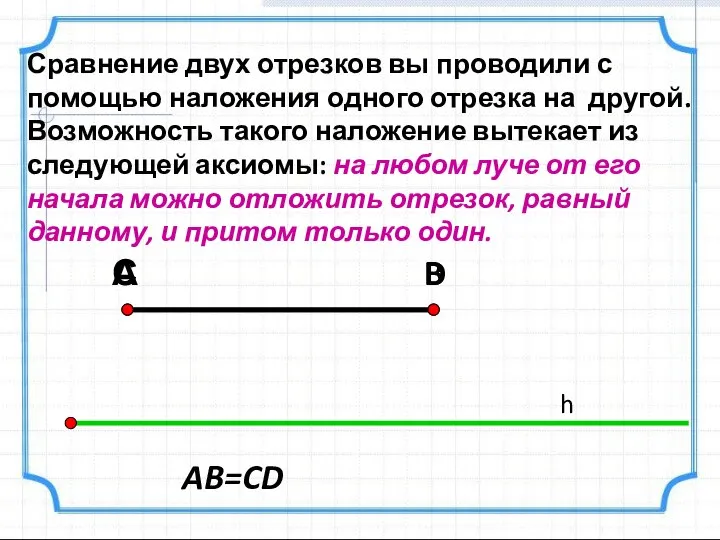
Сравнение двух отрезков вы проводили с помощью наложения одного отрезка на другой. Возможность такого наложение вытекает из следующей аксиомы: на любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
AB=CD

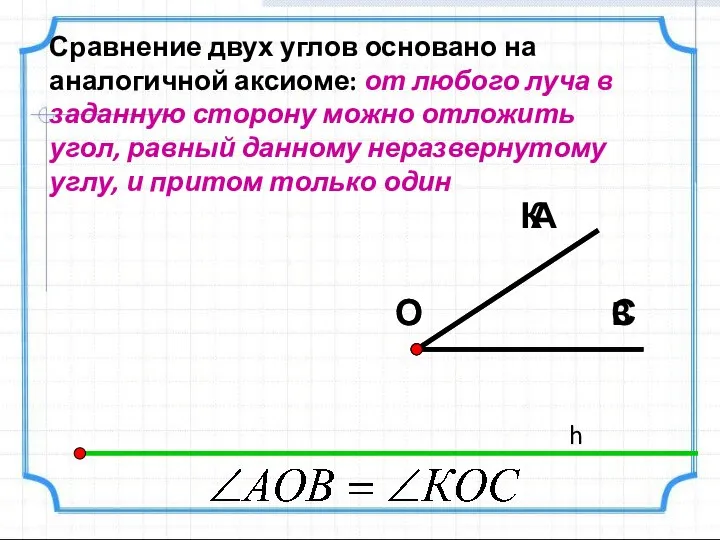
Сравнение двух углов основано на аналогичной аксиоме: от любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один

Обо всех аксиомах планиметрии вы можете прочитать в конце учебника в приложении 1.

Аксиома параллельных прямых:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

У этой аксиомы есть следствия 1о и 2о.
Утверждения, которые выводятся непосредственно из аксиом или теорем, называются следствиями.

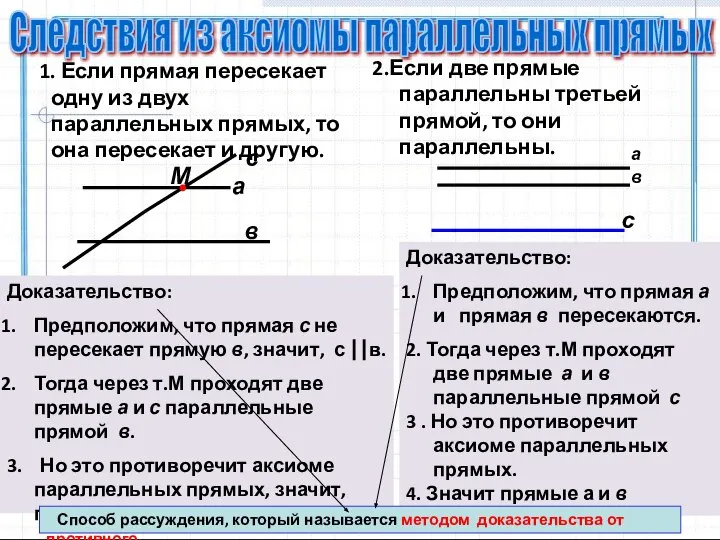
1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
2.Если две прямые параллельны третьей прямой, то они параллельны.
Следствия из аксиомы параллельных прямых
а
в
М
с
Доказательство:
Предположим, что прямая с не пересекает прямую в, значит, с ⎪⎪в.
Тогда через т.М проходят две прямые а и с параллельные прямой в.
3. Но это противоречит аксиоме параллельных прямых, значит, прямая с пересекает прямую в.
а
в
с
Доказательство:
Предположим, что прямая а и прямая в пересекаются.
2. Тогда через т.М проходят две прямые а и в параллельные прямой с
3 . Но это противоречит аксиоме параллельных прямых.
4. Значит прямые а и в параллельны.
Способ рассуждения, который называется методом доказательства от противного

Цель последующих уроков – научиться использовать аксиому параллельных прямых при изучении свойств прямых и при решении задач.