Осевая и центральная симметрия

Что общего на данных рисунках?

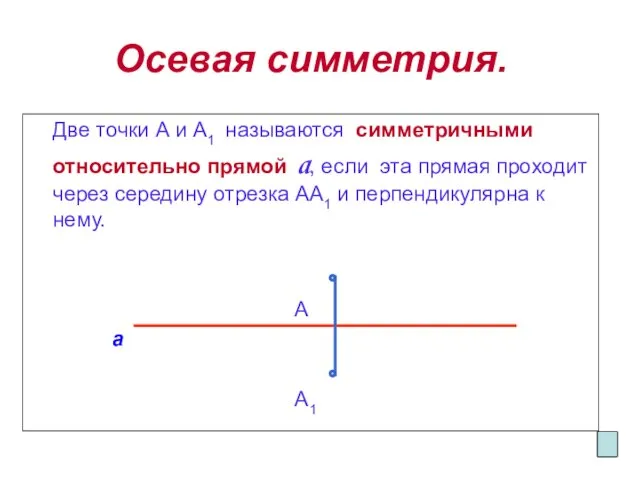
Осевая симметрия.
Две точки А и А1 называются симметричными относительно прямой a, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
А
а
А1

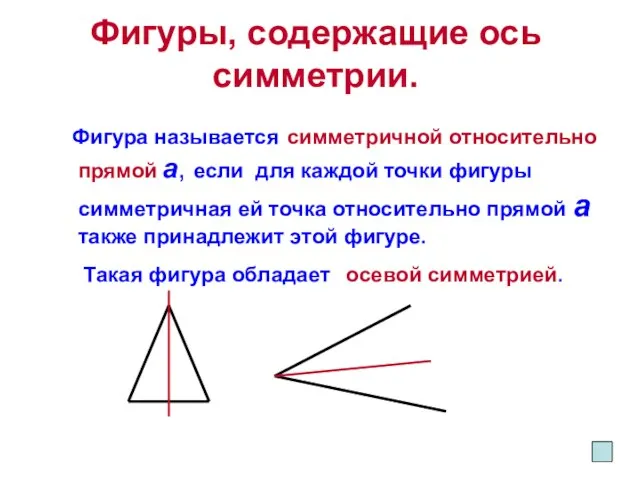
Фигуры, содержащие ось симметрии.
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
Такая фигура обладает осевой симметрией.

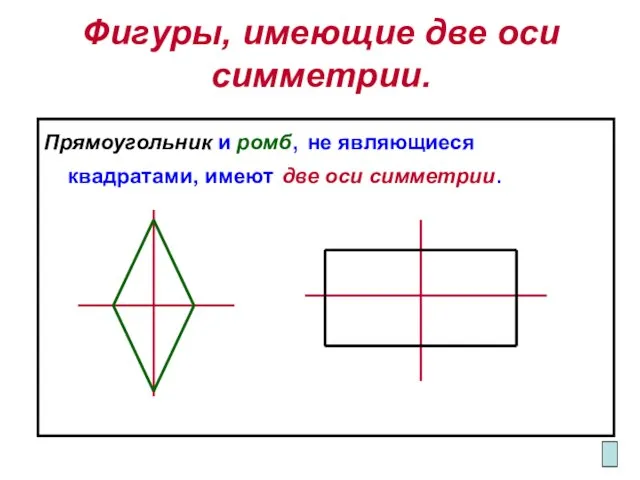
Фигуры, имеющие две оси симметрии.
Прямоугольник и ромб, не являющиеся квадратами, имеют две оси симметрии.

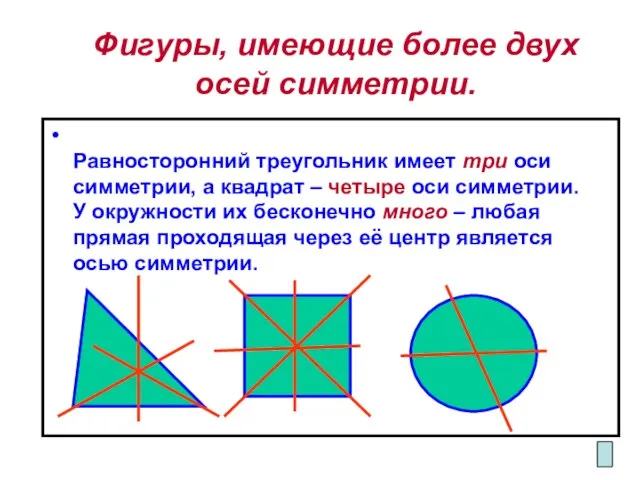
Фигуры, имеющие более двух осей симметрии.
Равносторонний треугольник имеет три оси симметрии, а квадрат – четыре оси симметрии. У окружности их бесконечно много – любая прямая проходящая через её центр является осью симметрии.

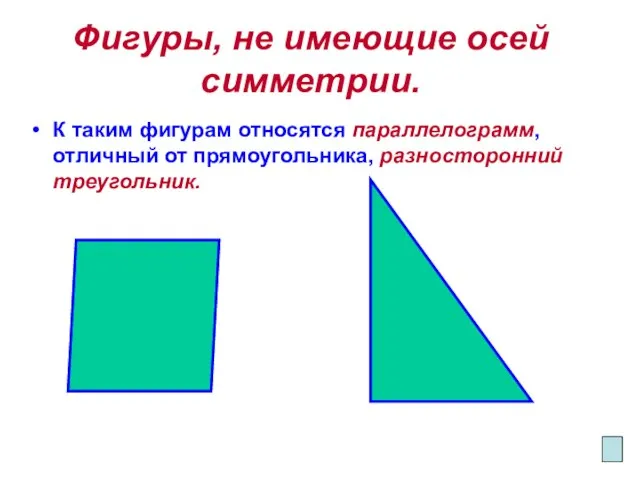
Фигуры, не имеющие осей симметрии.
К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.

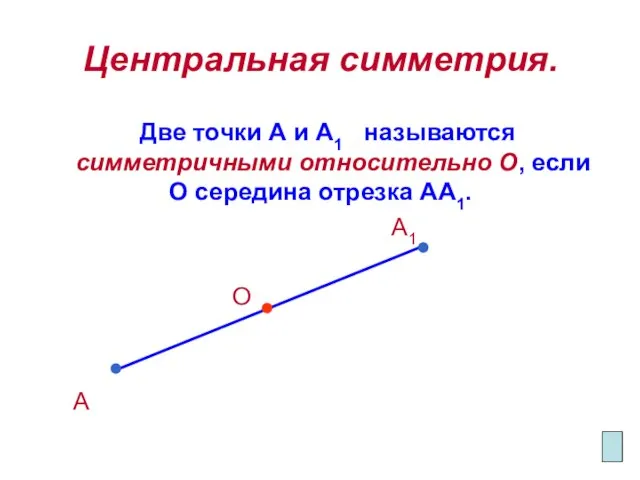
Центральная симметрия.
Две точки А и А1 называются симметричными относительно О, если О середина отрезка АА1.
А1
О
А

Фигура, симметричная, относительно точки.
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии. Такая фигура обладает центральной симметрией.
В
А О
Любая точка прямой является центром симметрии.

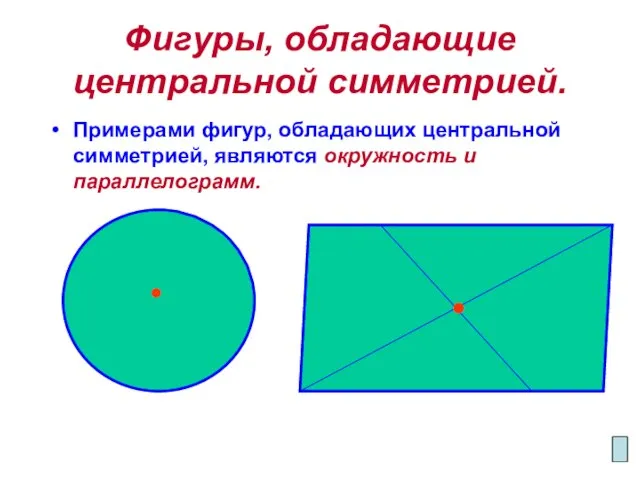
Фигуры, обладающие центральной симметрией.
Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм.

Буквы, имеющие
горизонтальную ось симметрии
В Е Ж З К Н О С Ф Х Э Ю

Буквы, имеющие
вертикальную ось симметрии
А Д Ж Л М Н О П Т Ф Х Ш

Буквы, не имеющие
ось симметрии
Б Г И Р У Ц Ч Я Щ

Симметрия широко распространена в природе

Издавна человек использовал симметрию
в архитектуре

Здание МГУ
им. М. В. Ломоносова
Здание Большого театра в Москве

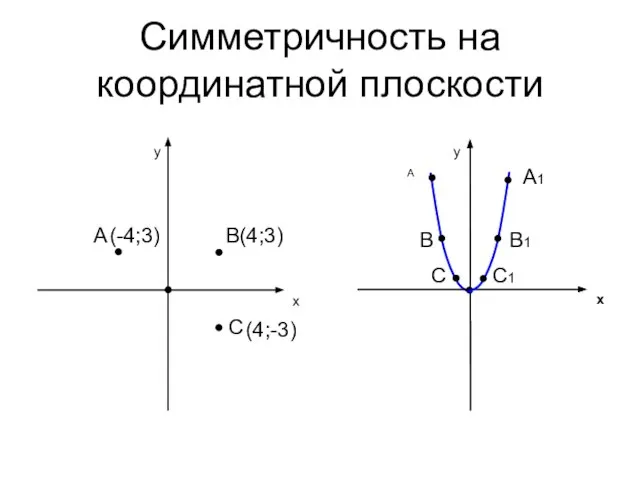
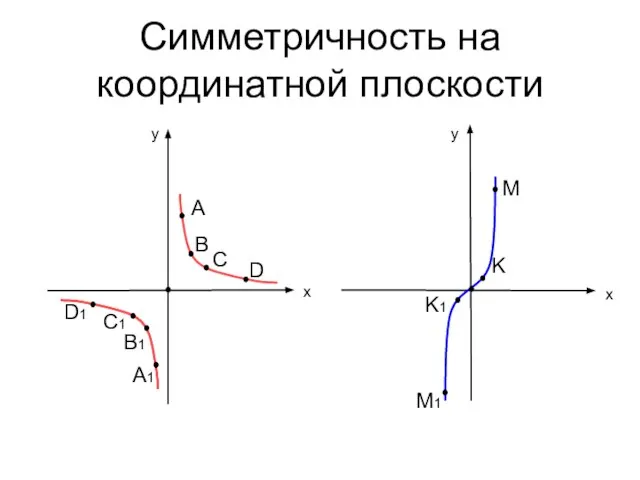
Симметричность на координатной плоскости
y
x
A
B(4;3)
C
y
x
A
A1
B1
B
C
C1
(-4;3)
(4;-3)

Симметричность на координатной плоскости
y
y
x
x
A
B
C
D
A1
B1
C1
D1
M
K
K1
M1

Домашнее задание:
1. 3 п.47 стр.110 (прочитать, выписать и выучить основные определения).
2. Найти симметрию в окружающей среде, привести примеры.
3. Выполнить задание № 417, 418, 421
§

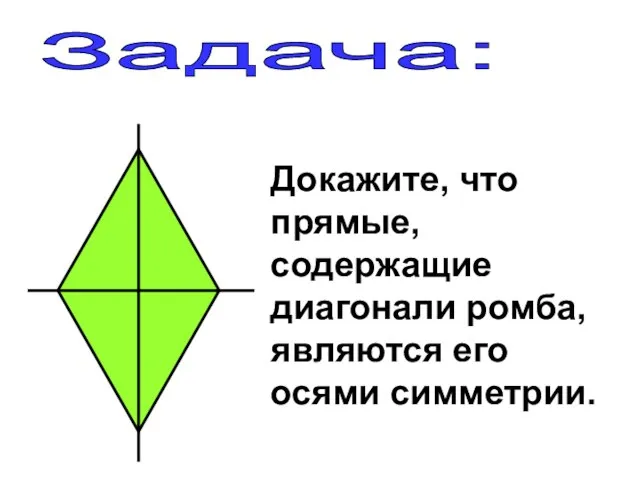
Задача:
Докажите, что прямые, содержащие диагонали ромба, являются его осями симметрии.

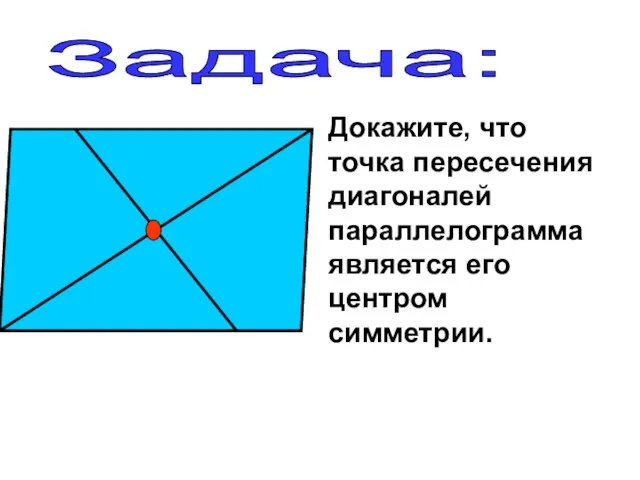
Докажите, что точка пересечения диагоналей параллелограмма является его центром симметрии.
Задача:

1) Сколько осей симметрии имеет фигура?
Вариант 1
Вариант 2
а) одну
б) две
в) четыре
г) множество
а) одну
б) две
в) не имеет
г) четыре

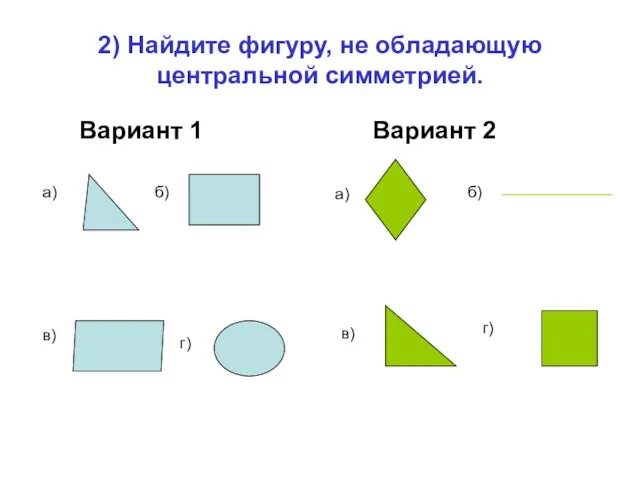
2) Найдите фигуру, не обладающую центральной симметрией.
Вариант 1
Вариант 2
а)
б)
в)
г)
а)
б)
в)
г)

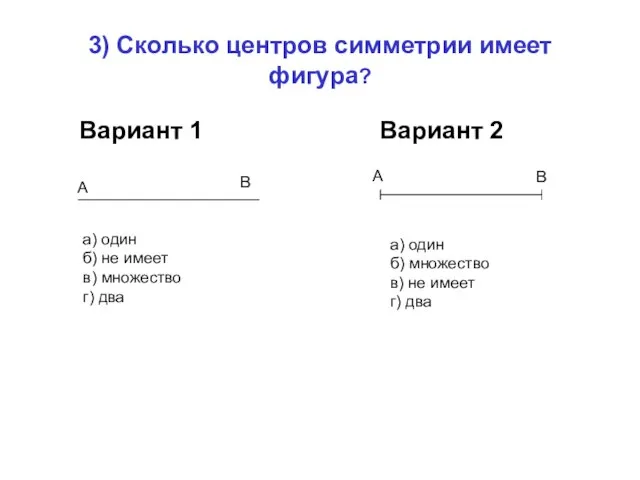
3) Сколько центров симметрии имеет фигура?
Вариант 1
Вариант 2
а) один
б) не имеет
в) множество
г) два
А
В
А
В
а) один
б) множество
в) не имеет
г) два

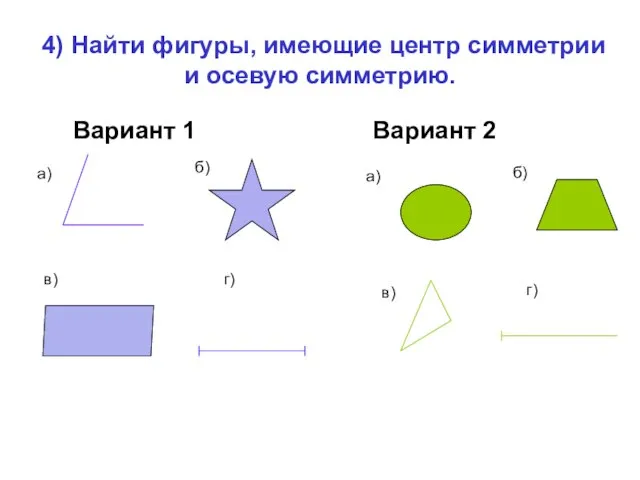
4) Найти фигуры, имеющие центр симметрии и осевую симметрию.
Вариант 1
Вариант 2
а)
б)
в)
г)
а)
б)
в)
г)

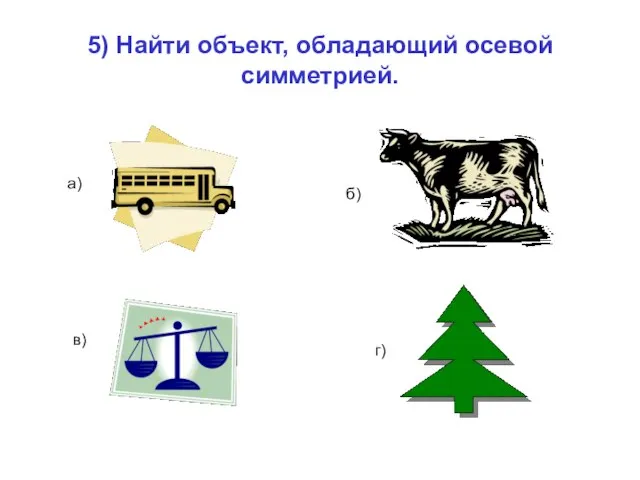
5) Найти объект, обладающий осевой симметрией.
а)
б)
в)
г)

6) Назовите изображение, обладающее центральной симметрией.
а)
б)
в)
г)

7) Найдите объект, обладающий осевой и центральной симметрией
а)
б)
в)
г)

Сколько осей симметрии имеет фигура?