Понятие матрица

Определение. Таблица, составленная из m×n чисел называется матрицей размерности m×n,
m – число строк, n – число столбцов.
m x n – размер матрицы.
Числа аij называются элементами матрицы, i- номер строки, j – номер столбца, на пересечении которых стоит элемент.

Виды матриц
Опр: Две матрицы, имеющие одинаковую размерность m×n, называются матрицами одного типа
1. Если m≠n, то матрица называется прямоугольной.
2. Если m=n, то матрица называется квадратной n-го порядка.

А). Квадратная матрица называется диагональной, если все ее элементы, кроме элементов главной диагонали, равны нулю
Б) Квадратная матрица называется единичной, если элементы диагональной матрицы, стоящие на главной диагонали равны единице.
В) Квадратная матрица называется треугольной, если все элементы матриц, расположенные выше или ниже главной диагонали равны нулю.
.

3. Матрица называется матрицей - строкой, если m=1
4. Матрица называется матрицей - столбцом, если n=1
5. Матрица, все элементы которой равны нулю, называется нулевой матрицей.

Равенство матриц. Две матрицы Аm×n и Bm×n одинаковой размерности равны, если равны соответствующие элементы этих матриц.
Аm×n = Bm×n ⬄ аij = bij

Линейные операции над матрицами.
Линейные операции – это сложение, вычитание, умножение на число.
Сложение и вычитание матриц.
Складывать и вычитать можно только матрицы одинакового размера.
,
Чтобы сложить (или вычесть) две матрицы надо сложить (вычесть) попарно их соответствующие элементы.

:
Задание: Сложите и вычтите матрицы

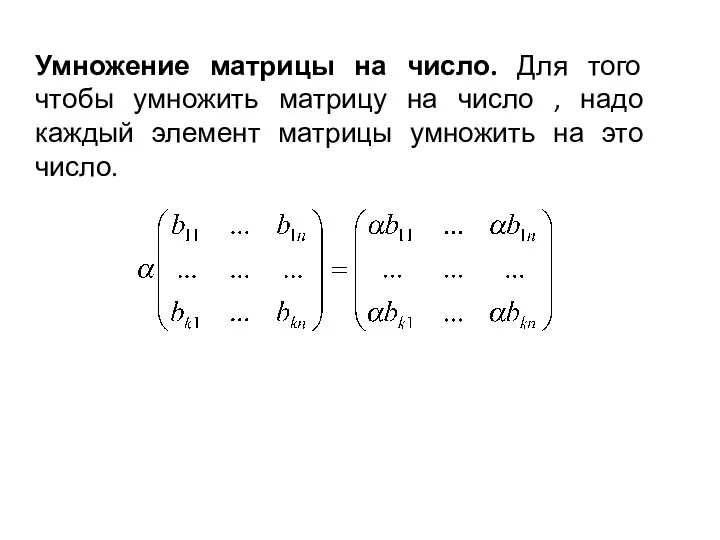
Умножение матрицы на число. Для того чтобы умножить матрицу на число , надо каждый элемент матрицы умножить на это число.

(A+B) +C=A+(B+C)
Линейные операции над матрицами обладают свойствами, схожими со свойствами арифметических операций над действительными числами:
СВОЙСТВА
A+B= B+A
свойства выполнимы для любых матриц А, В, С и любых действительных чисел

Транспонирование матриц.
Операция транспонирования меняет местами строки и столбцы, превращая матрицы размера (kxn) в матрицы (nxk).
Обозначается символом Ат.
Замечание: (Ат)т=А.

Умножение двух матриц.
Чтобы умножить две матрицы, нужно все элементы i-ой строки левой матрицы попарно перемножить с соответствующими элементами j-го столбца правой матрицы, все произведения сложить и полученную сумму записать в новую матрицу на место элемента, стоящего на пересечении i-ой строки и j-го столбца.
По правилу «Строка на столбец».

Замечание 1. Из этого определения следует, что умножать можно матрицы, у которых число столбцов левой матрицы [m×s] равно числу строк правой матрицы [s ×n]. В результате получается матрица размерности m×n.
Замечание 2. Не для всех матриц выполняется свойство, в основном АВ≠ВА . Матрицы, для которых выполняется свойство АВ=ВА называются коммутативными.