Содержание
- 2. Скорость Ускорение Сила Величины, которые характеризуются не только числом, но еще и направлением, называются векторными величинами
- 3. Определение вектора. Геометрически векторы изображаются направленными отрезками. Отрезок, для которого указано, какой из его концов считается
- 4. Если начало вектора – точка А, а его конец – точка В, то вектор обозначается АВ
- 5. Нулевой вектор – точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет
- 6. Коллинеарные векторы. а c b d Два ненулевых вектора называются коллинеарными, если они лежат на одной
- 7. Если векторы и коллинеарные и их лучи направлены в одну сторону, то векторы называются сонаправленными. Обозначаются
- 8. Два вектора называются равными, если они сонаправлены и их длины равны.
- 9. действия над векторами.
- 10. Сложение векторов. Правило треугольника. (правило сложения двух произвольных векторов а и Ь). Отложим от какой-нибудь точки
- 11. Сложение коллинеарных векторов. По этому же правилу складываются и коллинеарные векторы, хотя при их сложении и
- 12. Сложение векторов. Для сложения двух неколлинеарных векторов можно пользоваться также правилом параллелограма, известным из курса планиметрии.
- 13. Свойства сложения векторов. Для любых векторов а, b и с справедливы равенства: а + b =
- 14. Сложение нескольких векторов. Правило многоугольника Сложение нескольких векторов в пространстве выполняется так же, как и на
- 15. Разность векторов. Разностью векторов а и b называется такой вектор, сумма которого с вектором b равна
- 16. Умножение вектора на число. Произведением ненулевого вектора а на число k называется такой вектор b, длина
- 17. Правила умножения вектора на число. Для любых векторов а, b и любых чисел k, f справедливы
- 18. Свойства умножения вектора на число. Отметим, что (-1)а является вектором, противоположным вектору а, т.е. (-1)a =
- 20. Скачать презентацию

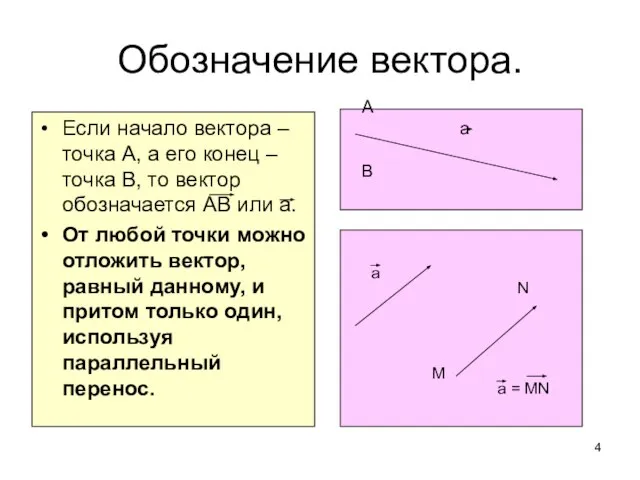

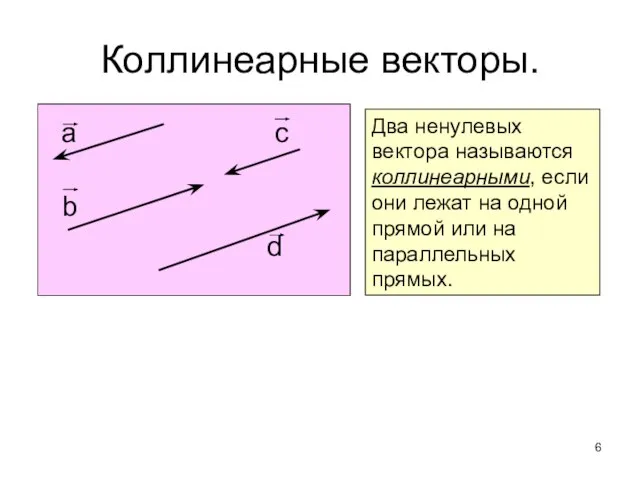

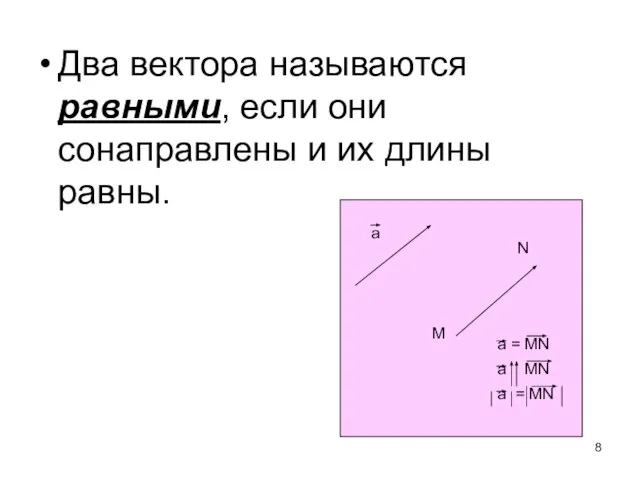

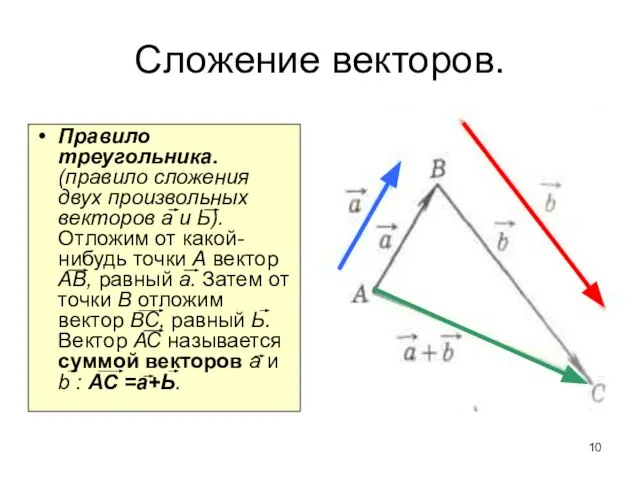
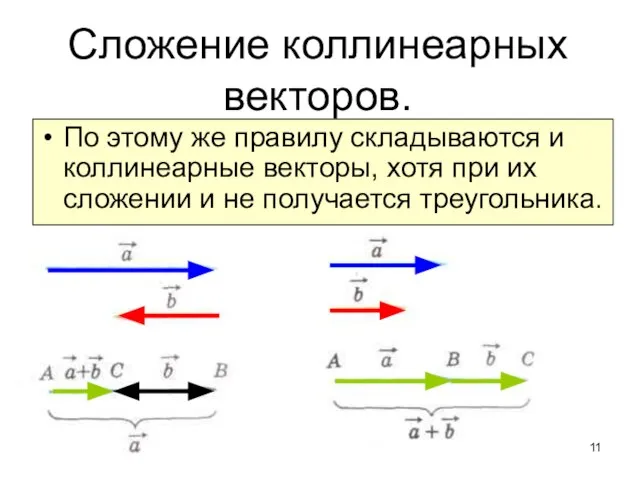
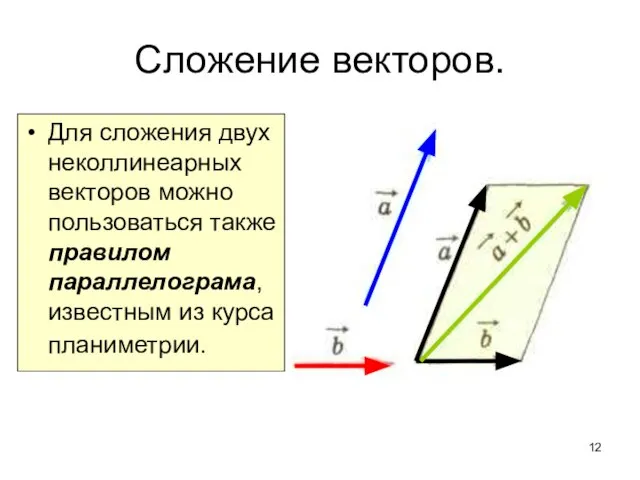

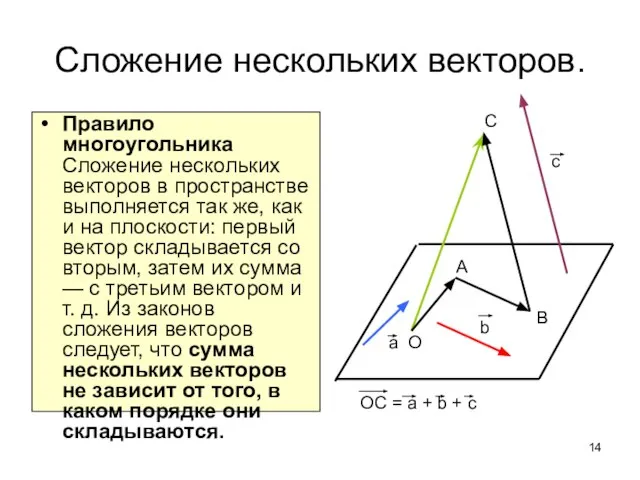




 Таблица сложения
Таблица сложения Как не забыть математику за лето советы методиста
Как не забыть математику за лето советы методиста Устный счет. 6 класс
Устный счет. 6 класс Производные сложной и обратной функций
Производные сложной и обратной функций Определители
Определители Движение подводной лодки. Расчетная работа
Движение подводной лодки. Расчетная работа Числовые головоломки
Числовые головоломки Цель: математическими способами доказать возможный вред курения
Цель: математическими способами доказать возможный вред курения Теорема: Касательная к окружности, перпендикулярная к радиусу,проведенному в точку касания
Теорема: Касательная к окружности, перпендикулярная к радиусу,проведенному в точку касания Основы анализа данных. Регрессионный анализ. (Лекция 6)
Основы анализа данных. Регрессионный анализ. (Лекция 6) Презентация на тему ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
Презентация на тему ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ  Математические модели, постановки задач, алгоритмы обучения, оценки решающих правил
Математические модели, постановки задач, алгоритмы обучения, оценки решающих правил Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Методы решения экстремальных задач
Методы решения экстремальных задач Прямая пропорциональность 7 класс 2012 год
Прямая пропорциональность 7 класс 2012 год Анализ ошибок. Параллелепипеды. 10 класс
Анализ ошибок. Параллелепипеды. 10 класс Задания со спичками
Задания со спичками Функция y = cos x. Ее свойства и график
Функция y = cos x. Ее свойства и график Действия с дробями. Многогранники
Действия с дробями. Многогранники Сумма углов треугольника. Математический диктант
Сумма углов треугольника. Математический диктант Построение и анализ графиков в среде Живая геометрия. 9 класс
Построение и анализ графиков в среде Живая геометрия. 9 класс Математический диктант по теме: Дроби. 6 класс
Математический диктант по теме: Дроби. 6 класс Квадратики 3-5
Квадратики 3-5 Матрицы
Матрицы Numbers and animals
Numbers and animals Олимпийские игры: история, современность и математика
Олимпийские игры: история, современность и математика ГИА - 2016. Открытый банк заданий по математике. Задача №18
ГИА - 2016. Открытый банк заданий по математике. Задача №18 Что такое разложение многочлена на множители
Что такое разложение многочлена на множители