Содержание
- 2. Планиметрия - раздел геометрии, изучающий свойства геометрических фигур на плоскости. Основными фигурами на плоскости являются точка
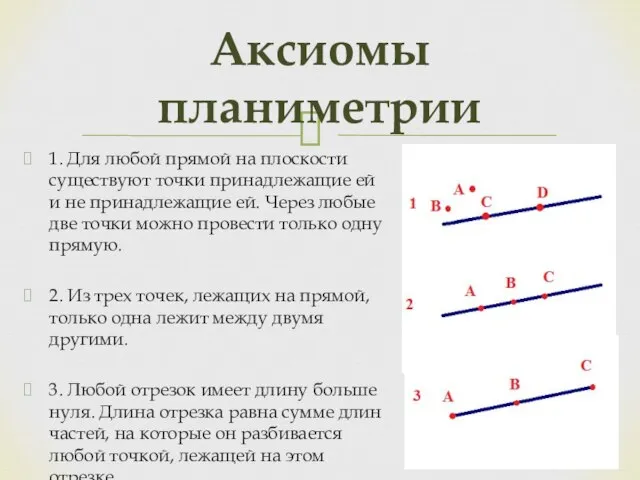
- 3. 1. Для любой прямой на плоскости существуют точки принадлежащие ей и не принадлежащие ей. Через любые
- 4. 4. Любая прямая разбивает плоскость на две полуплоскости. 5. Любой угол имеет определенную градусную меру. Градусная
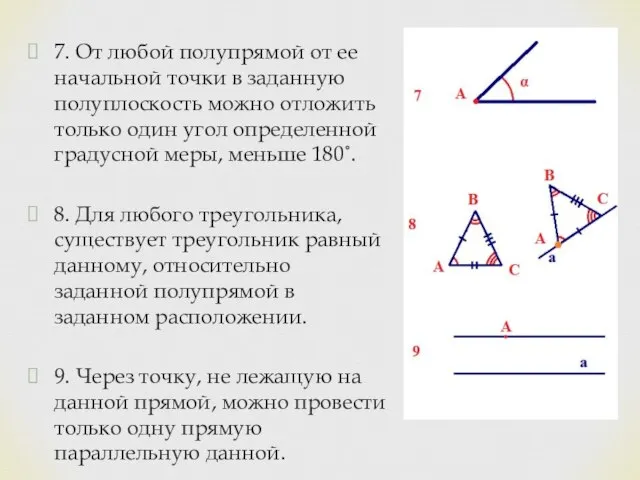
- 5. 7. От любой полупрямой от ее начальной точки в заданную полуплоскость можно отложить только один угол
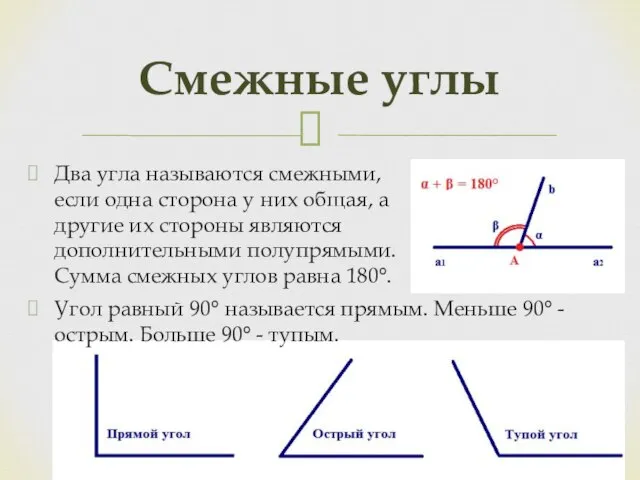
- 6. Два угла называются смежными, если одна сторона у них общая, а другие их стороны являются дополнительными
- 7. Если стороны одного угла являются дополнительными полупрямыми сторон другого угла, то такие углы называются вертикальными. Теорема:
- 8. Если две прямые пересекаются под прямым углом, то такие прямые называются перпендикулярными. Теорема: Через каждую точку
- 9. Теорема: Если две стороны и угол между этими сторонами одного треугольника равны соответственно двум сторонам и
- 10. Возьмем третий треугольник А1В2С2 = АВС. Треугольники А1В1С1 = А1В2С2расположим таким образом, что стороны А1В1 и
- 11. Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Доказательство: 1. Разделим каждую сторону большого
- 12. Основные формулы планиметрии 1. Произвольный треугольник: 2. Прямоугольный треугольник: 3. Равносторонний треугольник: 4. Произвольный выпуклый четырехугольник
- 13. Произвольный треугольник
- 14. Прямоугольный треугольник
- 15. Равносторонний треугольник
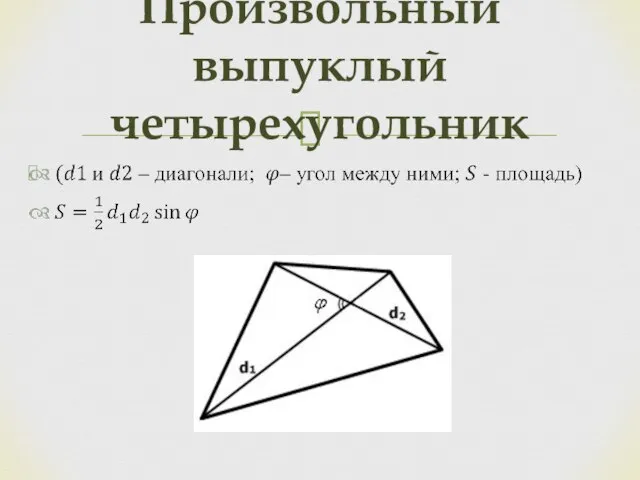
- 16. Произвольный выпуклый четырехугольник
- 17. Параллелограмм
- 18. Ромб
- 19. Прямоугольник и квадрат
- 20. Трапеция
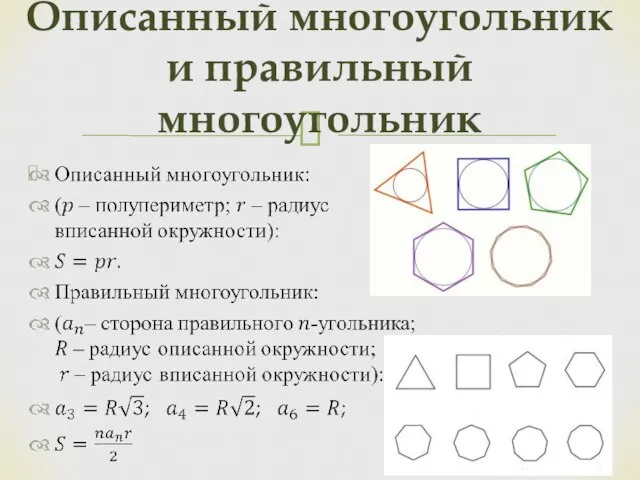
- 21. Описанный многоугольник и правильный многоугольник
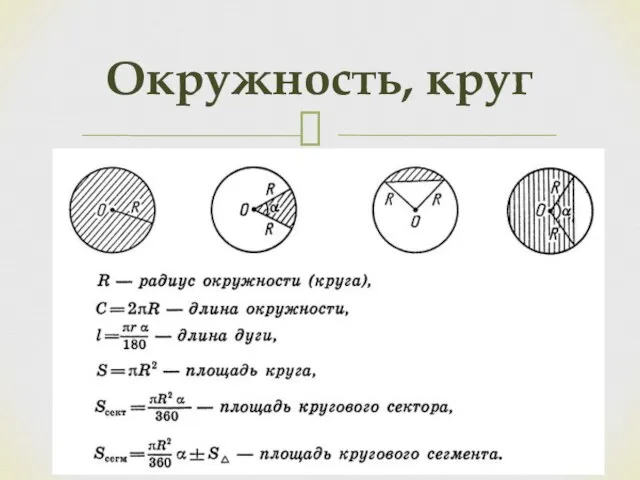
- 22. Окружность, круг
- 24. Скачать презентацию















 Сравнение дробей
Сравнение дробей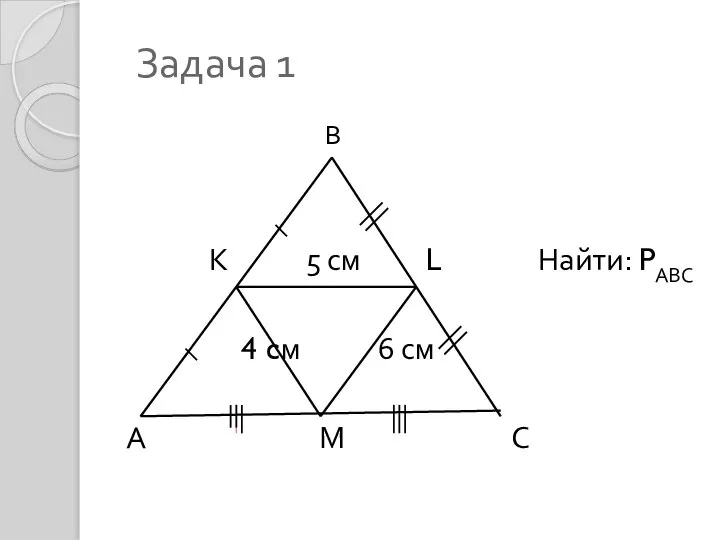 Средняя линия треугольника
Средняя линия треугольника Презентация на тему Софизмы и парадоксы
Презентация на тему Софизмы и парадоксы  Метрология. Лекция 1
Метрология. Лекция 1 Структура. Определение
Структура. Определение Объем наклонной призмы
Объем наклонной призмы Вычисление производной
Вычисление производной Тригонометрическая и показательная форма комплексного числа
Тригонометрическая и показательная форма комплексного числа Режим дня школьника в процентах
Режим дня школьника в процентах Осевая и центральная симметрия
Осевая и центральная симметрия Шар. Элементы шара
Шар. Элементы шара Блок решений mathcad. ПМиПК-8
Блок решений mathcad. ПМиПК-8 Теорема Пифагора
Теорема Пифагора Математическая игра Финансисты. 8 класс
Математическая игра Финансисты. 8 класс Презентация на тему Сложение дробей с одинаковыми знаменателями (4 класс)
Презентация на тему Сложение дробей с одинаковыми знаменателями (4 класс) 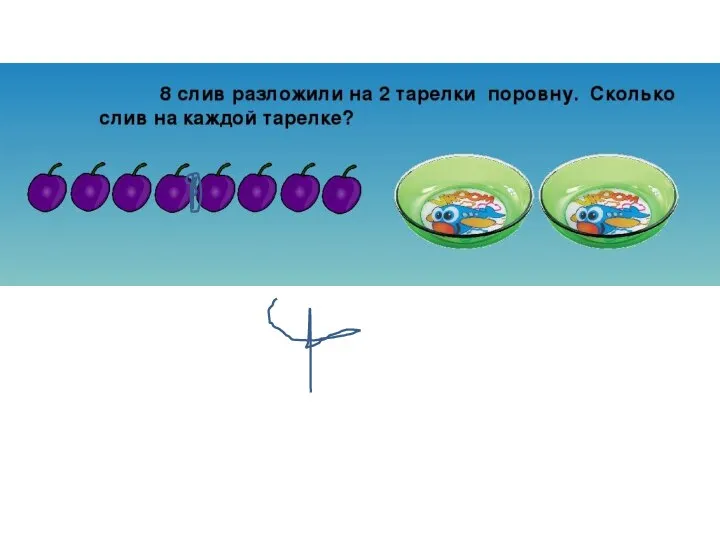 Распредели яблоки по тарелкам поровну
Распредели яблоки по тарелкам поровну Площадь и объём фигуры
Площадь и объём фигуры Графики и диаграммы. Задания
Графики и диаграммы. Задания Блестящая Математика: Математические Игры С Камешками марблс
Блестящая Математика: Математические Игры С Камешками марблс Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника
Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника Заморочки из бочки. Урок-игра Счастливый случай
Заморочки из бочки. Урок-игра Счастливый случай Обучение для выполнения НИР 5 курса. Занятие №2
Обучение для выполнения НИР 5 курса. Занятие №2 Презентация на тему Игра по математике "Счастливый случай"
Презентация на тему Игра по математике "Счастливый случай"  Углы в пространстве
Углы в пространстве Позиционные задачи
Позиционные задачи Число пи вокруг нас
Число пи вокруг нас Разбиение множества
Разбиение множества Криволинейная трапеция
Криволинейная трапеция