Содержание
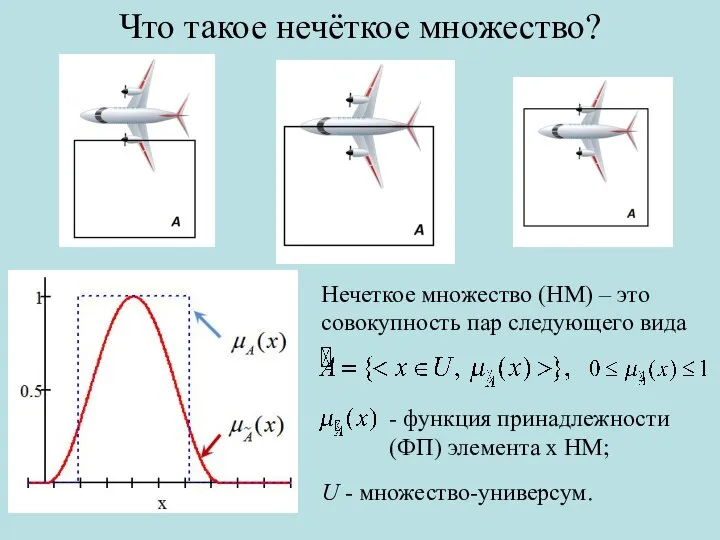
- 2. Что такое нечёткое множество? Нечеткое множество (НМ) – это совокупность пар следующего вида - функция принадлежности
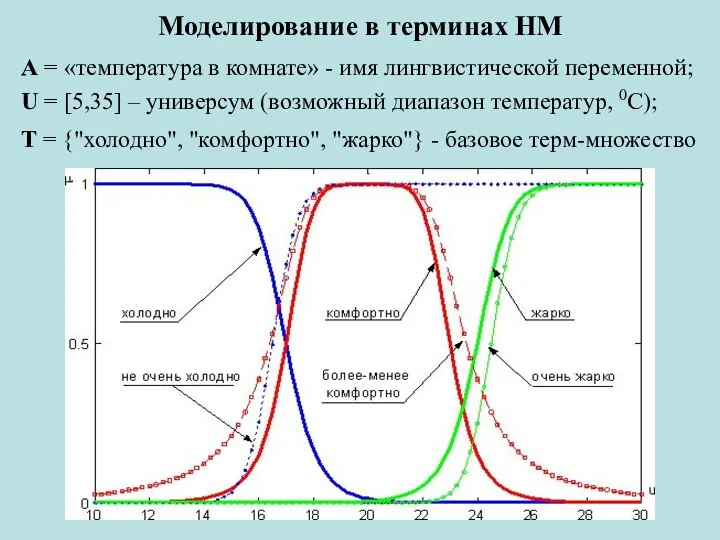
- 3. Моделирование в терминах НМ А = «температура в комнате» - имя лингвистической переменной; U = [5,35]
- 4. Что такое лингвистические модификаторы? Лингвистические модификаторы или «хеджи» (англ. - hedges) определяются как слова, способные изменять
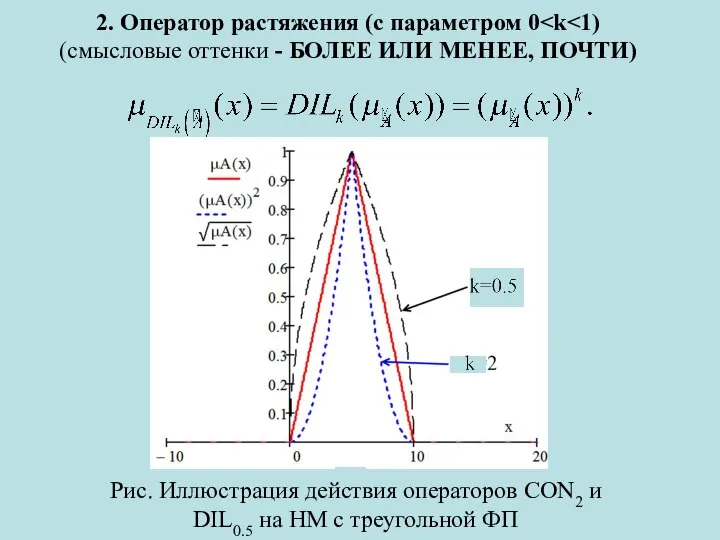
- 5. 2. Оператор растяжения (с параметром 0 (смысловые оттенки - БОЛЕЕ ИЛИ МЕНЕЕ, ПОЧТИ) Рис. Иллюстрация действия
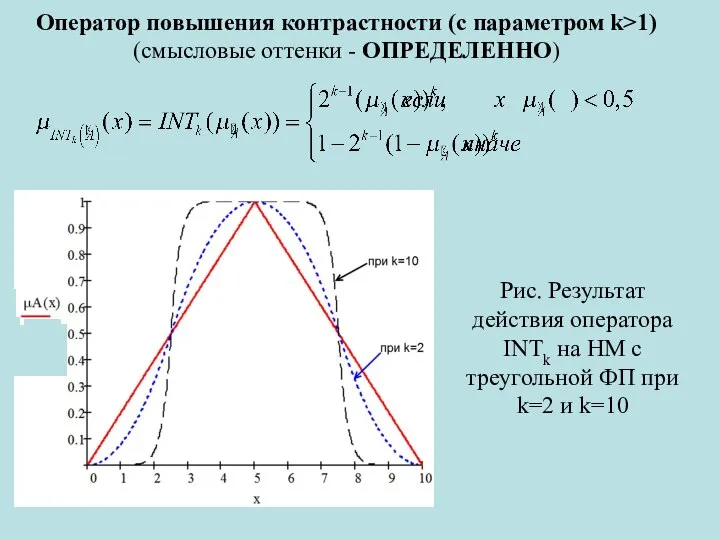
- 6. Оператор повышения контрастности (с параметром k>1) (смысловые оттенки - ОПРЕДЕЛЕННО) Рис. Результат действия оператора INTk на
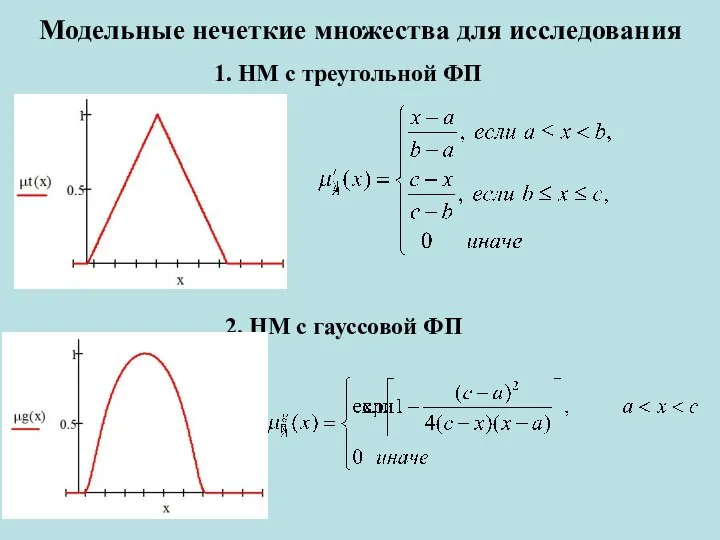
- 7. Модельные нечеткие множества для исследования 1. НМ с треугольной ФП 2. НМ с гауссовой ФП
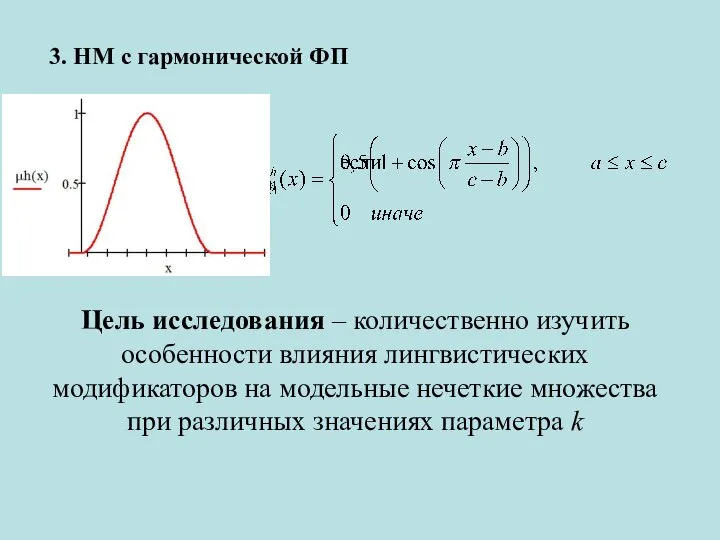
- 8. 3. НМ с гармонической ФП Цель исследования – количественно изучить особенности влияния лингвистических модификаторов на модельные
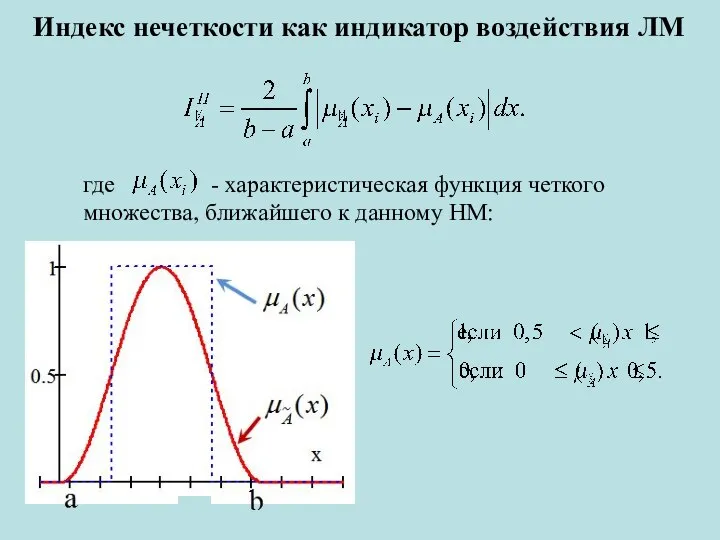
- 9. Индекс нечеткости как индикатор воздействия ЛМ где - характеристическая функция четкого множества, ближайшего к данному НМ:
- 10. В качестве меры эффекта воздействия операторов на НМ при каждом значении параметра k рассчитывался коэффициент относительного
- 11. Моделирование ЛМ в MathCad
- 12. Моделирование ЛМ в MathCad
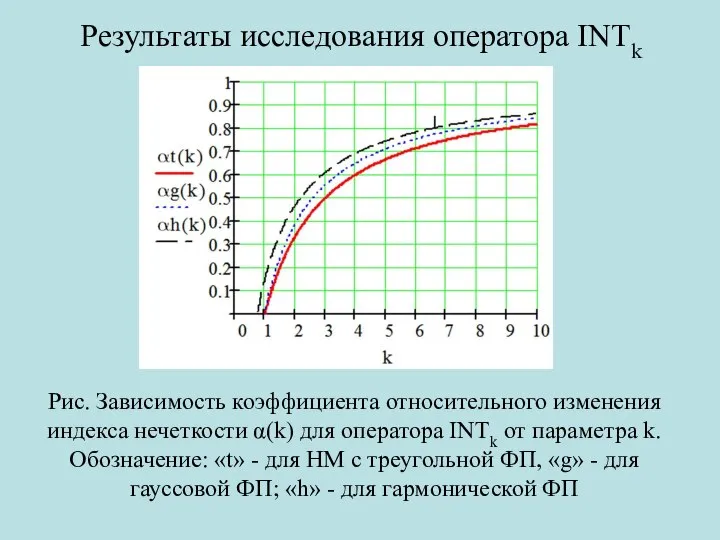
- 13. Результаты исследования оператора INTk Рис. Зависимость коэффициента относительного изменения индекса нечеткости α(k) для оператора INTk от
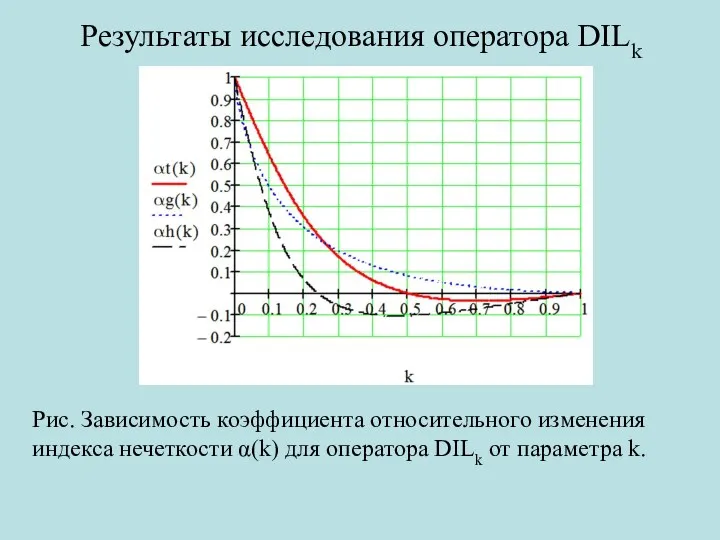
- 14. Результаты исследования оператора DILk Рис. Зависимость коэффициента относительного изменения индекса нечеткости α(k) для оператора DILk от
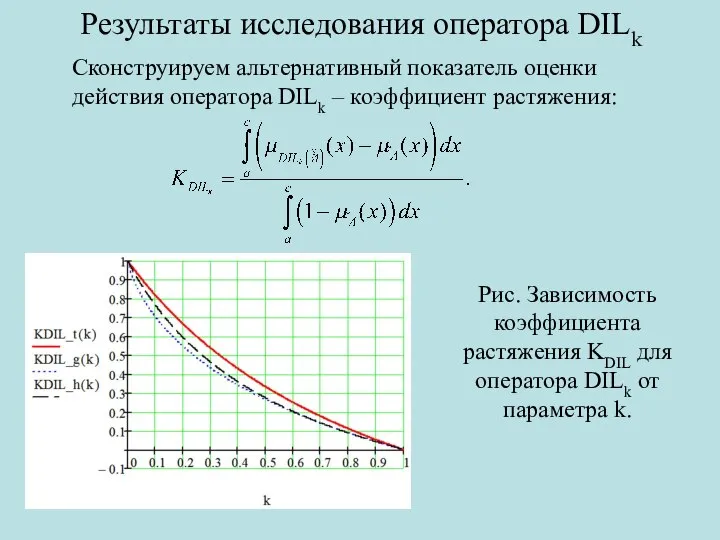
- 15. Результаты исследования оператора DILk Сконструируем альтернативный показатель оценки действия оператора DILk – коэффициент растяжения: Рис. Зависимость
- 17. Скачать презентацию




 Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов
Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов Решение задач. 1 класс
Решение задач. 1 класс Рациональные уравнения
Рациональные уравнения Признаки параллельности прямых
Признаки параллельности прямых Интегрированный урок в 7 классе Грамотная геометрия - геометрия + русский язык
Интегрированный урок в 7 классе Грамотная геометрия - геометрия + русский язык Интегрированный урок алгебры и экономики. 7 класс
Интегрированный урок алгебры и экономики. 7 класс Веселые примеры
Веселые примеры Использование логических операций в теории множеств. Инверсия
Использование логических операций в теории множеств. Инверсия Автор: Стребкова Виктория Ученица 5 класса
Автор: Стребкова Виктория Ученица 5 класса Многочлены над числовыми полями
Многочлены над числовыми полями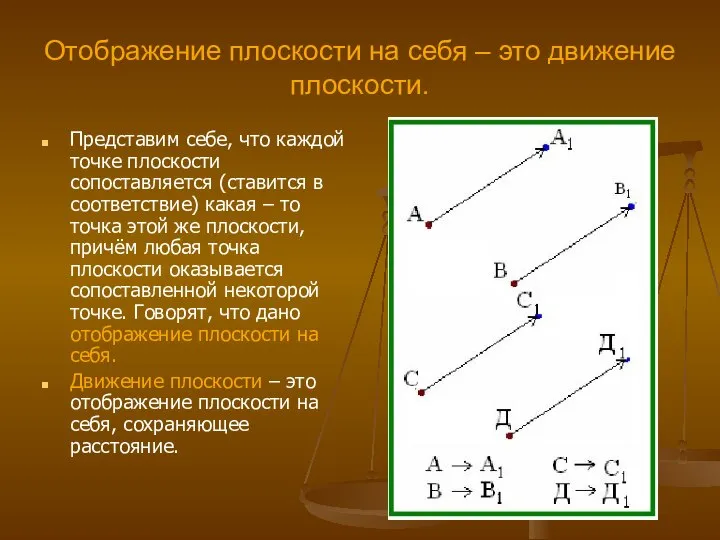 Геометрические преобразования плоскости
Геометрические преобразования плоскости Урок математики в 1 классе
Урок математики в 1 классе Приемы вычитания с переходом через разряд вида 35 - 7
Приемы вычитания с переходом через разряд вида 35 - 7 Числовые выражения
Числовые выражения Множество. Элемент множества
Множество. Элемент множества Литература
Литература Стереометрия. Многогранники
Стереометрия. Многогранники Приёмы умножения числа 2
Приёмы умножения числа 2 Невозможный треугольник
Невозможный треугольник Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)
Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)  Этапы моделирования
Этапы моделирования Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Обыкновенные дроби
Обыкновенные дроби Задачи и примеры. 1 класс
Задачи и примеры. 1 класс Понятия длиннее, короче, одинаковые по длине
Понятия длиннее, короче, одинаковые по длине Тест Смешанные числа
Тест Смешанные числа Усный счет
Усный счет Презентация на тему Буквенные выражения (2 класс)
Презентация на тему Буквенные выражения (2 класс)