первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила.
Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.














 Нефть. Добыча, переработка, использование. Задачи на нахождение объёма цилиндра. Работа с формулами в таблице Excel
Нефть. Добыча, переработка, использование. Задачи на нахождение объёма цилиндра. Работа с формулами в таблице Excel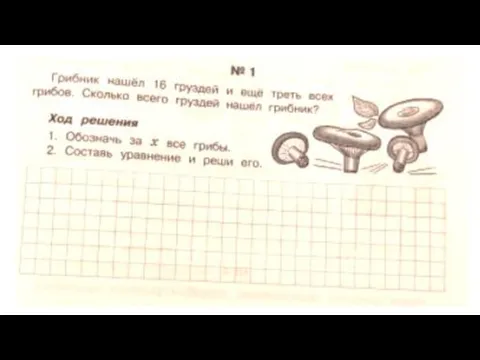 Олимпиадная математика
Олимпиадная математика Цифровая азбука
Цифровая азбука Основные теоремы о дифференцируемых функциях
Основные теоремы о дифференцируемых функциях Краткая история появления и развития пределов
Краткая история появления и развития пределов С чего начать подготовку к ЕГЭ по профильной математике
С чего начать подготовку к ЕГЭ по профильной математике Признаки параллелограмма
Признаки параллелограмма Расчет центральной предельной теоремы
Расчет центральной предельной теоремы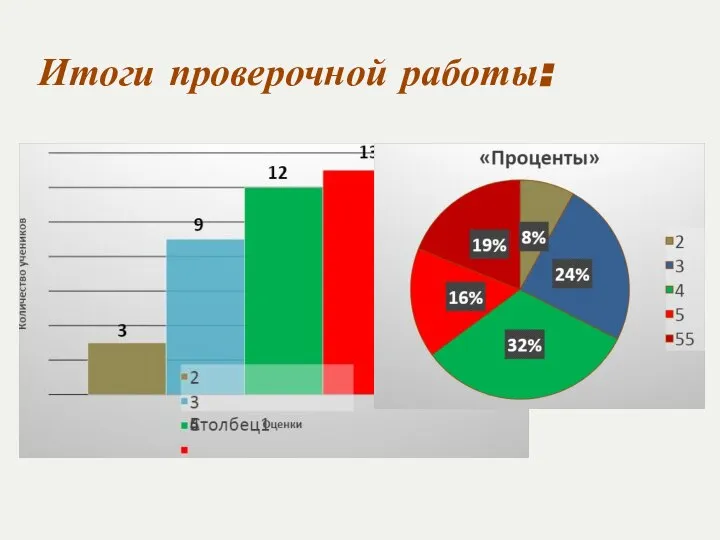 Вертикальные углы
Вертикальные углы Задачки от жителей Солнечного города. 1 класс
Задачки от жителей Солнечного города. 1 класс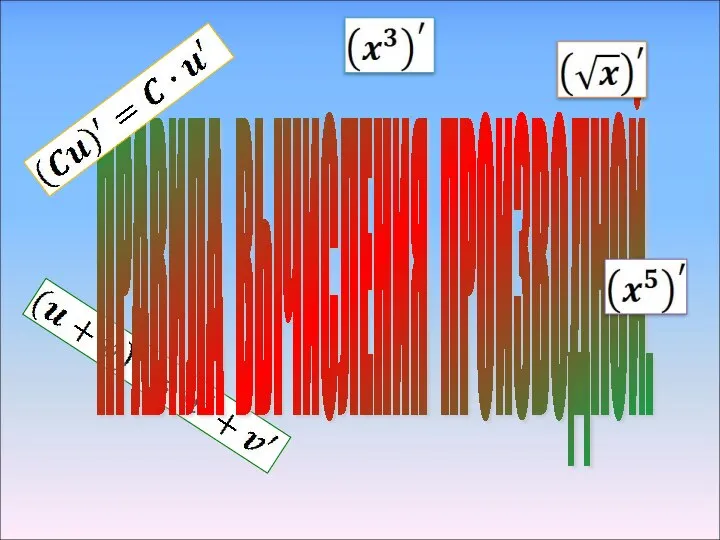 Правила вычисления производной
Правила вычисления производной Математика в профессии строителя
Математика в профессии строителя Комплексные числа
Комплексные числа Площади фигур
Площади фигур Признаки параллельных прямых
Признаки параллельных прямых Решение задач на концентрацию при подготовке к ГИА
Решение задач на концентрацию при подготовке к ГИА Определение куба
Определение куба Системы уравнений
Системы уравнений Дифференциальные уравнения. Лекция
Дифференциальные уравнения. Лекция Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс
Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс Мастер-класс в рамках игры физико-математические забавы
Мастер-класс в рамках игры физико-математические забавы График равномерного движения
График равномерного движения Обработка данных. Задачи локального и глобального интерполирования
Обработка данных. Задачи локального и глобального интерполирования Задачи, обратные данной
Задачи, обратные данной Презентация на тему Прямая и обратная пропорциональность Линейная функция
Презентация на тему Прямая и обратная пропорциональность Линейная функция  Комбинаторика. 11 класс
Комбинаторика. 11 класс Задачи на построение сечений
Задачи на построение сечений Характеристика структуры и содержания экзаменационной работы
Характеристика структуры и содержания экзаменационной работы