Слайд 2«Счет и вычисления – основа порядка в голове»
Иоганн Генрих Песталоцци
Числа играют

огромную роль в нашей жизни. Вычисления нам просто жизненно необходимы. Но как тяжело иногда они нам даются!
Способы устных вычислений - разнообразные. Знание приёмов быстрого счёта позволяет найти рациональный способ решения, экономит время, развивает логическое мышление, тренирует память.
Слайд 3
Актуальность темы заключается в том, что быстрый счёт помогает людям в повседневной жизни, а ученикам на «отлично»

заниматься по математике.
Цели исследовательской работы: изучить методы и приёмы быстрого счёта
Слайд 4Суммируем однозначные числа
Сложения однозначных чисел с переходом через десяток.
Предположим, вам нужно сложить

7 и 8.
1)Посчитайте, сколько семёрке не хватает до десяти: 10 − 7 = 3
2)Разложите восьмёрку на сумму трёх и второй части: 8 = 3 + 5.
3)Добавьте вторую часть к десяти: 10 + 5 = 15.
Тот же приём «опоры на десятку» используйте при суммировании однозначных чисел с двузначными, трёхзначными и так далее
Слайд 5
Суммируем многозначные числа
Основной принцип — разбить слагаемые числа на разряды

(тысячи, сотни, десятки, единицы) и суммировать между собой одинаковые, начиная с самых крупных.
Допустим, вы прибавляете 1 574 к 689.
1 574 раскладывается на четыре разряда: 1 000, 500, 70 и 4. 689 — на три: 600, 80 и 9.
Теперь суммируем: тысячи с тысячами (1 000 + 0 = 1 000), сотни с сотнями (500 + 600 = 1 100), десятки с десятками (70 + 80 = 150), единицы с единицами (4 + 9 = 13).
Группируем числа так, как нам удобно, и складываем то, что получилось: (1 000 + 1 100) + (150 + 13) = 2 100 + 163 = 2 263.
Основная сложность — удержать в голове все промежуточные результаты. Упражняясь в таком счёте, вы заодно тренируете память.
Слайд 6Как научиться вычитать в уме
Вычитаем однозначные числа
Оттачиваем навык вычитания однозначного числа с

переходом через десяток.
Предположим, вы хотите отнять 8 от 35.
Представьте 35 в виде суммы 30 + 5.
Из 5 вычесть 8 нельзя, поэтому раскладываем 8 на сумму 5 + 3.
Вычтем 5 из 35 и получим 30. Затем отнимем от 30 оставшуюся тройку:
30 − 3 = 27.
Слайд 7Вычитаем многозначные числа
В отличие от сложения, при вычитании многозначных чисел на разряды

нужно разбивать только то, которое вы отнимаете.
Например, вас просят отнять 347 от 932.
Число 347 состоит из трёх разрядных частей: 300 + 40 + 7.
Сначала вычитаем сотни: 932 − 300 = 632.
Переходим к десяткам: 632 − 40. Для удобства 40 можно представить в виде суммы 30 + 10. Сперва вычтем 30 и получим 632 − 30 = 602. Теперь отнимем от 602 оставшиеся 10 и получим 592.
Осталось разобраться с единицами, используя всё ту же «опору на десятку». Сперва вычитаем из 592 двойку: 592 − 2 = 590. А затем то, что осталось от семёрки: 7 − 2 = 5. Получаем: 590 − 5 = 585.
Слайд 8Умножаем двузначные числа
Тут уже рука сама тянется к калькулятору или хотя бы

к бумаге и ручке, чтобы воспользоваться старым добрым умножением в столбик. Хотя ничего сверхсложного в этой операции нет. Просто нужно немного потренировать краткосрочную память.
Попробуем умножить 47 на 32, разбив процесс на несколько шагов.
47 × 32 — это то же, что и 47 × (30 + 2) или 47 × 30 + 47 × 2.
Сначала умножим 47 на 30.
Проще некуда: 47 × 3 = 40 × 3 + 7 × 3 = 120 + 21 = 141. Приписываем справа нолик и получаем: 1 410.
Поехали дальше: 47 × 2 = 40 × 2 + 7 × 2 = 80 + 14 = 94.
Осталось сложить результаты: 1 410 + 94 = 1 500 + 4 = 1 504.
Слайд 9
Упрощаем умножение
Кроме общих правил, есть несколько лайфхаков, облегчающих умножение на определённые

однозначные числа.
Умножение на 4
Можно умножить многозначное число на 2, а потом снова на 2.
Пример: 146 × 4 = (146 × 2) × 2 = (200 + 80 + 12) × 2 = 292 × 2 = 400 + 180 + 4 = 584.
Умножение на 5
Умножьте исходное число на 10, а потом разделите на 2.
Пример: 489 × 5 = 4 890 / 2 = 2 445.
Умножение на 9
Умножьте на 10, а затем отнимите от результата исходное число.
Пример: 573 × 9 = 5 730 − 573 = 5 730 − (500 + 70 + 3) = 5 230 − (30 + 40) − 3 =
5 200 − 40 − 3 = 5 160 − 3 = 5 157.
Слайд 10Делим на однозначное число
Для этого разбиваем исходное многозначное число на удобные части,

которые точно будут делиться на наше однозначное.
Попробуем разделить 2 436 на 7.
Выделим из 2 436 наибольшую часть, которая нацело разделится на 7.
В нашем случае это 2 100. Получаем (2 100 + 336) / 7.
Продолжаем в том же духе, только теперь с числом 336. Очевидно, что
на 7 разделится 280. А в остатке будет 56.
Теперь делим каждую часть на 7: (2 100 + 280 + 56) / 7 = 300 + 40 + 8 = 348.









 Прямоугольник. Квадрат. Периметр многоугольника
Прямоугольник. Квадрат. Периметр многоугольника Таблица умножения. Урок математики. 3 класс
Таблица умножения. Урок математики. 3 класс Линейная алгебра
Линейная алгебра 6a04a5dd-75c3-461b-a240-737df2a5d137
6a04a5dd-75c3-461b-a240-737df2a5d137 Множество значений тригонометрических функций
Множество значений тригонометрических функций Организация исследовательской деятельности учащихся на уроках математики
Организация исследовательской деятельности учащихся на уроках математики Процент
Процент Выполнение плана чертежа в масштабе
Выполнение плана чертежа в масштабе Свойство углов треугольника
Свойство углов треугольника Это полезно знать. Математика в кулинарии
Это полезно знать. Математика в кулинарии Свидание. Личный сайт
Свидание. Личный сайт Презентация на тему Порядок выполнения действий в выражениях со скобками
Презентация на тему Порядок выполнения действий в выражениях со скобками  Построение угла, равного данному
Построение угла, равного данному Морское путешествие
Морское путешествие Арифметический квадратный корень. Задания для устного счета. 8 класс
Арифметический квадратный корень. Задания для устного счета. 8 класс Актуализация знаний
Актуализация знаний Применение теоремы Пифагора
Применение теоремы Пифагора Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка
Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка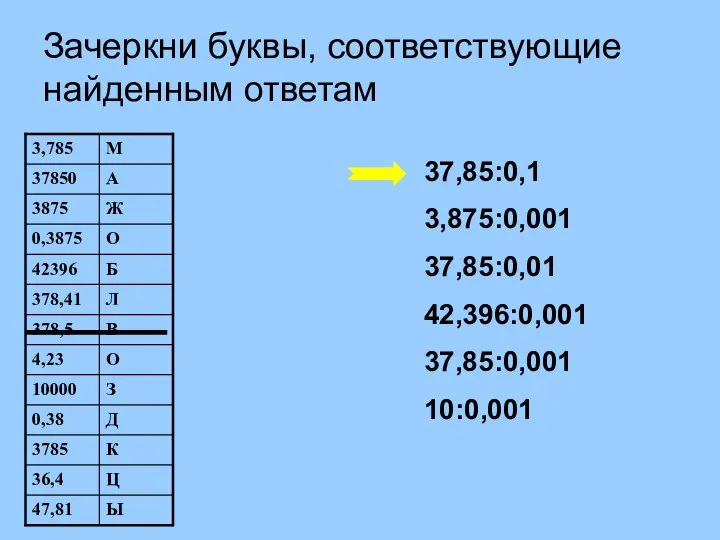 Устная работа (1). Зачеркни буквы, соответствующие найденным ответам
Устная работа (1). Зачеркни буквы, соответствующие найденным ответам Решение задач по теме Равнобедренный треугольник
Решение задач по теме Равнобедренный треугольник Выборка. Обобщение введенных понятий
Выборка. Обобщение введенных понятий Математика вокруг нас. Геометрия на столе с ножницами и без
Математика вокруг нас. Геометрия на столе с ножницами и без Знаки неравенств. Историческая справка
Знаки неравенств. Историческая справка Школа олимпийского резерва. (задача)
Школа олимпийского резерва. (задача) Аксиомы стереометрии
Аксиомы стереометрии Математическая статистика
Математическая статистика Решение задач
Решение задач Презентация на тему Дифференциальные уравнения первого порядка
Презентация на тему Дифференциальные уравнения первого порядка