Содержание
- 2. Логика – наука о формах и законах правильного мышления, ведущего к истине. ГЛАВНАЯ ЗАДАЧА ЛОГИКИ состоит
- 3. Элементы математической логики Пусть F – множество всех высказываний русского языка. A, B, C ... –
- 4. Таблица истинности Логическая операция ИНВЕРСИЯ (операция отрицания) – новое высказывание, которое ложно, когда высказывание истинно и
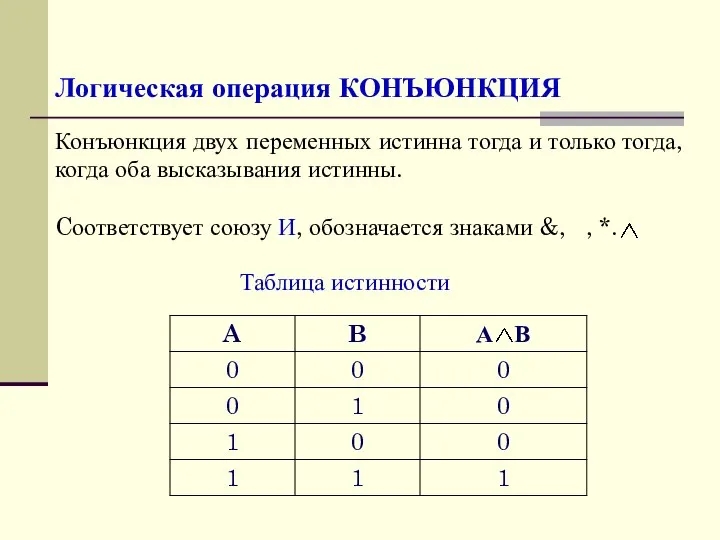
- 5. Логическая операция КОНЪЮНКЦИЯ Конъюнкция двух переменных истинна тогда и только тогда, когда оба высказывания истинны. Cоответствует
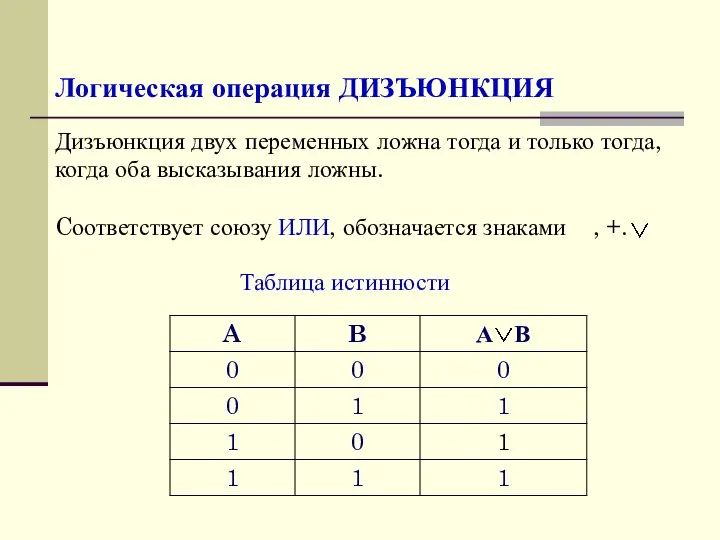
- 6. Логическая операция ДИЗЪЮНКЦИЯ Дизъюнкция двух переменных ложна тогда и только тогда, когда оба высказывания ложны. Cоответствует
- 7. Основные понятия комбинаторики Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и
- 8. Основные понятия комбинаторики Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются
- 9. Основные понятия комбинаторики Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются
- 10. Случайные события и операции над ними Событие называется случайным, если при осуществлении испытания оно может либо
- 11. События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным
- 12. Случайные события и операции над ними События называют несовместными, если появление одного из них исключает появление
- 13. Классическое определение вероятности события Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему
- 14. Основные теоремы и формулы теории вероятности Теорема сложения: вероятность появления одного из двух несовместных событий, безразлично
- 15. Основные теоремы и формулы теории вероятности Теорема умножения: вероятность совместного появления двух событий равна произведению вероятности
- 16. Основные теоремы и формулы теории вероятности Теорема умножения для независимых событий: Событие В называют независимым от
- 18. Скачать презентацию













 Как называются числа при вычитании?
Как называются числа при вычитании? Делители числа. Наибольший общий делитель
Делители числа. Наибольший общий делитель Понятие логарифма
Понятие логарифма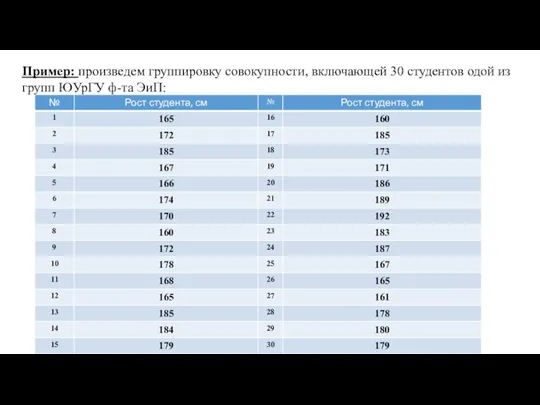 Группировка
Группировка Найди соседей. Дидактическая игра
Найди соседей. Дидактическая игра Тест по теме Окружность
Тест по теме Окружность Алгебраические уравнения
Алгебраические уравнения Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях
Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях Методологическое обеспечение экспериментальных исследований
Методологическое обеспечение экспериментальных исследований О числах
О числах Функция у = √х, ее свойства и график
Функция у = √х, ее свойства и график Координатная плоскость
Координатная плоскость Свойства и графики
Свойства и графики Классы интегрируемых функций
Классы интегрируемых функций Ортодромия и локсодромия
Ортодромия и локсодромия Схемы изонити
Схемы изонити Вероятность события есть количественная мера возможности наступления этого события
Вероятность события есть количественная мера возможности наступления этого события Деление и умножение
Деление и умножение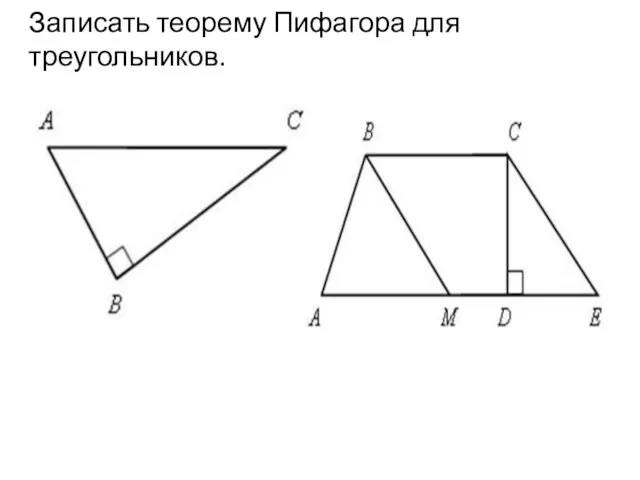 Теорема Пифагора. Урок 24
Теорема Пифагора. Урок 24 Векторный порядок. Дифференциальные операции второго порядка
Векторный порядок. Дифференциальные операции второго порядка Решение уравнений. Математика. 6 класс
Решение уравнений. Математика. 6 класс Задачи на разрезание
Задачи на разрезание Поліноми. Додавання поліномів
Поліноми. Додавання поліномів Семейство четырехугольников
Семейство четырехугольников Умножение десятичных дробей
Умножение десятичных дробей Фигуры вращения
Фигуры вращения Число и цифра 6
Число и цифра 6 ОГЭ. Приемы решения практико-ориентированных задач
ОГЭ. Приемы решения практико-ориентированных задач