Содержание
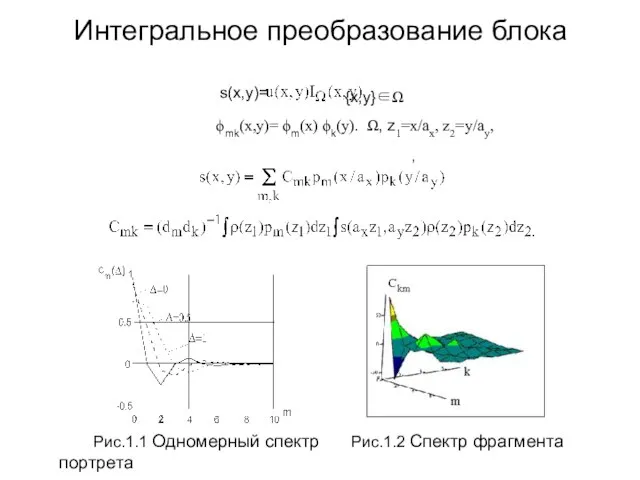
- 2. s(x,y)= {x,y}∈Ω ϕmk(x,y)= ϕm(x) ϕk(y). Ω, z1=x/ax, z2=y/ay, , Рис.1.1 Одномерный спектр Рис.1.2 Спектр фрагмента портрета
- 3. Одномерный алгоритм преобразования Чебышева. . m>0; m=0. dm=π/2, m≠0, dm=π, m=0 Tm(zn)=cos(m⋅arccos(zn))=cos(πm(n+0.5)/N), Применение квадратурных формул Гауссовского
- 4. Двумерный алгоритм преобразования (GDCT). SK(N1×N1)→S(N×N)→C(M×M)→R(L×L) . , . C(M×M). Ψ(L×M). R(L×L). , . .
- 5. Сэмплирование в GDCT формат 8/6
- 7. Скачать презентацию



 Нахождение наибольшего и наименьшего значений функции на отрезке с помощью производной
Нахождение наибольшего и наименьшего значений функции на отрезке с помощью производной Решение тригонометрических неравенств
Решение тригонометрических неравенств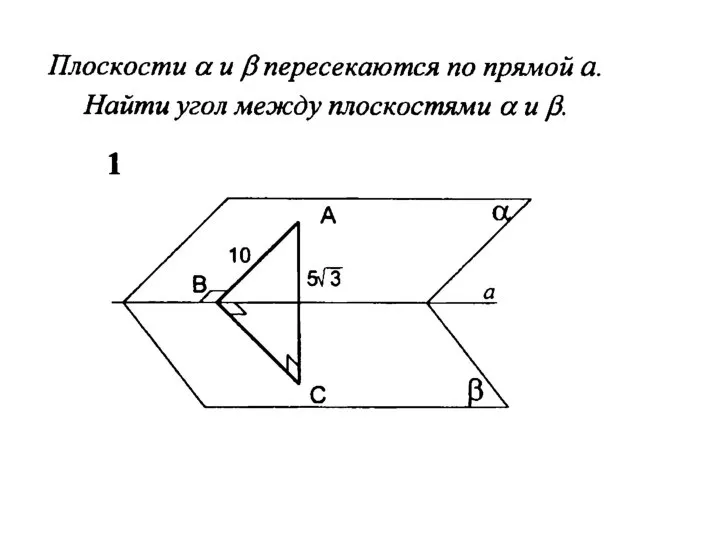 Угол между плоскостями
Угол между плоскостями Деление дробей. Взаимно-обратные числа
Деление дробей. Взаимно-обратные числа Построение треугольника по трем сторонам
Построение треугольника по трем сторонам Определители второго и третьего порядка
Определители второго и третьего порядка Сложение с переходом через десяток вида +8, +9. Считаем с гномами
Сложение с переходом через десяток вида +8, +9. Считаем с гномами Решение задач
Решение задач Задачи на проценты
Задачи на проценты Равнобедренный треугольник
Равнобедренный треугольник Задача на тему: Прогрессия
Задача на тему: Прогрессия Логарифмические уравнения
Логарифмические уравнения Золотое сечение - красота и гармония в математических расчетах
Золотое сечение - красота и гармония в математических расчетах Число и цифра 6. 1 класс
Число и цифра 6. 1 класс Измерительные работы
Измерительные работы Возмущения линейных систем и проматрицы
Возмущения линейных систем и проматрицы Этот вездесущий треугольник
Этот вездесущий треугольник Градусная мера дуги
Градусная мера дуги Иррациональные уравнения и их системы. Иррациональные неравенства
Иррациональные уравнения и их системы. Иррациональные неравенства Презентация на тему Вычисления с многозначными числами
Презентация на тему Вычисления с многозначными числами  Алгебраические выражения
Алгебраические выражения Презентация на тему Итоговый тест по математике для 1 класса
Презентация на тему Итоговый тест по математике для 1 класса  Фигуры в пространстве
Фигуры в пространстве Алгебраические структуры
Алгебраические структуры Четырехугольник . Прямоугольник. Квадрат
Четырехугольник . Прямоугольник. Квадрат Решение задач
Решение задач Презентация на тему Многообразие и происхождение культурных растений
Презентация на тему Многообразие и происхождение культурных растений  Играем и считаем
Играем и считаем