Содержание
- 2. Основной целью дисперсионного анализа является исследование значимости различия между средними. Установить различаются ли три группы или
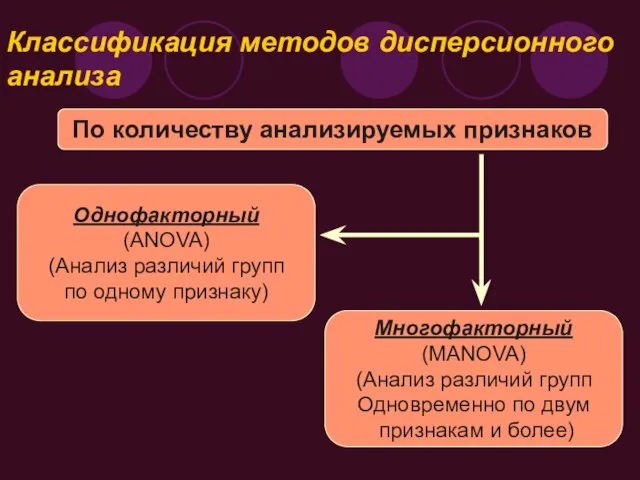
- 3. Классификация методов дисперсионного анализа По количеству анализируемых признаков Однофакторный (ANOVA) (Анализ различий групп по одному признаку)
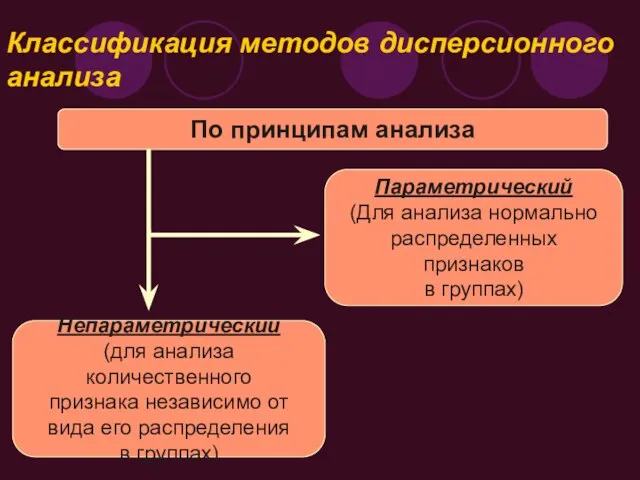
- 4. Классификация методов дисперсионного анализа По принципам анализа Параметрический (Для анализа нормально распределенных признаков в группах) Непараметрический
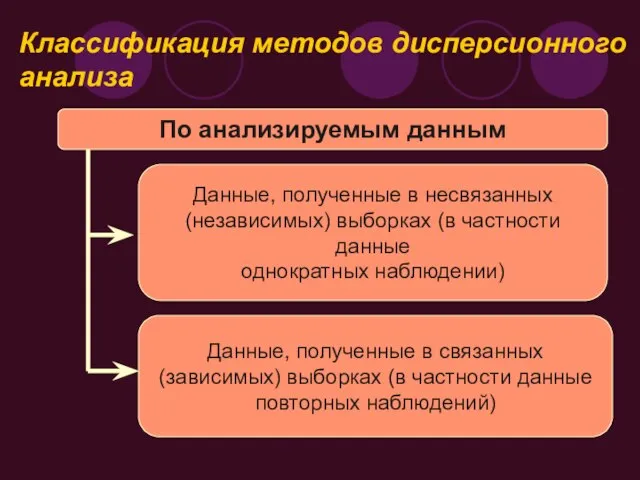
- 5. Классификация методов дисперсионного анализа По анализируемым данным Данные, полученные в несвязанных (независимых) выборках (в частности данные
- 6. Параметрический дисперсионный анализ Сравнить три или более группы по количественному нормально распределенному признаку В процедуре параметрического
- 7. Параметрический дисперсионный анализ 1. Межгрупповая вариация – вариация между средним каждой группы и общим средним значением
- 8. Параметрический дисперсионный анализ Если межгрупповая вариация оказывается статистически значимо больше внутригрупповой вариации , то можно полагать,
- 9. Параметрический дисперсионный анализ Условия применимости метода: Анализируемый признак является количественным Анализируемый признак нормально распределен в каждой
- 10. Параметрический дисперсионный анализ Этапы выполнения: Проверка гипотез о равенстве дисперсий Собственно анализ вариаций Апостериорное сравнение групп
- 11. Проверка гипотез о равенстве дисперсий ( тест Левена ) Происходит проверка нулевой гипотезы об отсутствии различий
- 12. Апостериорные сравнения групп Если при анализе вариаций получены статистически значимые результаты, то можно выяснить, которые же
- 13. Непараметрические методы исследования независимых групп (м-д Краскела-Уоллиса, медианный тест) Используется в случае необходимости сопоставить несколько групп
- 14. М-д Краскела-Уоллиса – обобщение метода Манна-Уитни для сравнения трех и более групп Медианный тест – наиболее
- 15. Непараметрические методы исследования независимых групп Условия применимости: Анализируемый признак должен быть количественным или порядковым Если распределение
- 16. Сравнение нескольких зависимых групп (непараметрический метод Фридмана) Используется с целью сопоставления признака на разных этапах динамического
- 17. Сравнение нескольких зависимых групп Условия применения метода: Анализируемые признаки должны быть количественными Вид распределения признака может
- 19. Скачать презентацию













 Решение задач
Решение задач Устный счёт. Для 5 коррекционного класса VIII вида
Устный счёт. Для 5 коррекционного класса VIII вида Основы логики
Основы логики Гамильтоновы цепи в некоторых типах линейно-выпуклых графов
Гамильтоновы цепи в некоторых типах линейно-выпуклых графов Интересные факты в тригонометрии
Интересные факты в тригонометрии Тест Смешанные числа
Тест Смешанные числа Треугольник и его виды
Треугольник и его виды Применение математики в банковском деле
Применение математики в банковском деле Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс
Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс Каков развивающий потенциал функциональной линии в курсе математики?
Каков развивающий потенциал функциональной линии в курсе математики? Решение уравнений третьей степени при подготовке к ЕГЭ
Решение уравнений третьей степени при подготовке к ЕГЭ Логарифмические функции
Логарифмические функции Многоугольники в жизни
Многоугольники в жизни Алгебра в нашей жизни
Алгебра в нашей жизни Багдадская математическая школа
Багдадская математическая школа Основы теории графов
Основы теории графов Презентация на тему Свойства степени с рациональным показателем
Презентация на тему Свойства степени с рациональным показателем  Тригонометрические функции
Тригонометрические функции Решение планиметрических задач на стереометрических чертежах
Решение планиметрических задач на стереометрических чертежах Деление с остатком
Деление с остатком Решение примеров
Решение примеров Задание В11, открытого банка ЕГЭ по математике (часть 1)
Задание В11, открытого банка ЕГЭ по математике (часть 1) Решение неравенств с одной переменной. 8 класс
Решение неравенств с одной переменной. 8 класс Параллельный перенос
Параллельный перенос Подготовка к контрольной работе
Подготовка к контрольной работе Линейные уравнения. Ярмарка по решению старинных русских задач
Линейные уравнения. Ярмарка по решению старинных русских задач Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого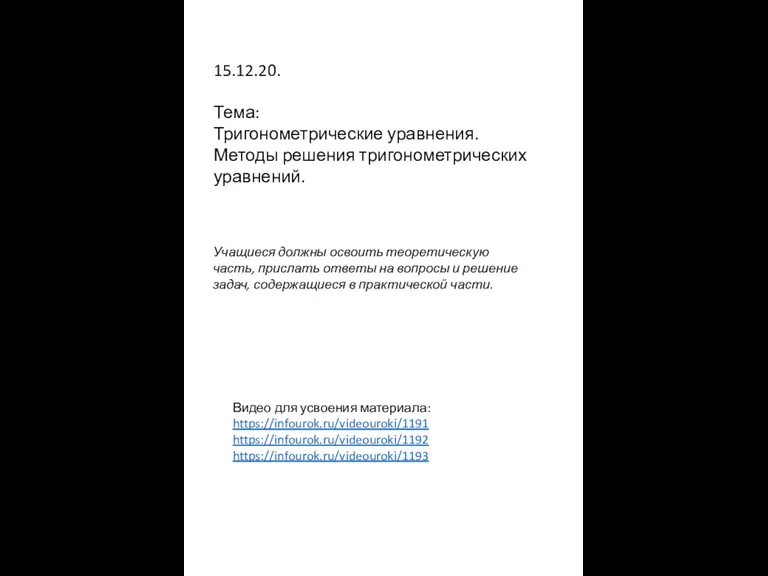 Тригонометрические уравнения. Методы решения тригонометрических уравнений
Тригонометрические уравнения. Методы решения тригонометрических уравнений