Содержание
- 2. Алгоритм построения идеально сбалансированного дерева Взять одну вершину в качестве корня. Построить тем же способом левое
- 3. Пример оформления домашней работы
- 4. РЕКУРСИВНЫЕ МЕТОДЫ ПРОХОЖДЕНИЯ ДЕРЕВЬЕВ Прямой метод прохождения определяется посещением узла в первую очередь и последующим прохождением
- 5. Варианты прохождения дерева NLR: 15, 19,21,13,11,65,70,81, 10,44,55,18 NRL: 15, 81,55, 18,10, 44, 19, 65,70, 21,11, 13
- 6. Бинарное поисковое дерево Если дерево организовано так, что для каждой вершины ti справедливо утверждение, что все
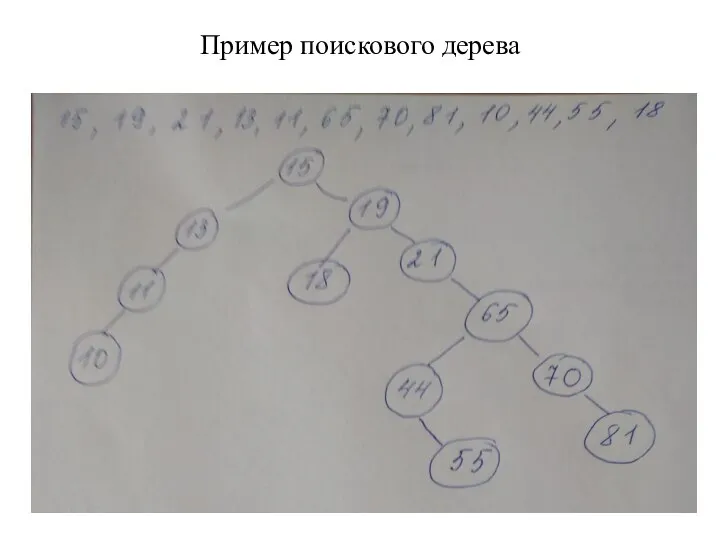
- 7. Пример построения поискового дерева 15 19 21 13 11 65 70 81 10 44 55 18
- 8. Пример поискового дерева
- 10. Скачать презентацию






 Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Презентация на тему Повторяем таблицу умножения
Презентация на тему Повторяем таблицу умножения  Дробные рациональные уравнения. Задания для интерактивной доски. 8 класс
Дробные рациональные уравнения. Задания для интерактивной доски. 8 класс Презентация на тему Проценты
Презентация на тему Проценты  Математическая викторина. 1 тур. Занимательные задачи
Математическая викторина. 1 тур. Занимательные задачи Римские цифры
Римские цифры Презентация на тему Аксиома параллельных прямых
Презентация на тему Аксиома параллельных прямых  Среднее арифметическое
Среднее арифметическое Прямоугольный параллелепипед
Прямоугольный параллелепипед Треугольник. Задачи по готовым чертежам (7 класс)
Треугольник. Задачи по готовым чертежам (7 класс) Геометрический и физический смысл производной
Геометрический и физический смысл производной Тест. Реши. И ты станешь уважать себя
Тест. Реши. И ты станешь уважать себя Эварист Галуа
Эварист Галуа ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА Равнобедренный треугольник и его свойства, 7 класс
Равнобедренный треугольник и его свойства, 7 класс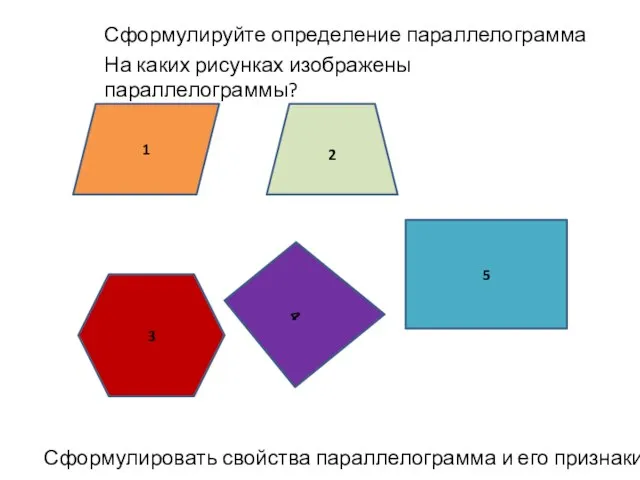 Презентация на тему Параллелограмм и трапеция (8 класс)
Презентация на тему Параллелограмм и трапеция (8 класс)  Шкалы и координаты
Шкалы и координаты Подобные треугольники
Подобные треугольники Делители и кратные
Делители и кратные Работа по введению и усвоению определений или Семь вопросов Квинтилиана
Работа по введению и усвоению определений или Семь вопросов Квинтилиана Многоугольники в окружающем нас мире
Многоугольники в окружающем нас мире Повторение. Свойства умножения. Свойства деления
Повторение. Свойства умножения. Свойства деления Комплeксные числа. Арифметические операции над ними (10 класс)
Комплeксные числа. Арифметические операции над ними (10 класс) Метод типологии
Метод типологии Схема Горнера
Схема Горнера Решение задач по геометрии
Решение задач по геометрии Четные и нечетные функции. 10 класс
Четные и нечетные функции. 10 класс Алгебра логики
Алгебра логики