Содержание
- 2. Основы теории оболочек вращения безмоментная теория оболочек; моментная теория оболочек. Оболочка является более сложным объектом –
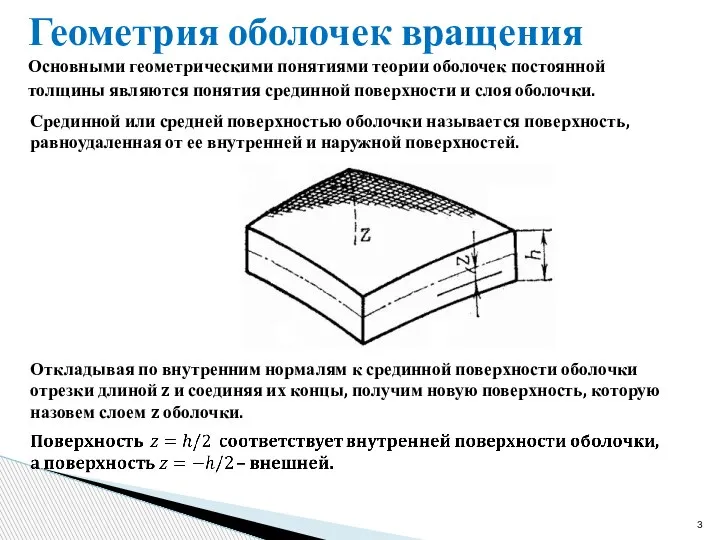
- 3. Геометрия оболочек вращения Срединной или средней поверхностью оболочки называется поверхность, равноудаленная от ее внутренней и наружной
- 4. Геометрия оболочек вращения Геометрия оболочки вращения полностью определяется формой ее срединной поверхности: сферические; конические; цилиндрические. Обычно
- 5. Геометрия оболочек вращения Срединная поверхность оболочки вращения получается в результате вращения плоской кривой относительно оси, лежащей
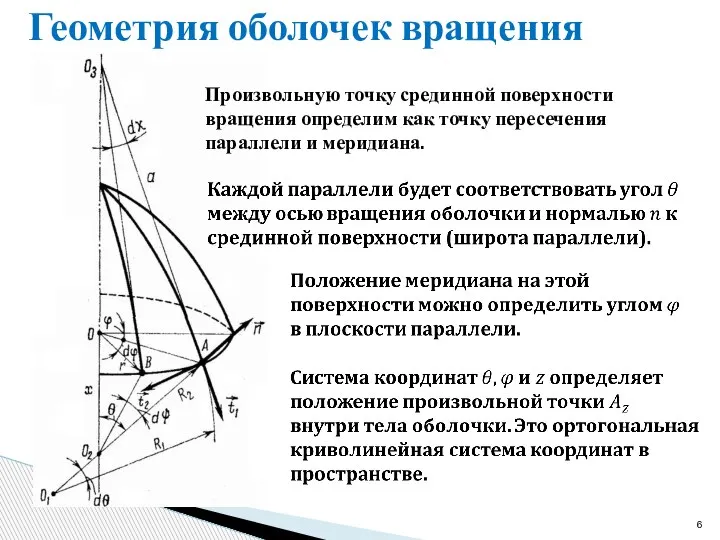
- 6. Геометрия оболочек вращения Произвольную точку срединной поверхности вращения определим как точку пересечения параллели и меридиана.
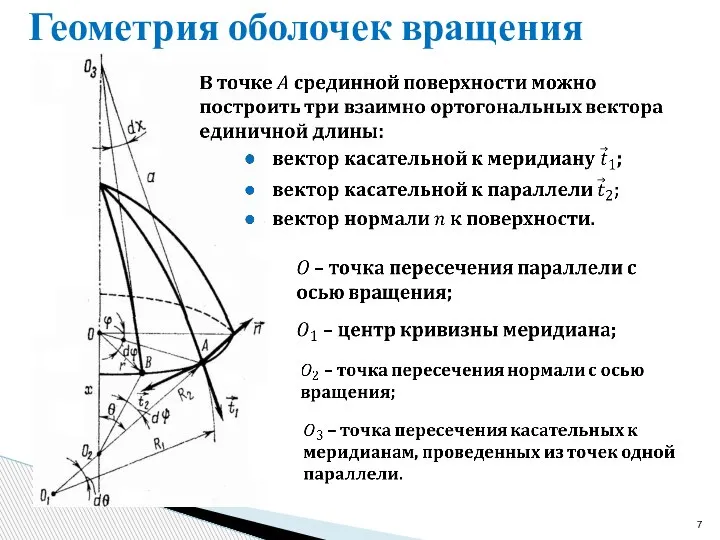
- 7. Геометрия оболочек вращения
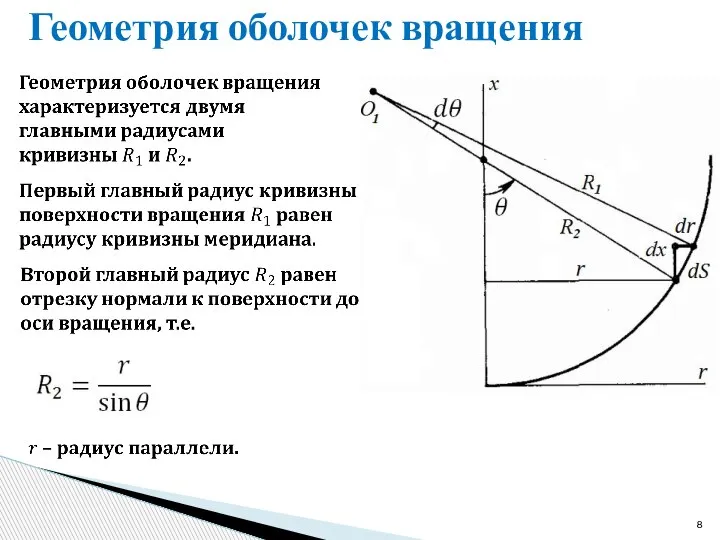
- 8. Геометрия оболочек вращения
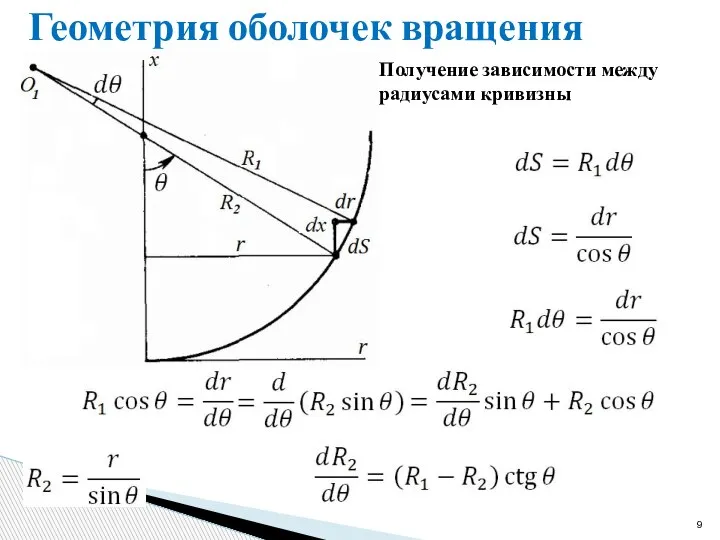
- 9. Геометрия оболочек вращения Получение зависимости между радиусами кривизны
- 10. Гипотезы Кирхгофа остается прямолинейным, нормальным к деформированной поверхности; сохраняет свою длину. 1. Кинематическая гипотеза. Нормальный к
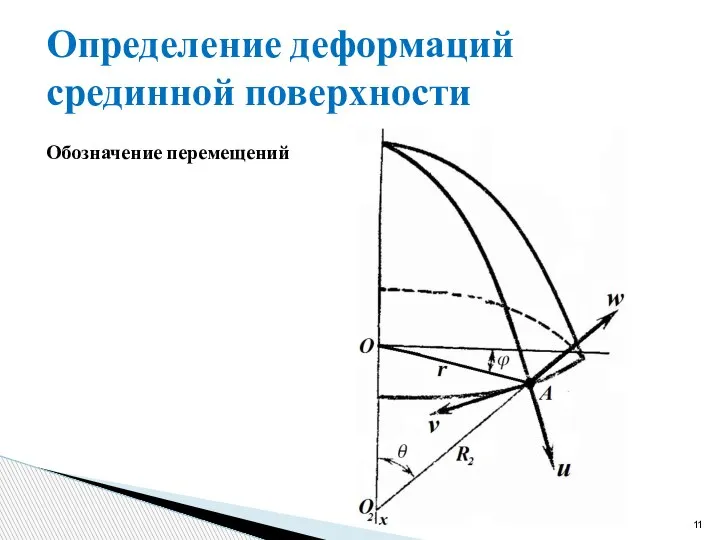
- 11. Определение деформаций срединной поверхности Обозначение перемещений
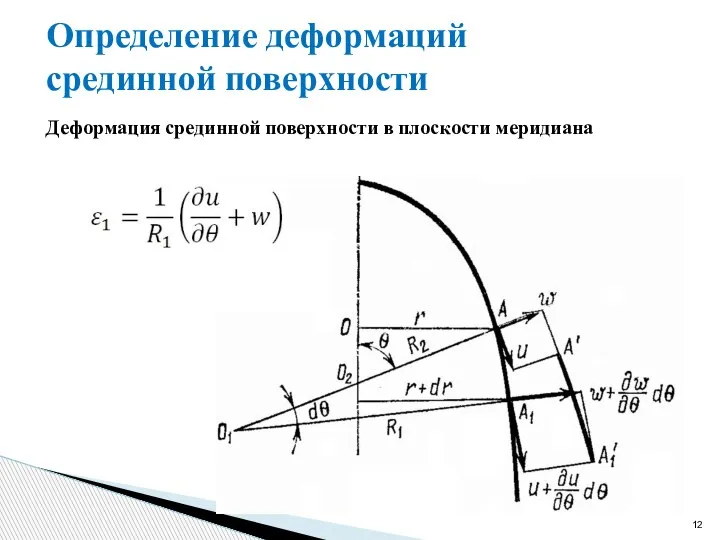
- 12. Определение деформаций срединной поверхности Деформация срединной поверхности в плоскости меридиана
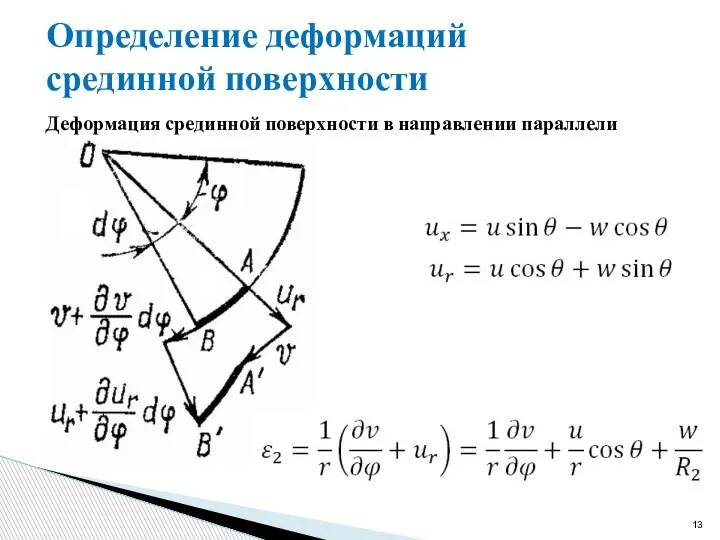
- 13. Определение деформаций срединной поверхности Деформация срединной поверхности в направлении параллели
- 14. Определение деформаций срединной поверхности Деформация сдвига элемента срединной поверхности оболочки
- 15. Определение деформаций срединной поверхности
- 16. Определение деформаций срединной поверхности Цилиндрическая оболочка
- 17. Определение деформаций срединной поверхности Сферическая оболочка
- 18. Безмоментная теория оболочек Согласно этой теории считают, что изгибающие моменты равны нулю и, следовательно, предполагают, что
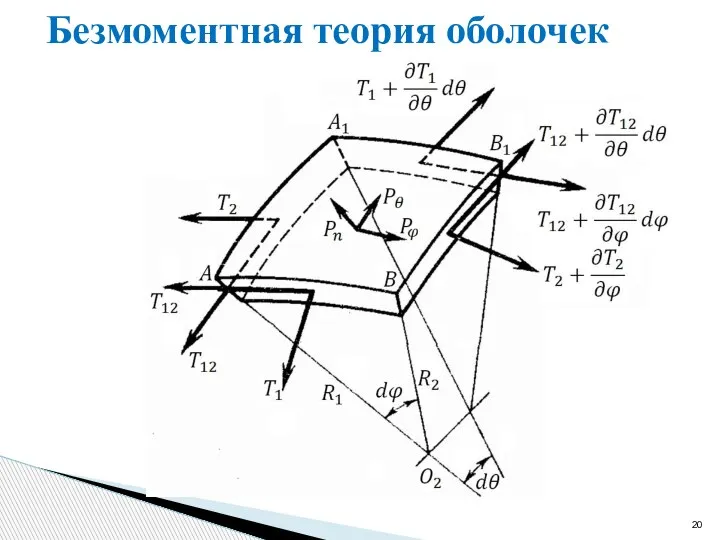
- 19. Безмоментная теория оболочек В безмоментной теории оболочек эти напряжения считаются равномерно распределенными по толщине оболочки. Погонные
- 20. Безмоментная теория оболочек
- 21. Безмоментная теория оболочек Уравнения равновесия – уравнение Лапласа
- 22. Безмоментная теория оболочек Физические соотношения Геометрические соотношения
- 23. Уравнения безмоментной теории оболочек для осесимметричной задачи Уравнения равновесия
- 24. Уравнения безмоментной теории оболочек для осесимметричной задачи Физические соотношения Геометрические соотношения
- 25. Сферическая оболочка при действии внутреннего давления Для сферической оболочки По условиям полной симметрии для сферы Из
- 26. Цилиндрическая оболочка при действии внутреннего давления Для цилиндрической оболочки Из уравнения Лапласа Кольцевое напряжение Осевое напряжение
- 27. Цилиндрическая оболочка при действии внутреннего давления Осевая деформации Перемещение Погонные усилия Окружная деформация
- 28. Цилиндрическая и сферическая оболочка при действии внутреннего давления В месте стыка цилиндра и сферы увеличение радиуса
- 29. Особенности работы оболочек
- 30. Уравнения моментной теории оболочек
- 31. Уравнения моментной теории оболочек
- 32. Уравнения моментной теории оболочек Выражения для деформаций
- 33. Уравнения моментной теории оболочек Выражения для деформаций
- 34. Уравнения моментной теории оболочек Физические соотношения (слой оболочки считают находящимся в условиях ПНС):
- 35. Уравнения моментной теории оболочек меридиональное погонное усилие кольцевое погонное усилие сдвигающее погонное усилие
- 36. Уравнения моментной теории оболочек Погонные моменты: погонный изгибающий момент в меридиональной плоскости погонный окружной изгибающий момент
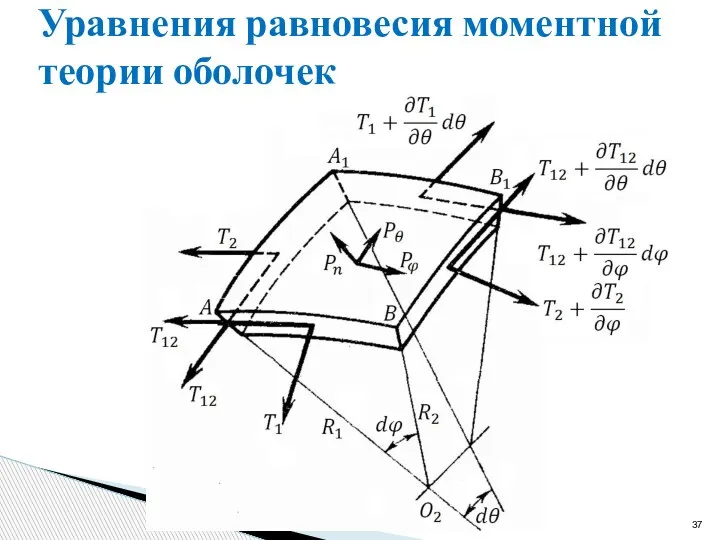
- 37. Уравнения равновесия моментной теории оболочек
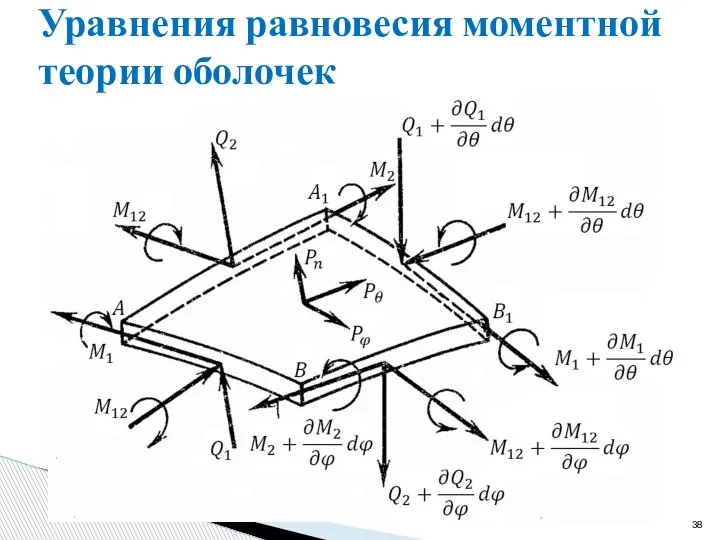
- 38. Уравнения равновесия моментной теории оболочек
- 39. Уравнения равновесия моментной теории оболочек На рисунке моменты изображены в виде векторов, перпендикулярных плоскости их действия.
- 40. Уравнения равновесия моментной теории оболочек Уравнение равновесия сил в проекции на касательную к меридиану Уравнение равновесия
- 41. Полная система уравнений моментной теории оболочек Геометрические соотношения:
- 42. Полная система уравнений моментной теории оболочек Физические соотношения:
- 43. Полная система уравнений моментной теории оболочек Уравнения равновесия:
- 44. Уравнения моментной теории оболочек при осесимметричной деформации Геометрические соотношения:
- 45. Физические соотношения Уравнения моментной теории оболочек при осесимметричной деформации
- 46. Уравнения равновесия Уравнения моментной теории оболочек при осесимметричной деформации
- 47. Краевой эффект для цилиндрической оболочки Для цилиндрической оболочки
- 48. Краевой эффект для цилиндрической оболочки Из второго уравнения равновесия сил для случая осесимметричной деформации Для усилия
- 49. Краевой эффект для цилиндрической оболочки
- 50. Краевой эффект для цилиндрической оболочки
- 52. Скачать презентацию






































 Презентация на тему ЗАДАЧИ НА ПОСТРОЕНИЕ
Презентация на тему ЗАДАЧИ НА ПОСТРОЕНИЕ  Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс Параллельные прямые
Параллельные прямые a ≥ 0 и b ≥ 0
a ≥ 0 и b ≥ 0 Признак параллельности прямых. Задачи для устной работы
Признак параллельности прямых. Задачи для устной работы На что похож наш ноль?
На что похож наш ноль? Преобразование целого выражения в многочлен
Преобразование целого выражения в многочлен Презентация на тему Единицы измерения
Презентация на тему Единицы измерения  Математический диктант. Варианты
Математический диктант. Варианты Теория вероятностей. Примеры решения задач. Задачи
Теория вероятностей. Примеры решения задач. Задачи Арифметическая прогрессия
Арифметическая прогрессия Сложение с 0. Вычитание с 0. 1 класс
Сложение с 0. Вычитание с 0. 1 класс Условная минимизация. Методы модифицированной функции Лагранжа
Условная минимизация. Методы модифицированной функции Лагранжа Вынесение общего множителя за скобки. 6 класс
Вынесение общего множителя за скобки. 6 класс Отношения и золотое сечение
Отношения и золотое сечение Абсолютные и относительные величины в статистике
Абсолютные и относительные величины в статистике Граф – набор точек, некоторые из которых соединены линиями
Граф – набор точек, некоторые из которых соединены линиями Поможем Айболиту
Поможем Айболиту Решение систем линейных уравнений при помощи компьютерных технологий
Решение систем линейных уравнений при помощи компьютерных технологий Геометрия и искусство
Геометрия и искусство Частные производные и дифференциалы высших порядков
Частные производные и дифференциалы высших порядков Новогоднее путешествие
Новогоднее путешествие Теоретические методы в морской ледотехнике
Теоретические методы в морской ледотехнике Математические основы экономической кибернетики. Элементы теории множеств и математической логики. (Лекция 1)
Математические основы экономической кибернетики. Элементы теории множеств и математической логики. (Лекция 1) Компланарные векторы
Компланарные векторы Пирамида. Применение логических законов в решении логических содержательных задач
Пирамида. Применение логических законов в решении логических содержательных задач Математическое описание случайных явлений
Математическое описание случайных явлений Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения