Параллельность прямых, прямой и плоскости

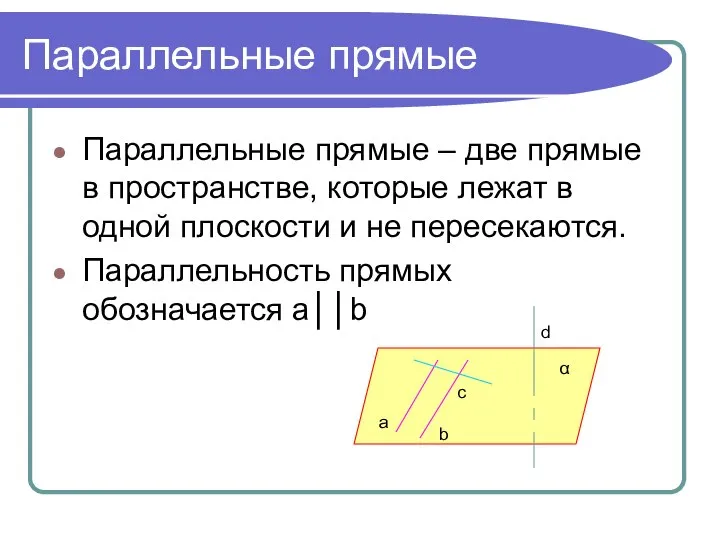
Параллельные прямые
Параллельные прямые – две прямые в пространстве, которые лежат в одной плоскости и не пересекаются.
Параллельность прямых обозначается a││b
a
b
c
d
α

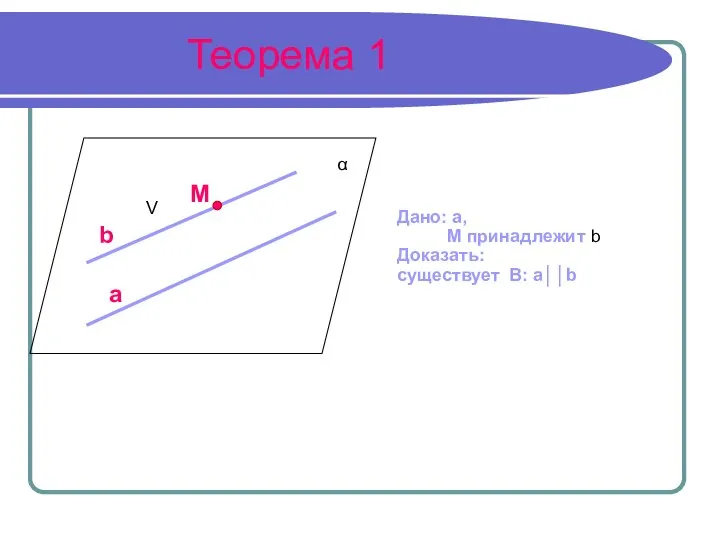
Теорема 1
Дано: a,
M принадлежит b
Доказать:
существует B: a││b
α

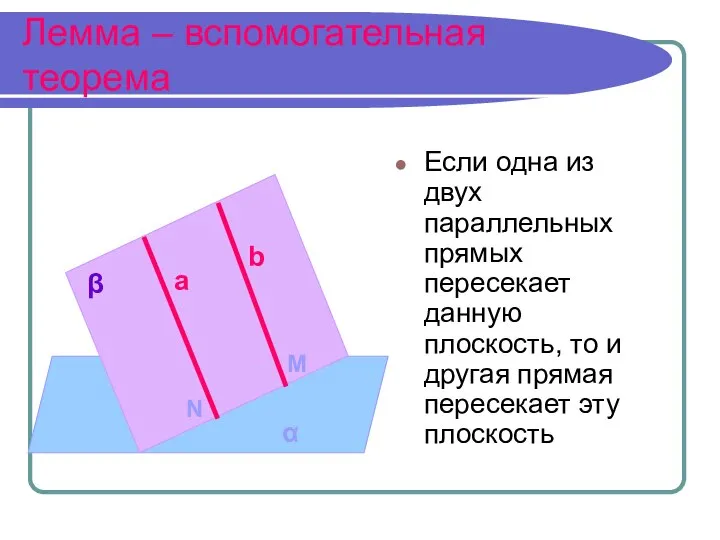
Лемма – вспомогательная теорема
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость

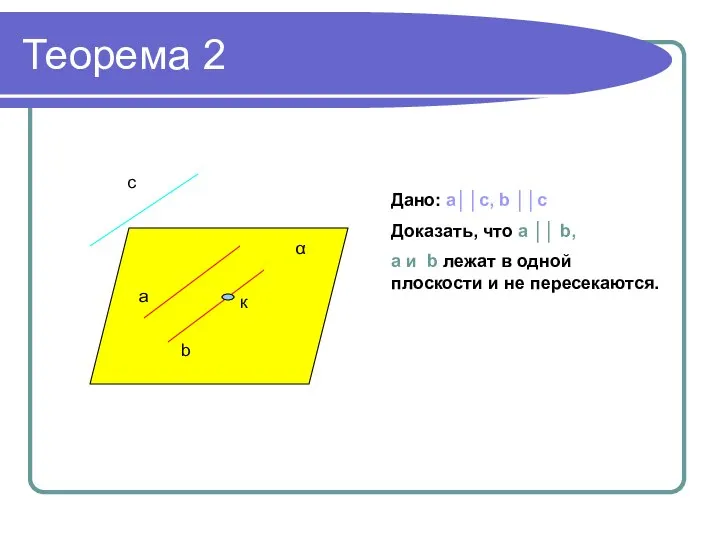
Теорема 2
α
к
a
b
c
Дано: a││с, b ││c
Доказать, что a ││ b,
a и b лежат в одной плоскости и не пересекаются.

Параллельность прямой и плоскости
Если 2 точки прямой лежат в данной плоскости, то согласно А2, вся прямая лежит в этой плоскости. Отсюда следует, что возможны 3 случая взаимного расположения прямой и плоскости в пространстве.

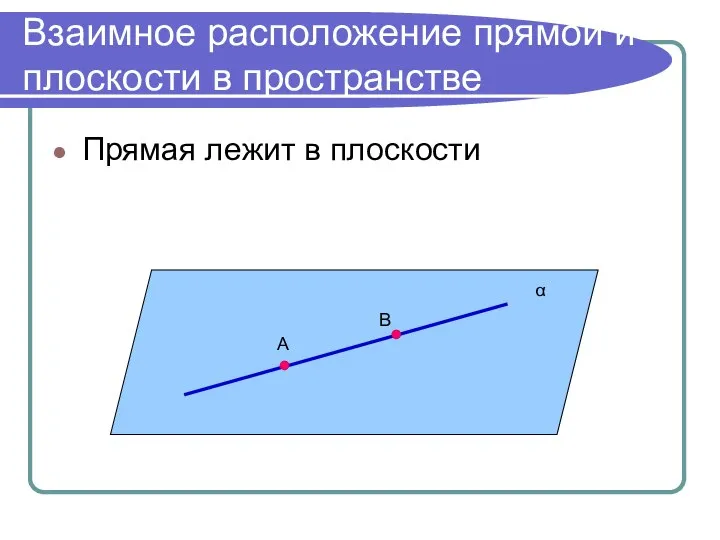
Взаимное расположение прямой и плоскости в пространстве
Прямая лежит в плоскости
α
А
В

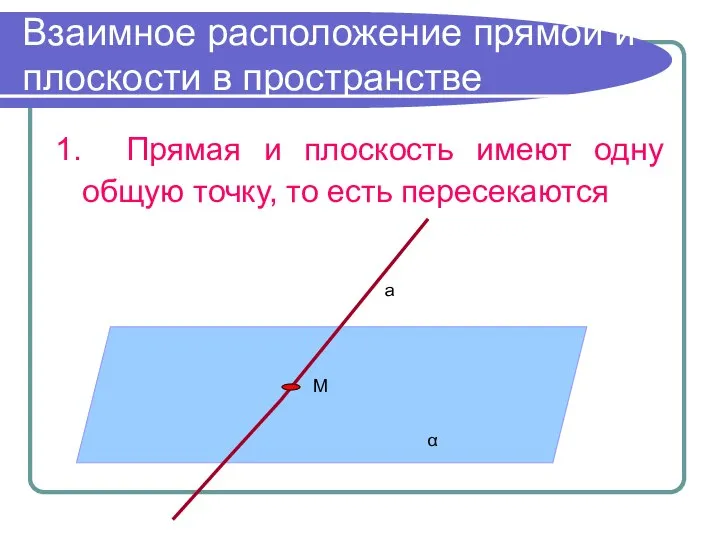
Взаимное расположение прямой и плоскости в пространстве
1. Прямая и плоскость имеют одну общую точку, то есть пересекаются
α
М
а

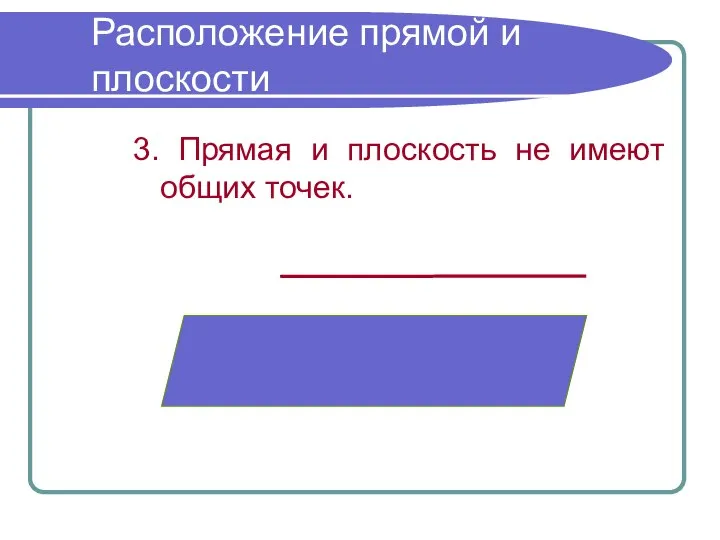
Расположение прямой и плоскости
3. Прямая и плоскость не имеют общих точек.

Определение
Прямая и плоскость называются параллельными, если они не имеют общих точек
Параллельность прямой А и плоскости обозначают так а││
α
α

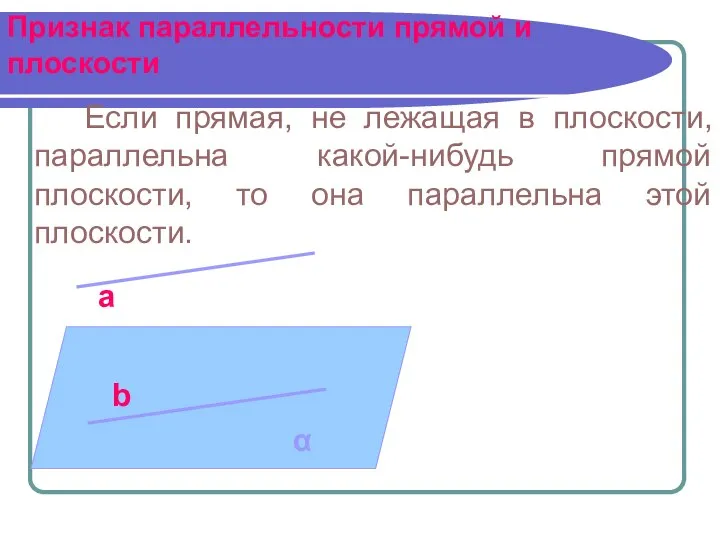
Признак параллельности прямой и плоскости
Если прямая, не лежащая в плоскости, параллельна какой-нибудь прямой плоскости, то она параллельна этой плоскости.

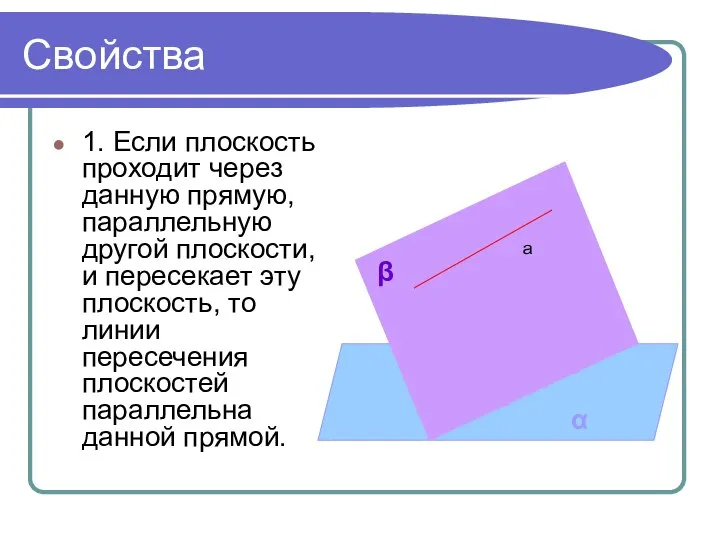
Свойства
1. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линии пересечения плоскостей параллельна данной прямой.
а