Содержание
- 2. Карл Вильгельм фон Фейербах — немецкий математик, сын криминалиста Пауля фон Фейербаха, старший брат философа Людвига
- 4. Теорема Фейербаха гласит: Окружность 9 точек(окружность Эйлера) касается вписанной и 3 вневписанных окружностей этого треугольника. Точки
- 6. Свойства и определения: Каждая точка Фейербаха лежит в точке касания пары соответствующих окружностей на линии, соединяющей
- 8. Скачать презентацию





 Положительные и отрицательные числа (6 класс)
Положительные и отрицательные числа (6 класс) Задачи на построение
Задачи на построение Задачи линейный алгоритм
Задачи линейный алгоритм Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Линии второго порядка
Линии второго порядка Отображение множеств. Диаграммы
Отображение множеств. Диаграммы Квадратный корень. Математический диктант
Квадратный корень. Математический диктант Десятичные и натуральные логарифмы
Десятичные и натуральные логарифмы Эконометрика. Временные ряды
Эконометрика. Временные ряды Решение уравнений третьей степени при подготовке к ЕГЭ
Решение уравнений третьей степени при подготовке к ЕГЭ Национальный стандарт по библиотечной статистике: преемственность и новые подходы
Национальный стандарт по библиотечной статистике: преемственность и новые подходы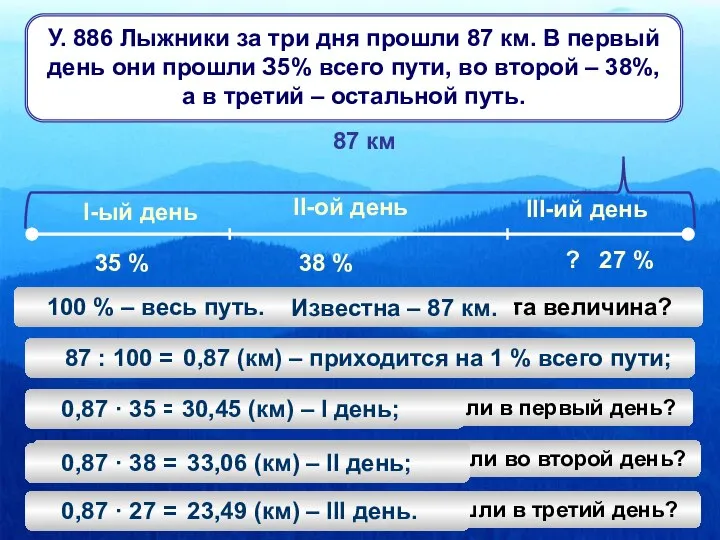 Задачи о лыжниках
Задачи о лыжниках Математический анализ
Математический анализ Четырёхугольники
Четырёхугольники Средние величины
Средние величины Проценты
Проценты Геометрия в искусстве
Геометрия в искусстве Использование метода ЛАЧХ для синтеза регуляторов манипулятора с гибким стержнем
Использование метода ЛАЧХ для синтеза регуляторов манипулятора с гибким стержнем Подобие треугольников
Подобие треугольников Возведение в квадрат суммы трех, четырех и более слагаемых
Возведение в квадрат суммы трех, четырех и более слагаемых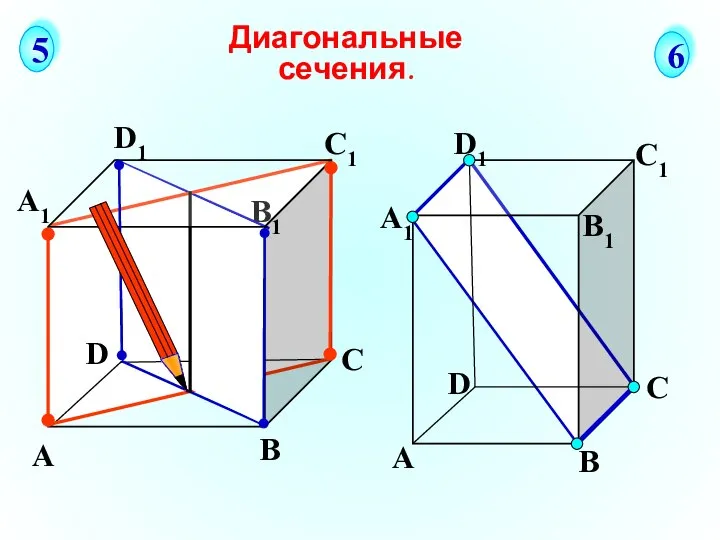 Диагональные сечения
Диагональные сечения Линейное уравнение с одной переменной
Линейное уравнение с одной переменной 38 попугаев
38 попугаев Ранг матрицы. Обратная матрица. Невырожденные матрицы
Ранг матрицы. Обратная матрица. Невырожденные матрицы Математический турнир Степень и ее свойства. 7 класс
Математический турнир Степень и ее свойства. 7 класс Презентация на тему Является ли система координат чисто математическим понятием
Презентация на тему Является ли система координат чисто математическим понятием  Статистика. Тренды
Статистика. Тренды ОГЭ 2020-21. Задание №9. Найдите корень уравнения
ОГЭ 2020-21. Задание №9. Найдите корень уравнения