Теория вероятностей, подготовка к ЕГЭ - 2019

Модуль 1. Простые задачи
В этом модуле рассматриваются задачи, для решения которых достаточно применить классическое определение вероятности.

Модуль 1. Простые задачи
Задача 1. В урне 14 красных, 9 желтых и 7 зеленых шаров. Из урны наугад достают один шар. Какова вероятность, что этот шар окажется желтым?

Задачи о выборе объектов из набора
Задача 2. В чемпионате по гимнастике участвуют 40 спортсменок: 12 из Аргентины, 9 из Бразилии, остальные — из Парагвая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Парагвая.
Задача 3. Антон, Боря , Вова и Гриша бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру будет Вова.
Задача 4. Какова вероятность того, что случайно выбранное натуральное число от 4 до 23 делится на 3?
Решение

Проверь себя
Задача 4. Научная конференция проводится в 3 дня. Всего запланировано 70 докладов — в первый день 28 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Задача 5. В сборнике билетов по химии всего 25 билетов, в 6 из них встречается вопрос по углеводородам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по углеводородам.
Задача 6. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 36 шашистов, среди которых 15 участников из России, в том числе Евгений Коротов. Найдите вероятность того, что в первом туре Евгений Коротов будет играть с каким-либо шашистом из России?
Задача 7. В среднем из 500 садовых насосов, поступивших в продажу, 4 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Задача 8. Фабрика выпускает сумки. В среднем на 80 качественных сумок приходится одна сумка со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых
Ответы

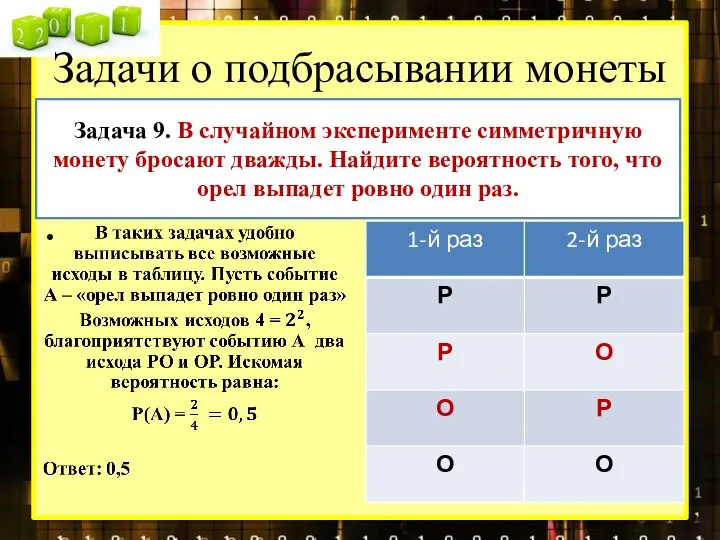
Задачи о подбрасывании монеты
Задача 9. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

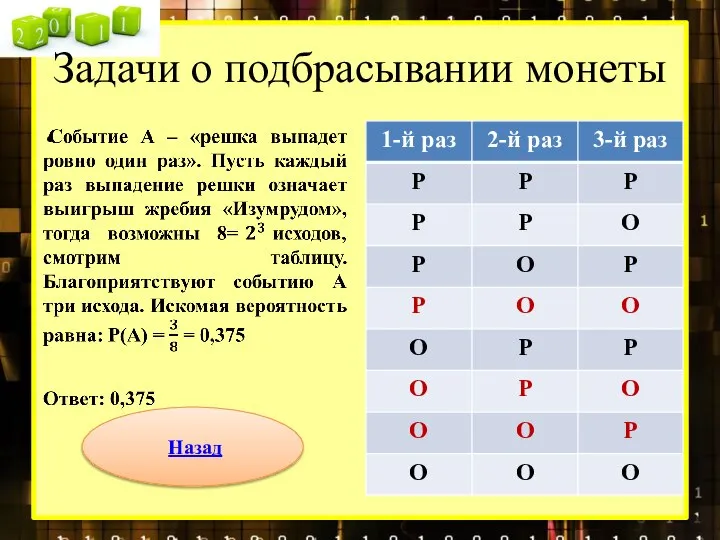
Задачи о подбрасывании монеты
Задача 10. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнет игру с мячом. Команда «Изумруд» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Изумруд» выиграет жребий ровно один раз.
Решение

Задачи о подбрасывании кубика
Задача 11. Игральный кубик бросают дважды. Найти вероятность того, что в сумме выпадет 8 очков, результат округлите до сотых.

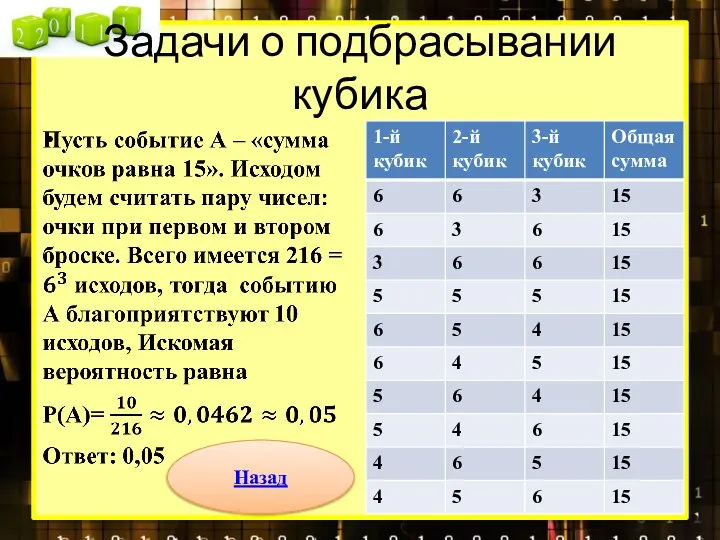
Задачи о подбрасывании кубика
Задача 12. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 15 очков. Результат округлите до сотых.
Решение

Проверь себя
Задача 13. Одновременно бросают три игральные кости. Найти вероятность того, что в сумме выпадет 5 очков, Результат округлите до сотых.
Задача 14. Определите вероятность того, что при двух бросаниях кубика выпадет разное количество очков. Результат округлить до сотых.
Задача 15. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков, Результат округлите до сотых.
Задача 16. Дважды бросают симметричную монету. Найдем вероятность того, что оба раза выпала одна сторона.
Задача 17. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
Задача 18. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу.
Ответы

Модуль2.Задачи средней трудности
При решении задач этого модуля необходимы формулы вероятности для объединения несовместных событий и пересечения независимых событий.
К этому модулю относятся задачи , связанные с частотой и процентами.
Определение. Два события А и В называются несовместными, если они не могут происходить одновременно в одном и том же испытании.
Пример. Событие А – «при бросании кубика выпало число 3 » и событие В – « выпало четное число» несовместны.
Событие С – « выпало число больше 3-х» и событие Д – «выпало четное число» являются совместными событиями.
Теорема. Вероятность суммы двух несовместных событий A и B (появление хотя бы одного события) равна сумме вероятностей этих событий:
P(A+B)=P(A) +P(B)

Модуль2.Задачи средней трудности
Определение. Два события А и В называются независимыми, если вероятность каждого из них не зависит от появления или непоявления другого (появление события А не влияет на ве­роятность события В)
Пример. Производится бросание двух костей. Событие А- «при первом подбрасывании выпало нечетное число очков» и событие В – «при втором подбрасывании выпало нечетное число очков» являются независимыми.
Пример. Пусть в урне два черных и два белых шара. Событие А – «первый извлеченный шар белый» и событие В – «второй извлеченный шар черный» являются зависимыми.
Теорема. Вероятность произведения (совместного появления) двух независимых событий равна произведению вероятностей этих событий: P(AB) = P(A) · P(B).
,
на второй кости выпало нечетное число очков ,

Задачи об объединении несовместных событий
Задача 19. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему « Ромб», равна 0,1. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,35. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение: пусть событие А означает, что школьнику достался вопрос по теме «Ромб», событие В – вопрос по теме «Тригонометрия». По условию Р(А)=0,1, Р(В)=0,35, события А и В несовместны. Искомая вероятность равна р(А+В) = 0,1+0,35 = 0,45
Ответ: 0,45

Задачи об объединении несовместных событий
Задача 20. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 25 пассажиров, равна 0,91. Вероятность того, что окажется меньше 18 пассажиров, равна 0,39. Найдите вероятность того, что число пассажиров будет от 18 до 24.
Решение
Задача 21. Вероятность того, что новая кофемолка прослужит больше года, равна 0,93. Вероятность того, что она прослужит больше двух лет, равна 0,81. Найдите вероятность того, что кофемолка прослужит меньше двух лет, но больше года.

Задачи о пересечении независимых событий
Задача 22. Если гроссмейстер А играет белыми, то он выигрывает у гроссмейстера Н. с вероятностью 0,45. Если А. играет черными, то А. выигрывает у Н. с вероятностью 0,4. Гроссмейстеры А. и Н. играют две шахматные партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Задачи о пересечении независимых событий
Задача 23. В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,4. Найдите вероятность того, что в случайный момент времени все три продавца заняты( считая, что клиенты заходят независимо друг от друга).
Задача 24. Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние три промахнулся. Результат округлите до сотых.
Решение

Назад

Проверь себя
Задача 25. В классе 21 шестиклассник, среди них два друга – Митя и Петя. Класс случайным образом делят на три группы, по 7 человек в каждой. Найдите вероятность того, что Митя и Петя окажутся в одной и той же группе.
Задача 26. Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадёт в точку G.
Задача 27. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.

Модуль 3. Трудные задачи

Задачи о зависимых событиях
Ковбой Джон попадает в муху на стене с вероятностью 0,7, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,1. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Событие А – «Ковбой Джон схватит пристрелянный пистолет и попадет из него», событие В – «Ковбой Джон схватит непристрелянный пистолет и попадет из него».
По формуле условной вероятности, Р(А)=0,4 0,9=0,36, Р(В)=0,6 0,2=0,12. Эти события несовместны, вероятность их суммы равна сумме вероятностей: 0.36+0,12=0,48. Событие, состоящее в том, что Джон промахнется, противоположное. Искомая вероятность равна: 1-0,48=0,52
Ответ: 0,52

Задачи о зависимых событиях
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Рассмотрим события
А = «кофе закончится в первом автомате»,
В = «кофе закончится во втором автомате».
Тогда A·B = «кофе закончится в обоих автоматах»,
A + B = «кофе закончится хотя бы в одном автомате».
По условию P(A) = P(B) = 0,2; P(A·B) = 0,16.
События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
P(A + B) = P(A) + P(B) − P(A·B) = 0,2 + 0,2 − 0,16 = 0,24.
Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,24 = 0,76.
Ответ: 0,76.

Задачи о зависимых событиях
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 70 этих стекол, вторая — 30. Первая фабрика выпускает 5% бракованных стекол, а вторая — 4%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Ответ: 0,204
Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов – математика, русский язык и иностранный язык. Чтобы поступить на на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов – математика, русский язык и обществознание.
Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку – 0,8, по иностранному языку – 0,7 и по обществознанию – 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решение

Решение:
Для того, чтобы поступить хоть куда-нибудь, З. нужно сдать и русский, и математику как минимум на 70 баллов, а помимо этого еще сдать иностранный язык или обществознание не менее, чем на 70 баллов. Пусть A, B, C и D – это события, в которых З. сдает соответственно математику, русский, иностранный и обществознание не менее, чем на 70 баллов. Тогда поскольку
Р(С + D) = P(C) + P(D) – P(C · D),
для вероятности поступления имеем:
P(AB(C + D)) = P(A) · P(B) · P(C + D) = P(A) · P(B) · (P(C) + P(D) – P(C) · P(D)) =
= 0,6 · 0,8 · (0,7 + 0,5 – 0,7 · 0,5) = 0,408.
Ответ: 0,408.
Назад

Проверь себя
Вариант 1
1)На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 6 прыгунов из Германии и 10 прыгунов из США. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что одиннадцатым будет выступать прыгун из Германии.
2)В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 2 очка. Результат округлите до сотых.
3)На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,35. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
4)В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
5)В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.

Проверь себя
1)На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 6 прыгунов из Германии и 10 прыгунов из США. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что одиннадцатым будет выступать прыгун из Германии.
2)В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 2 очка. Результат округлите до сотых.
3)На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,35. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
4)В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
5)В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Ответы
1.0,5
2. 0,06
3. 0,6
3. 0,6
5. 0,6

Использованная литература
Алгебра и начала математического анализа.11 класс/ Ю.М.Колягин, М.В.Ткачева, Н.Е.Федорова, М.И.Шабунин. – М.:Просвещение,
2011
ЕГЭ-2016: Математика: самое полное издание типовых вариантов заданий/ авт.-сост. И.В.Ященко, И.Р. Высоцкий; под ред. А.Л.Семёнова, И.В.Ященко.- Москва: АСТ: Астрель, 2014.
http://alexlarin.net/ege/2014/b102014.html
http://math.reshuege.ru/test?a=catlistwstat

Назад

Задачи о подбрасывании монеты
Назад

Задачи о подбрасывании кубика
Назад

Задачи об объединении несовместных событий
Назад

Проверь себя
Задача 4. 0,3
Задача 5. 0,24
Задача 6. 0,4
Задача 7. 0,992
Задача 8. 0 99
Назад