Содержание
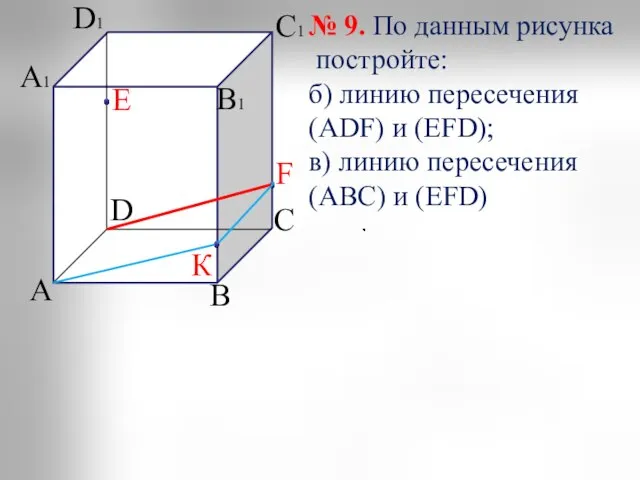
- 2. А D С В А1 В1 С1 D1 Е К F № 9. По данным рисунка
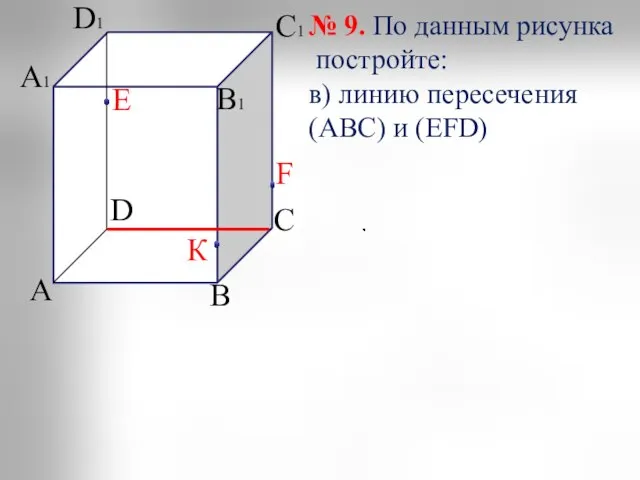
- 3. А D С В А1 В1 С1 D1 Е К F № 9. По данным рисунка
- 4. № 10. Стороны АВ и АС треугольника АВС лежат в одной плоскости. Докажите, что и медиана
- 5. 23.09.20 г. 1. Параллельные прямые в пространстве.
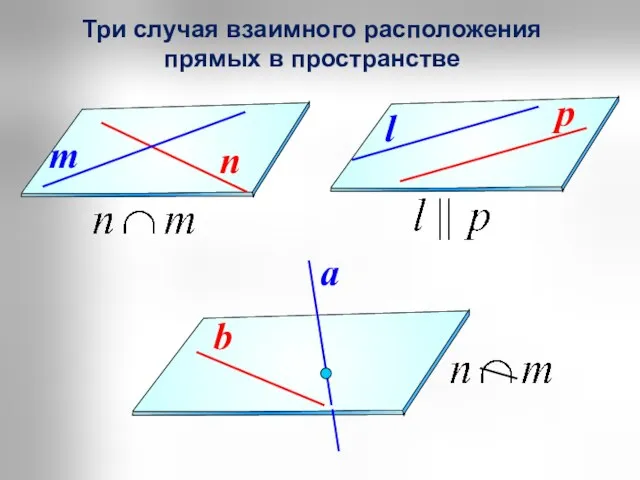
- 6. Три случая взаимного расположения прямых в пространстве
- 7. Планиметрия Стереометрия Две прямые на плоскости называются параллельными, если они не пересекаются Две прямые в пространстве
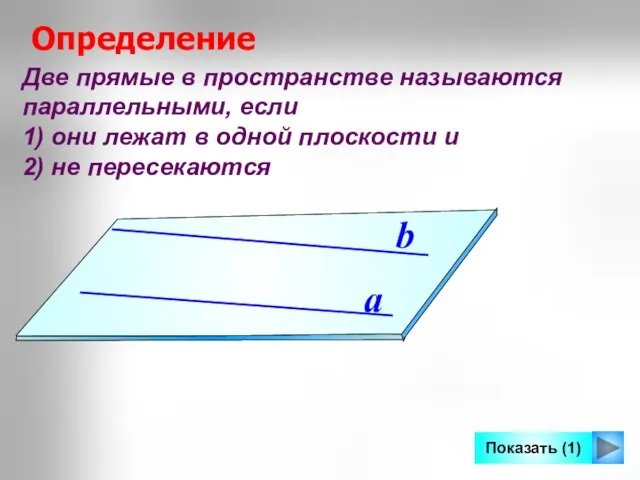
- 8. Две прямые в пространстве называются параллельными, если 1) они лежат в одной плоскости и 2) не
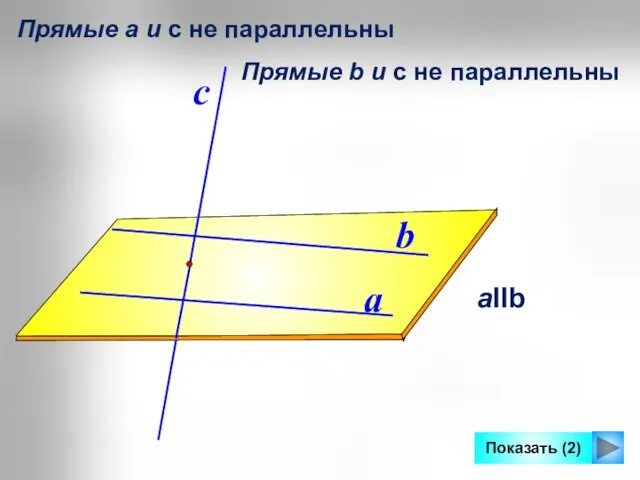
- 9. a b aIIb с Прямые а и с не параллельны Показать (2) Прямые b и с
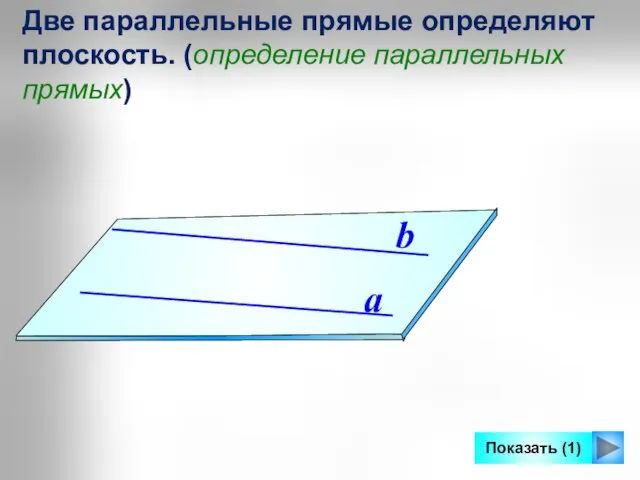
- 10. Две параллельные прямые определяют плоскость. (определение параллельных прямых) a b Показать (1)
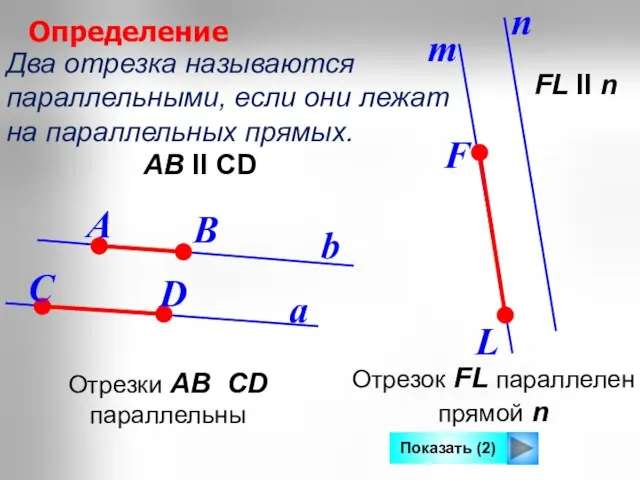
- 11. Два отрезка называются параллельными, если они лежат на параллельных прямых. a b Определение АВ II СD
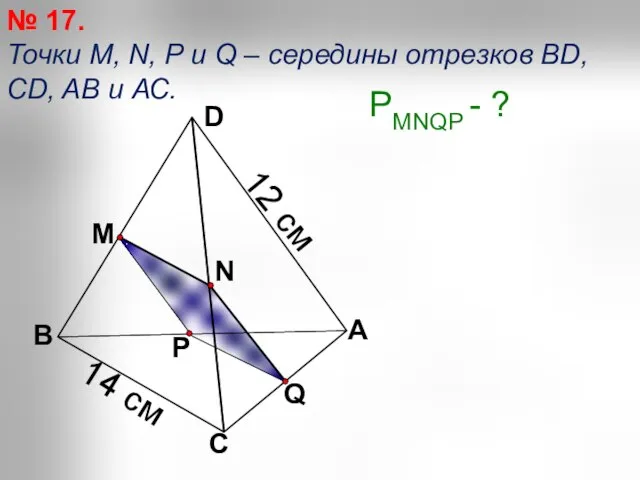
- 12. Q А С В D N M P № 17. Точки М, N, P и Q
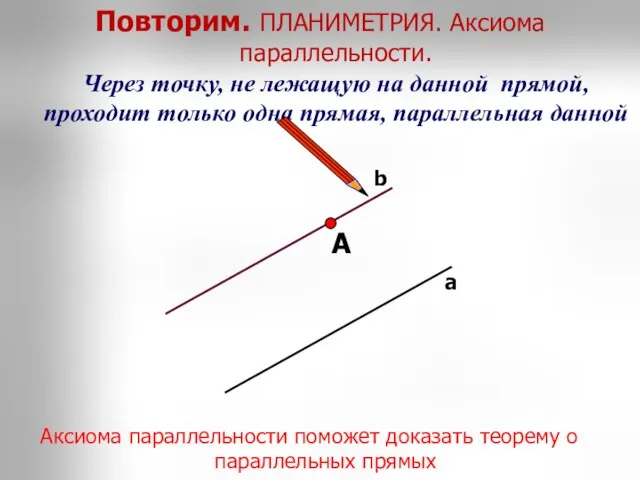
- 13. А Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной Повторим. ПЛАНИМЕТРИЯ.
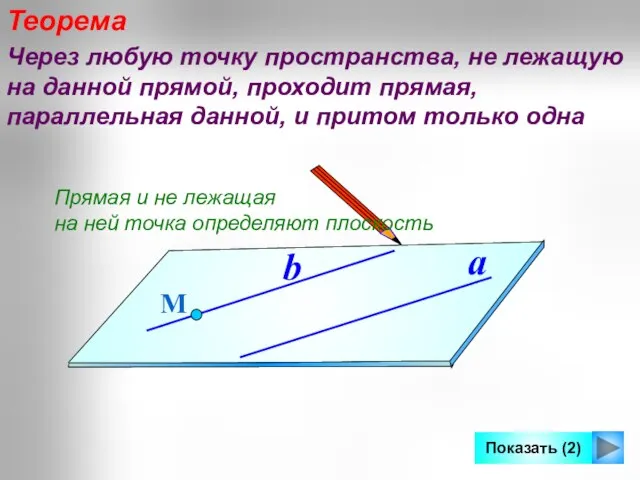
- 14. Теорема Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом
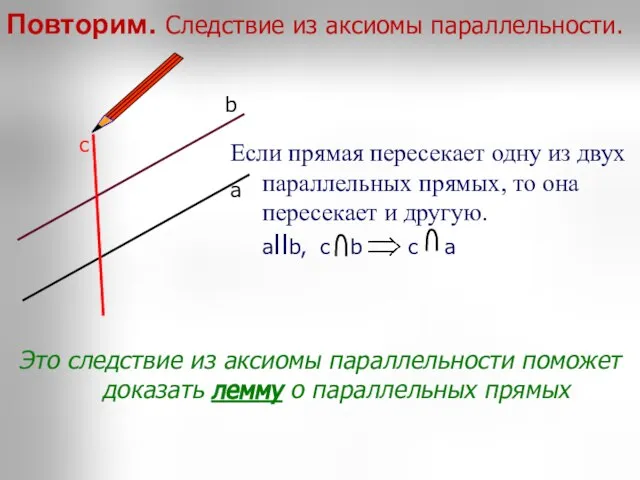
- 15. Повторим. Следствие из аксиомы параллельности. а c b Это следствие из аксиомы параллельности поможет доказать лемму
- 16. Лемма — доказанное утверждение, полезное не само по себе, а для доказательства других утверждений Греческое слово
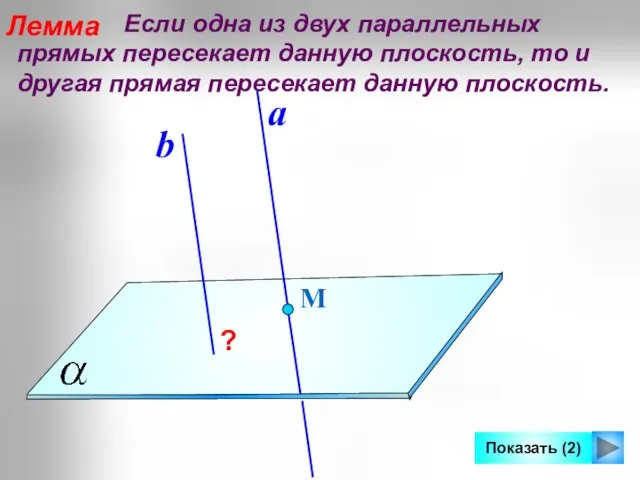
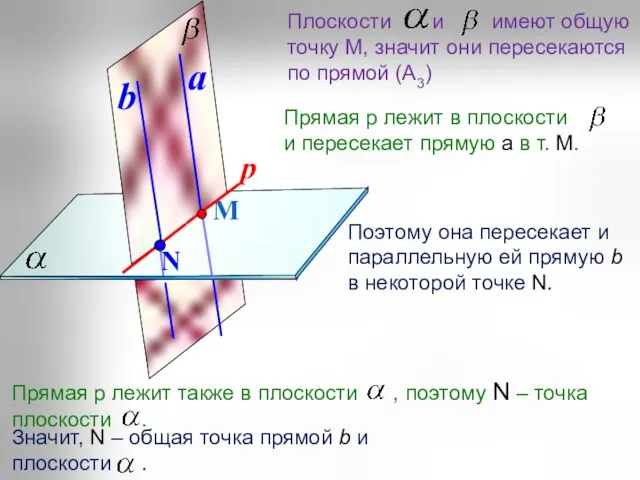
- 17. Лемма Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает данную
- 18. М a Поэтому она пересекает и параллельную ей прямую b в некоторой точке N.
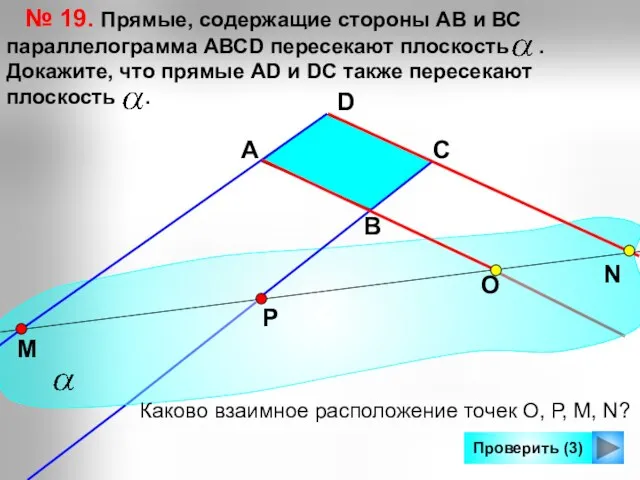
- 19. Проверить (3) № 19. Прямые, содержащие стороны АВ и ВС параллелограмма AВСD пересекают плоскость . Докажите,
- 20. 2. Параллельность трёх прямые в пространстве.
- 21. Повторим. Следствие из аксиомы параллельности. Если a//с, b//с, то … Аналогичное утверждение имеет место и для
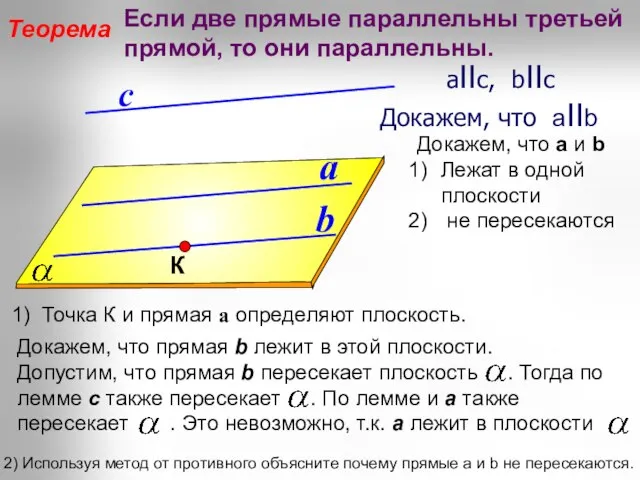
- 22. a b с Теорема Если две прямые параллельны третьей прямой, то они параллельны. aIIс, bIIс Докажем,
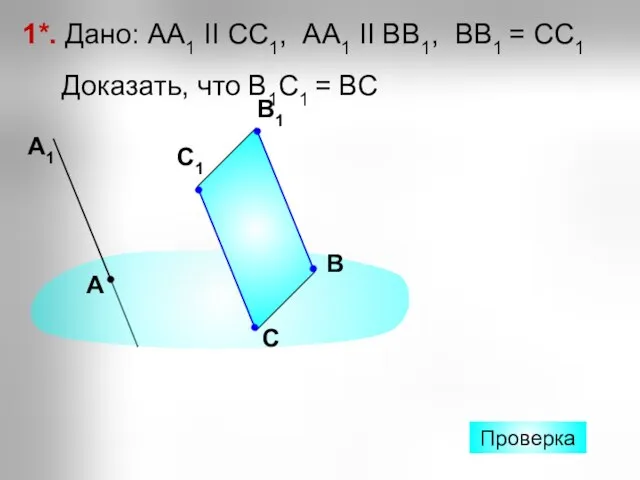
- 23. 1*. Дано: АА1 II СС1, АА1 II ВВ1, ВВ1 = СС1 Доказать, что В1С1 = ВС
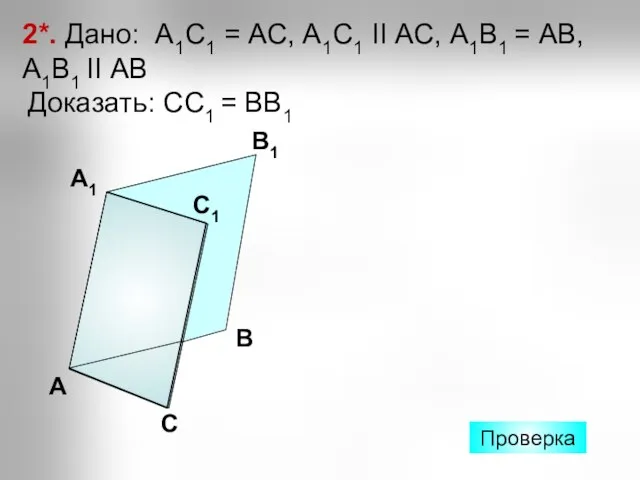
- 24. 2*. Дано: А1С1 = АС, А1С1 II АС, А1В1 = АВ, А1В1 II АВ Доказать: CС1
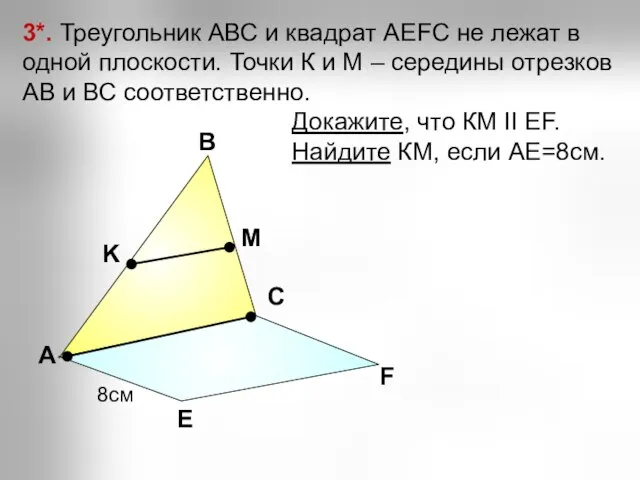
- 25. А В С Е F K M 3*. Треугольник АВС и квадрат АEFC не лежат в
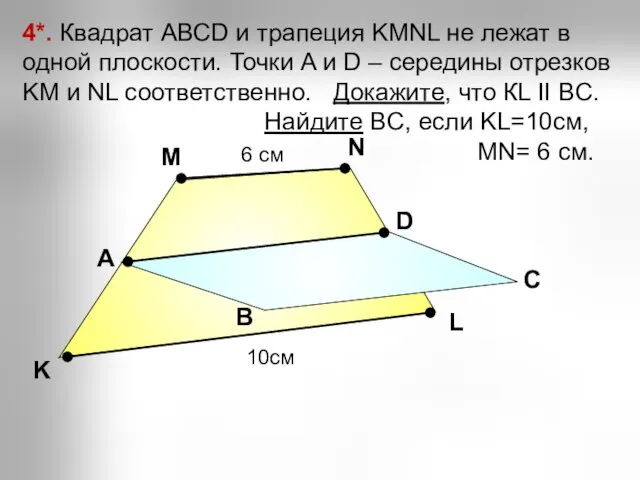
- 26. А В С С D K M 4*. Квадрат АВСD и трапеция KMNL не лежат в
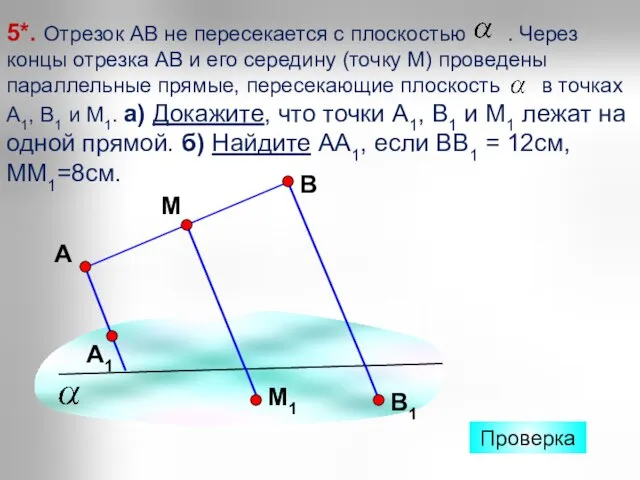
- 27. 5*. Отрезок АВ не пересекается с плоскостью . Через концы отрезка АВ и его середину (точку
- 29. Скачать презентацию






 Умножение и деление смешанных дробей
Умножение и деление смешанных дробей Презентация на тему Готфрид Вильгельм Лейбниц
Презентация на тему Готфрид Вильгельм Лейбниц  Консультація до іспиту ТМДМ
Консультація до іспиту ТМДМ Презентация на тему Геометрические тела. Многогранники
Презентация на тему Геометрические тела. Многогранники  Признаки равенства треугольников
Признаки равенства треугольников Математический марафон
Математический марафон Функция. График функции
Функция. График функции Задачи на разрезание
Задачи на разрезание Иррациональные неравенства
Иррациональные неравенства Четырёхугольники. Задачи на готовых чертежах
Четырёхугольники. Задачи на готовых чертежах Решение систем уравнений способом подстановки
Решение систем уравнений способом подстановки ГИА - 2016. Задачи №9,10,11,12
ГИА - 2016. Задачи №9,10,11,12 Параллелограмм
Параллелограмм Уравнение плоскости
Уравнение плоскости Решение тригонометрических уравнений sin а
Решение тригонометрических уравнений sin а Имитационное моделирование
Имитационное моделирование Вычитание смешанных чисел. 5 класс
Вычитание смешанных чисел. 5 класс Метод рекуррентных соотношений
Метод рекуррентных соотношений Задача по математике (1 класс, задание 15)
Задача по математике (1 класс, задание 15) ЛЕКЦИЯ_6
ЛЕКЦИЯ_6 Свойства корня степени n
Свойства корня степени n Владимир Модестович Брадис и его замечательные таблицы
Владимир Модестович Брадис и его замечательные таблицы Арксинус. Решение уравнения Sin t = a
Арксинус. Решение уравнения Sin t = a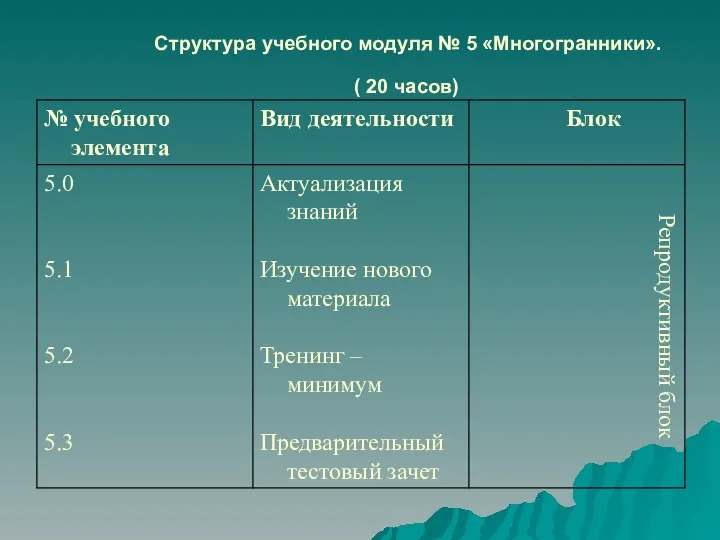 Структура учебного модуля № 5 Многогранники. ( 20 часов)
Структура учебного модуля № 5 Многогранники. ( 20 часов) Презентация на тему Звездчатые многогранники
Презентация на тему Звездчатые многогранники  Функции у=|x| и ей график
Функции у=|x| и ей график Стационарный режим теплообмена с фазовым переходом
Стационарный режим теплообмена с фазовым переходом Прямоугольник
Прямоугольник