Содержание
- 2. Планиметрия Стереометрия Две прямые на плоскости называются параллельными, если они не пересекаются. Две прямые в пространстве
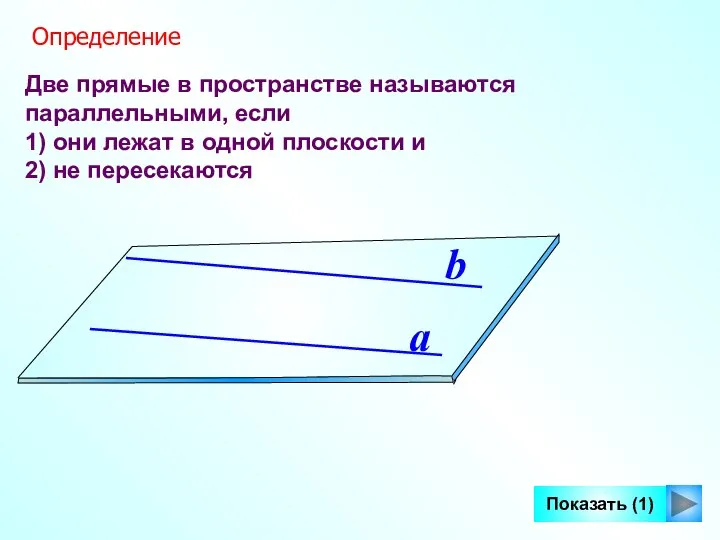
- 3. Две прямые в пространстве называются параллельными, если 1) они лежат в одной плоскости и 2) не
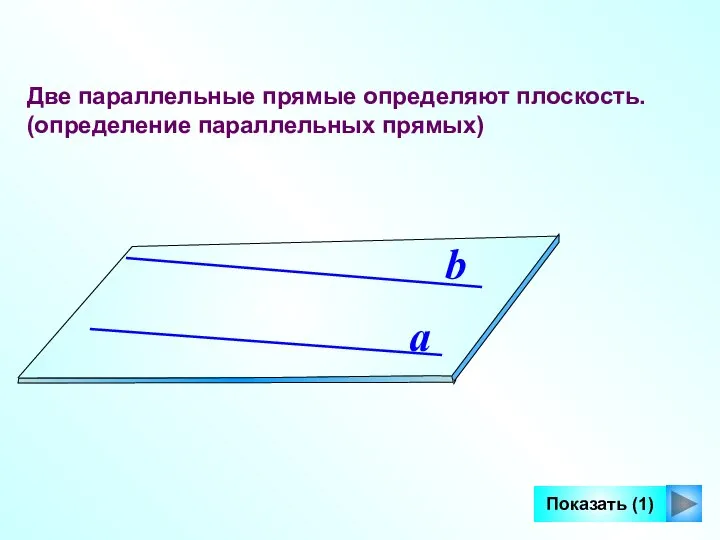
- 4. Две параллельные прямые определяют плоскость. (определение параллельных прямых) a b Показать (1)
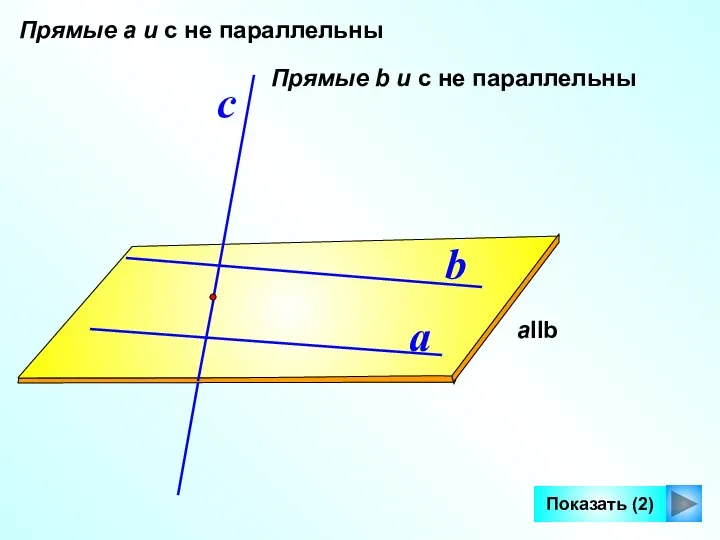
- 5. a b aIIb с Прямые а и с не параллельны Показать (2) Прямые b и с
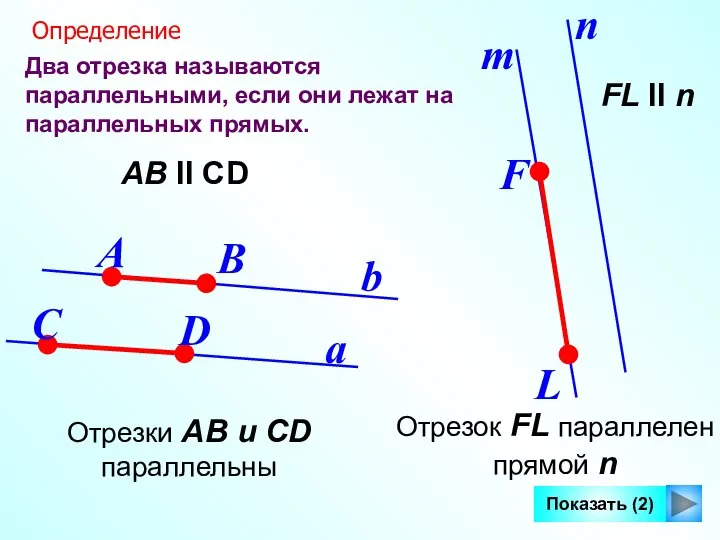
- 6. Два отрезка называются параллельными, если они лежат на параллельных прямых. a b Определение АВ II СD
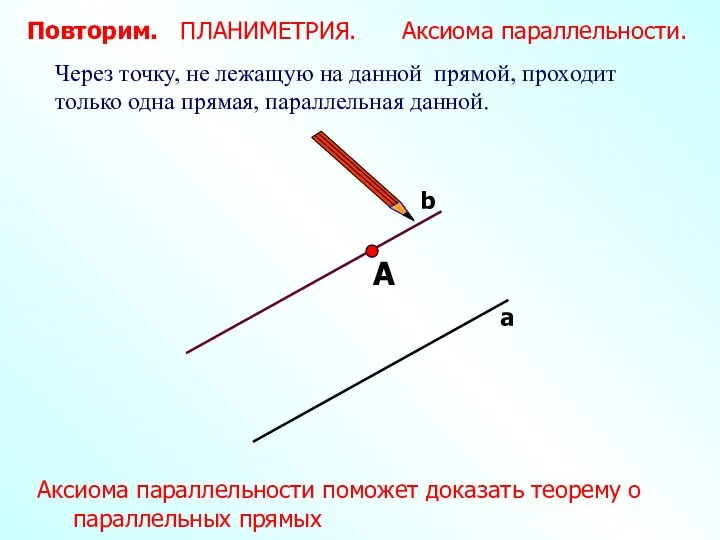
- 7. А Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Повторим. ПЛАНИМЕТРИЯ.
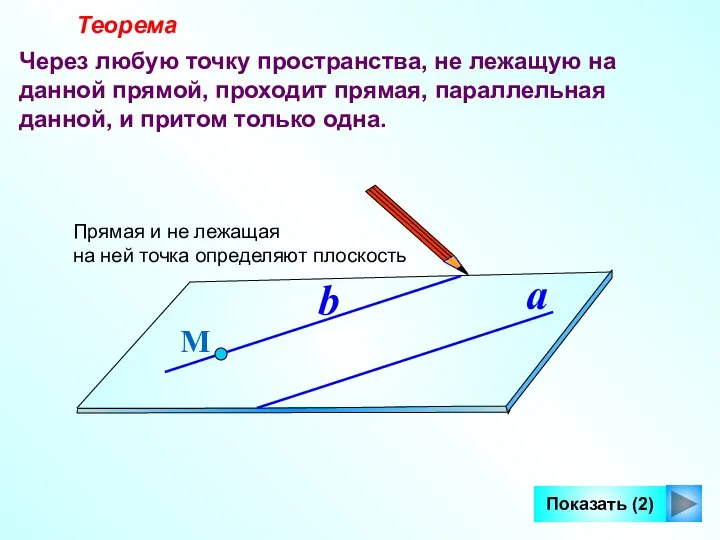
- 8. Теорема Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом
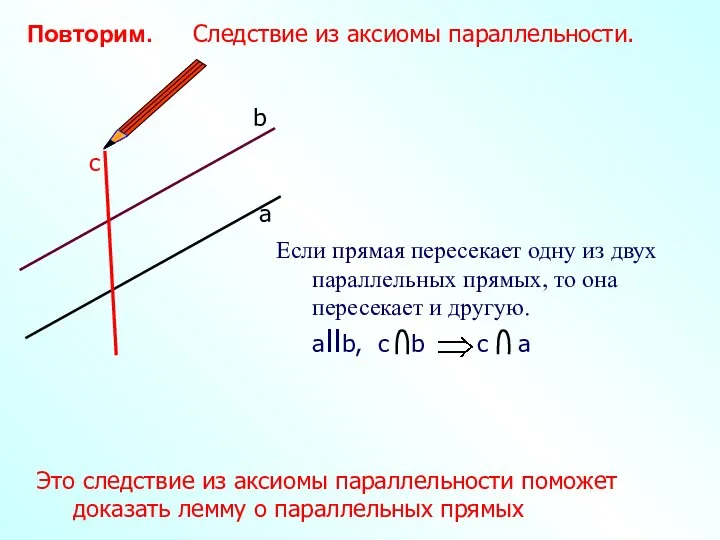
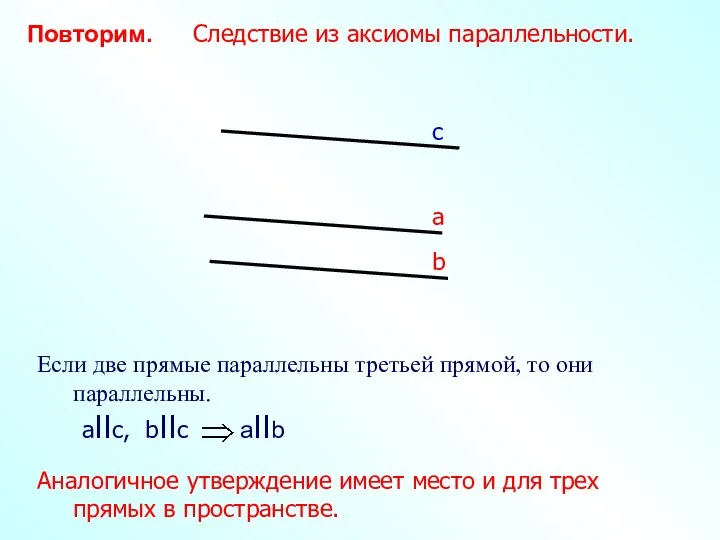
- 9. Повторим. Следствие из аксиомы параллельности. а c b Это следствие из аксиомы параллельности поможет доказать лемму
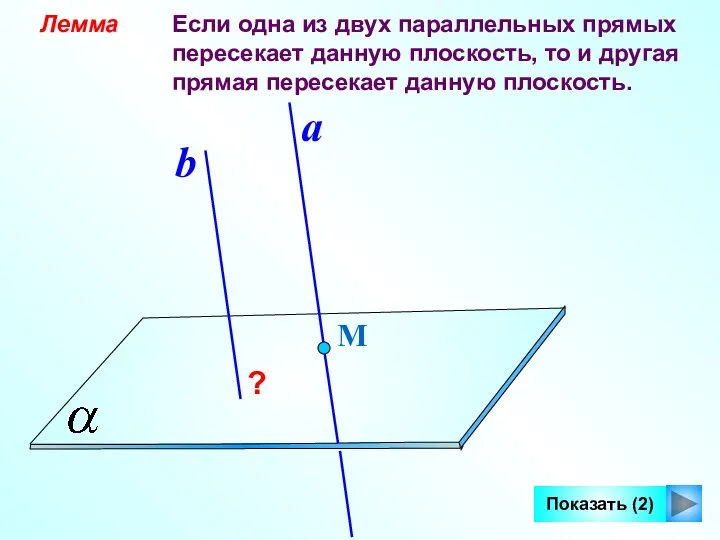
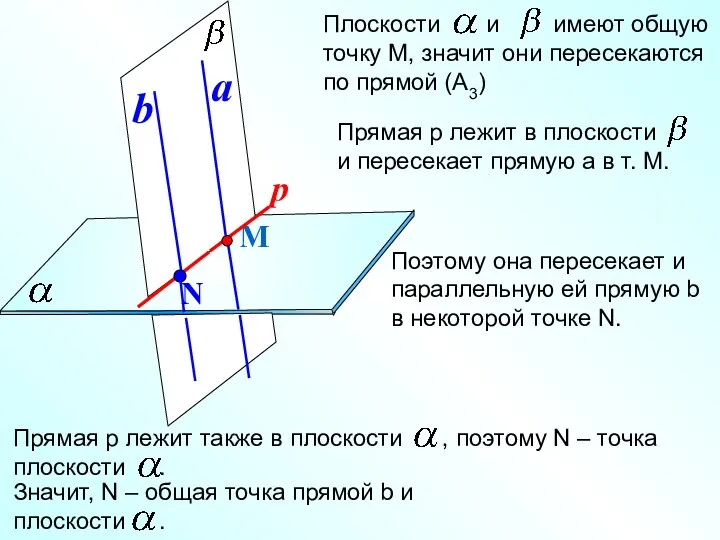
- 10. Лемма Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает данную
- 11. М a Поэтому она пересекает и параллельную ей прямую b в некоторой точке N.
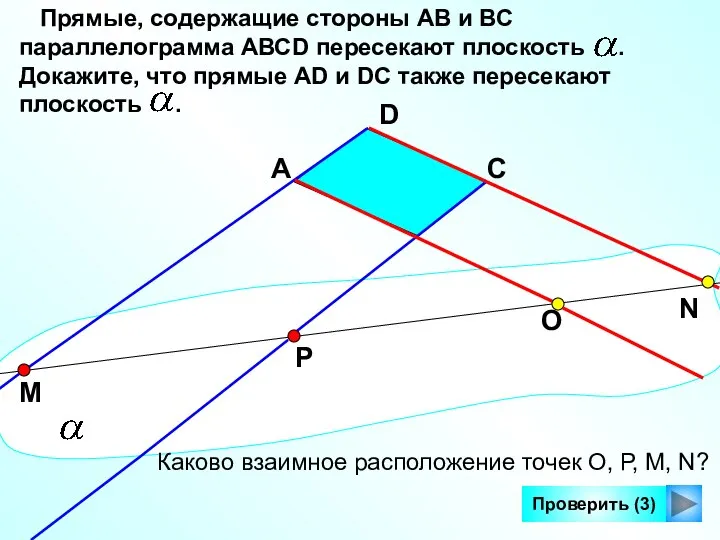
- 12. Проверить (3) Прямые, содержащие стороны АВ и ВС параллелограмма AВСD пересекают плоскость . Докажите, что прямые
- 13. Повторим. Следствие из аксиомы параллельности. Аналогичное утверждение имеет место и для трех прямых в пространстве.
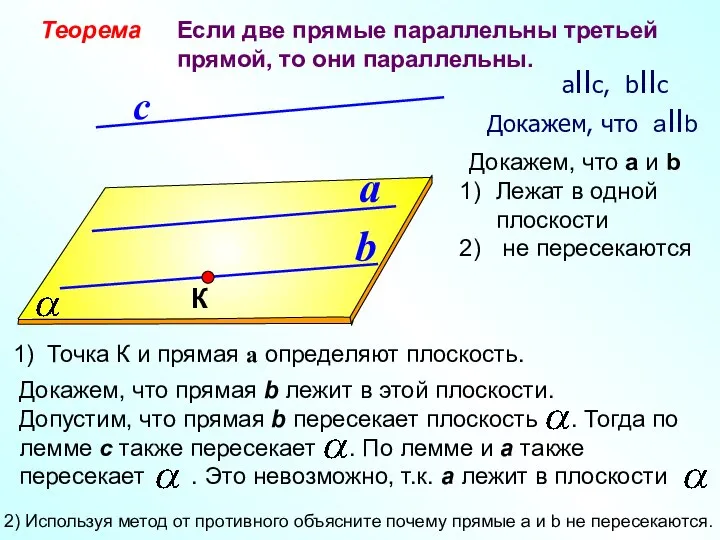
- 14. a b с Теорема Если две прямые параллельны третьей прямой, то они параллельны. aIIс, bIIс Докажем,
- 16. Скачать презентацию

 Решение задач по теме: Двумерный массив. Профильный уровень
Решение задач по теме: Двумерный массив. Профильный уровень Операции над множествами
Операции над множествами Площадь трапеции
Площадь трапеции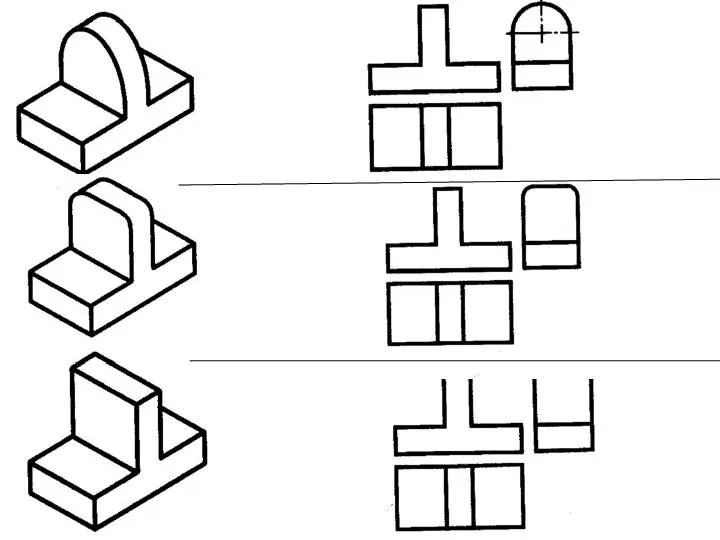 Проецирование на три взаимно перпендикулярные плоскости проекций
Проецирование на три взаимно перпендикулярные плоскости проекций Математика
Математика Вычислительная сложность алгоритма
Вычислительная сложность алгоритма Доли. 3 класс
Доли. 3 класс Задачі на проценти
Задачі на проценти 08.09
08.09 Разряды и классы чисел
Разряды и классы чисел тригонометрические неравенства (1)
тригонометрические неравенства (1)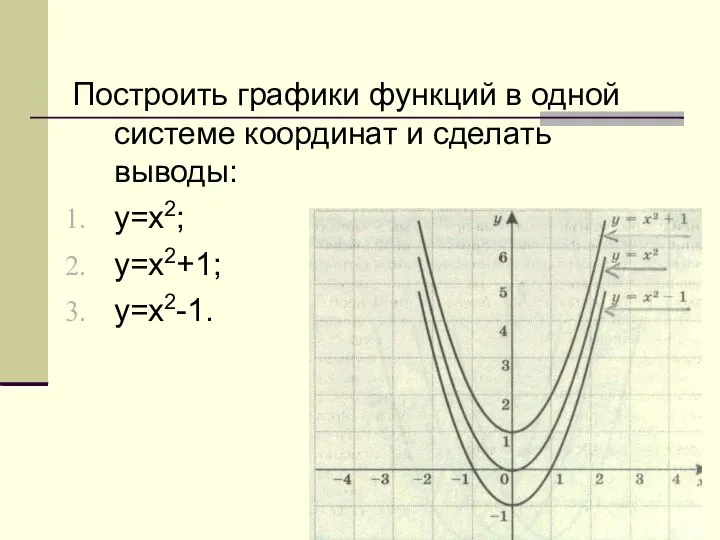 Графики функций в одной системе координат
Графики функций в одной системе координат Применение метода интервалов для решения неравенств. 8 класс
Применение метода интервалов для решения неравенств. 8 класс ЕГЭ. Математика. Задание № 5. Решение простейших тригонометрических уравнений
ЕГЭ. Математика. Задание № 5. Решение простейших тригонометрических уравнений Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1)
Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1) Ukazania_k_vypolneniyu_raboty_5
Ukazania_k_vypolneniyu_raboty_5 Сложение и вычитание смешанных чисел. Подготовка к контрольной работе
Сложение и вычитание смешанных чисел. Подготовка к контрольной работе Площадь треугольника
Площадь треугольника Начала теории вероятности
Начала теории вероятности Положительные и отрицательные числа (6 класс)
Положительные и отрицательные числа (6 класс)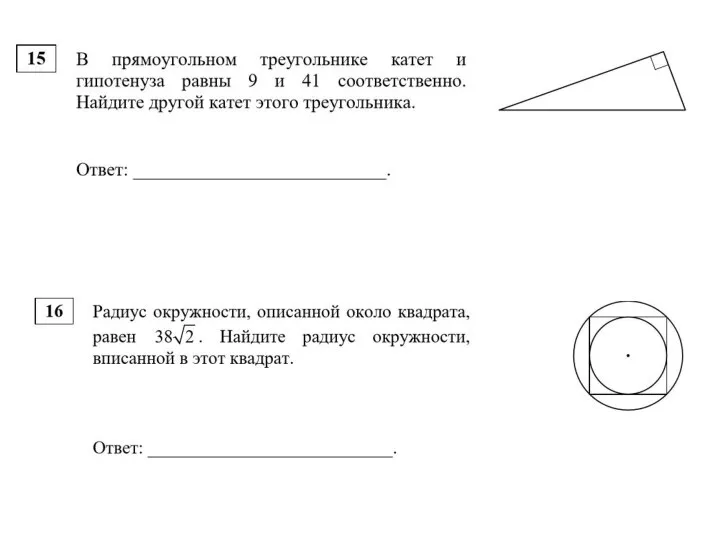 Решение задач
Решение задач Презентация на тему Многообразие и происхождение культурных растений
Презентация на тему Многообразие и происхождение культурных растений  Презентация на тему Угол. Прямой и развернутый угол
Презентация на тему Угол. Прямой и развернутый угол  Виды углов.Измерение углов
Виды углов.Измерение углов Линейное уравнение с одной переменной (7 класс)
Линейное уравнение с одной переменной (7 класс) Построение графика квадратичной функции у=ах2+bx+c, a не равно 0
Построение графика квадратичной функции у=ах2+bx+c, a не равно 0 Решение задач
Решение задач Наименьшее значение выражения
Наименьшее значение выражения