Содержание
- 2. Цели урока: обучающие: создать условия для формирования основных понятий перпендикуляра, наклонной, проекции наклонной, расстояния от точки
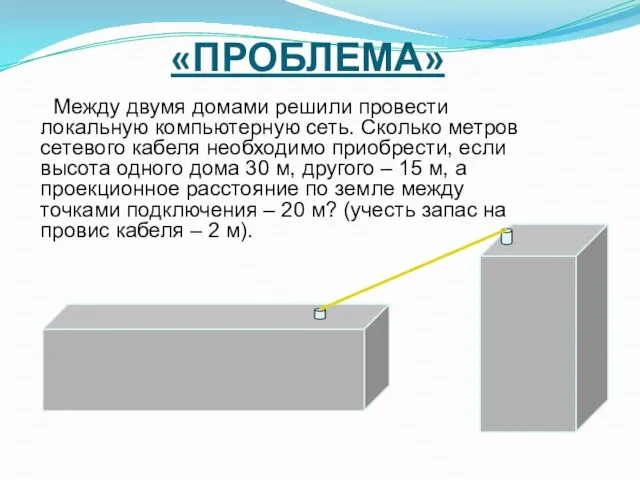
- 3. «ПРОБЛЕМА» Между двумя домами решили провести локальную компьютерную сеть. Сколько метров сетевого кабеля необходимо приобрести, если
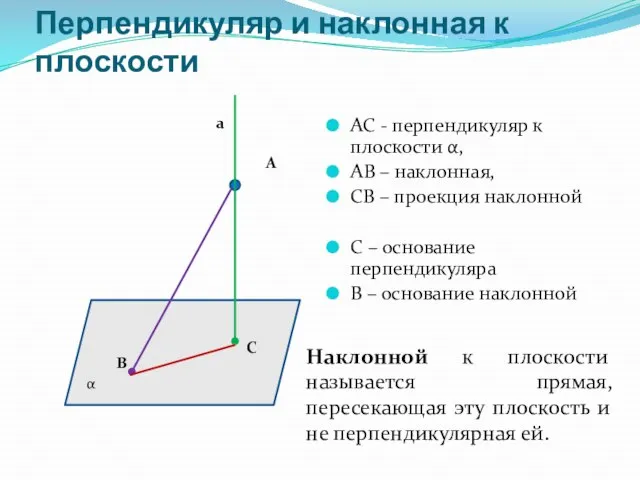
- 4. Перпендикуляр и наклонная к плоскости АС - перпендикуляр к плоскости α, АВ – наклонная, СВ –
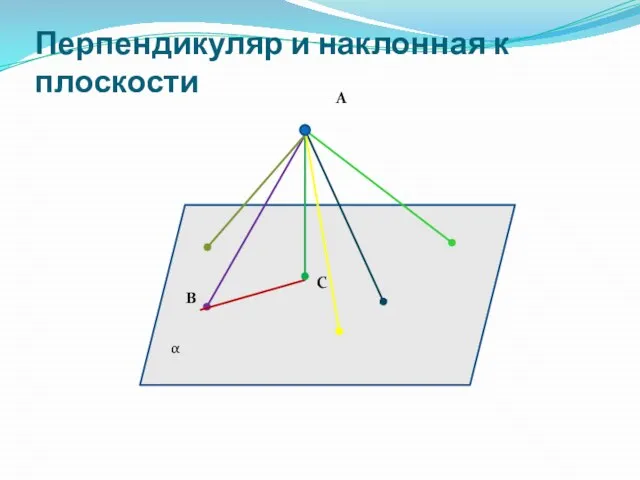
- 5. Перпендикуляр и наклонная к плоскости
- 6. Теорема о перпендикуляре и наклонной Перпендикуляр, опущенный из точки на плоскость, короче всякой наклонной, проведенной из
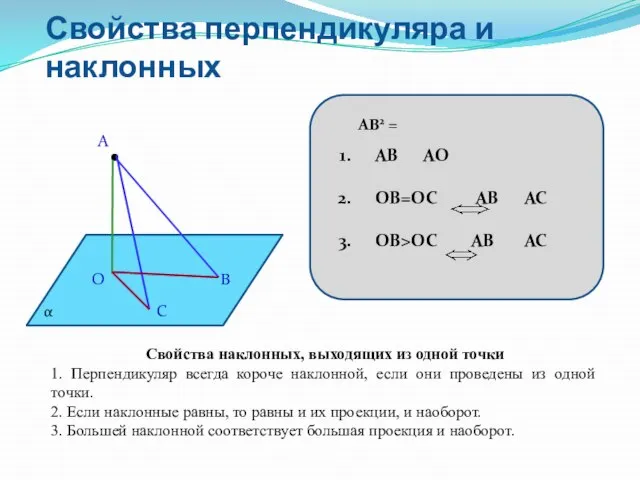
- 7. Свойства перпендикуляра и наклонных А В С О α АВ2 = Свойства наклонных, выходящих из одной
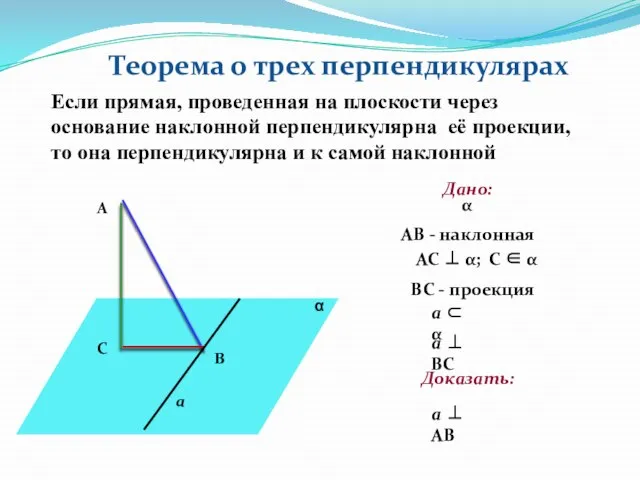
- 8. ВС - проекция Теорема о трех перпендикулярах Если прямая, проведенная на плоскости через основание наклонной перпендикулярна
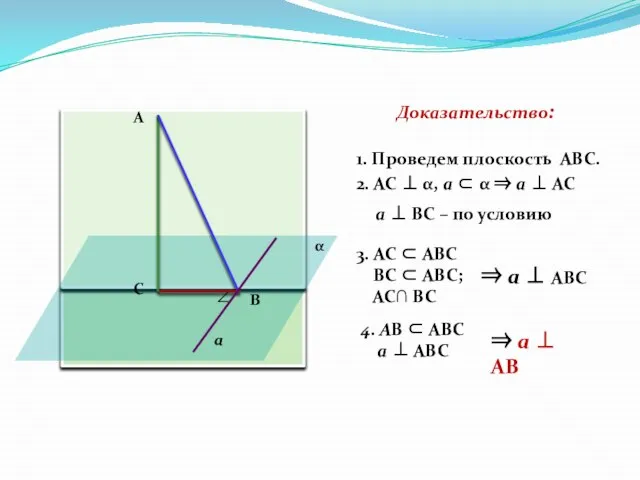
- 9. Доказательство: 1. Проведем плоскость AВС. 2. АС ⊥ α, a ⊂ α ⇒ a ⊥ АС
- 10. Задача Из точки A к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках
- 12. Скачать презентацию



 Площадь поверхности цилиндра
Площадь поверхности цилиндра Системы принятия решений. Оценки экстремума
Системы принятия решений. Оценки экстремума Дроби и проценты
Дроби и проценты Системы случайных величин
Системы случайных величин Предельные величины, эластичности
Предельные величины, эластичности Презентация на тему Построение графика функции методом ее исследования с помощью производной
Презентация на тему Построение графика функции методом ее исследования с помощью производной  Системы принятия решений. Алгоритмы оптимизации
Системы принятия решений. Алгоритмы оптимизации Уравнение плоскости
Уравнение плоскости Презентация на тему Устный счёт в пределах 10 (1 класс)
Презентация на тему Устный счёт в пределах 10 (1 класс)  Конструирование предметов из геометрических фигур
Конструирование предметов из геометрических фигур Решение задач
Решение задач Построение сечений тетраэдра параллелепипеда
Построение сечений тетраэдра параллелепипеда Логарифм произведения
Логарифм произведения Преобразование графиков функций. 8 класс
Преобразование графиков функций. 8 класс Сантиметр (см)
Сантиметр (см) Порядок действий в выражениях со скобками
Порядок действий в выражениях со скобками Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Математика вокруг нас. 10 класс
Математика вокруг нас. 10 класс Планиметрия и стериометрия
Планиметрия и стериометрия Приключения Буратино в Стране Финансов
Приключения Буратино в Стране Финансов Измеряй и сравнивай
Измеряй и сравнивай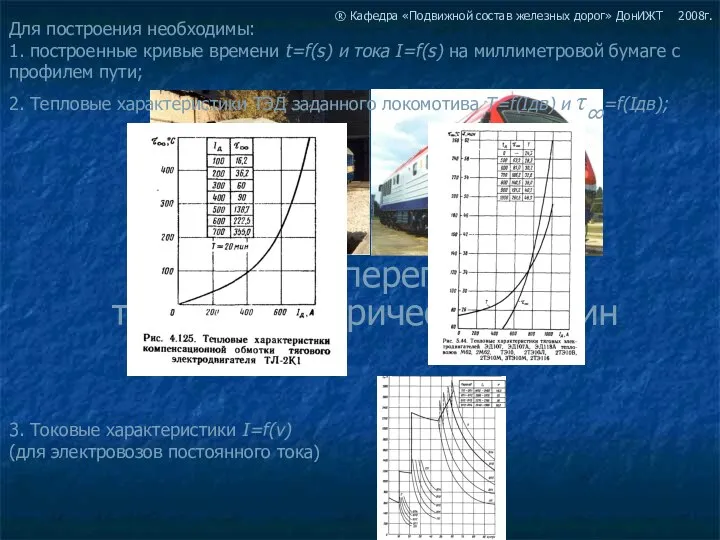 Расчет перегрева тяговых электрических машин
Расчет перегрева тяговых электрических машин Знакомство с линиями чертежа
Знакомство с линиями чертежа Смеси и сплавы в задачах №13 ЕГЭ-2015 г
Смеси и сплавы в задачах №13 ЕГЭ-2015 г Игра Поле чудес геометрия
Игра Поле чудес геометрия Математика + Информатика
Математика + Информатика Полиномы над полями конечной характеристики
Полиномы над полями конечной характеристики Множества (числовые и не только)
Множества (числовые и не только)