Перпендикуляр и наклонная. Угол между прямой и плоскостью

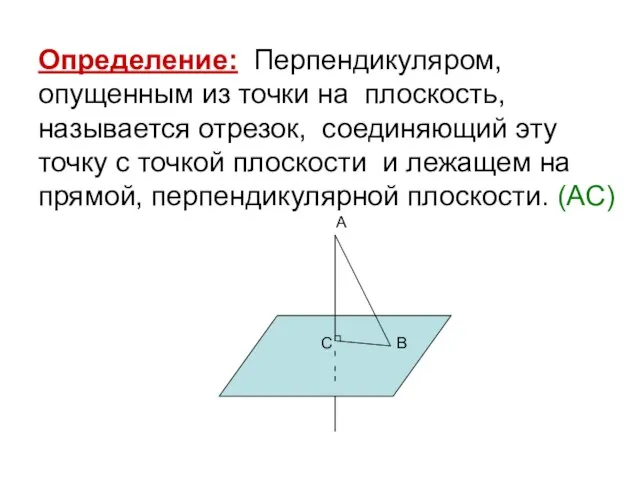
Определение: Перпендикуляром, опущенным из точки на плоскость, называется отрезок, соединяющий эту точку с точкой плоскости и лежащем на прямой, перпендикулярной плоскости. (АС)
А
С
В

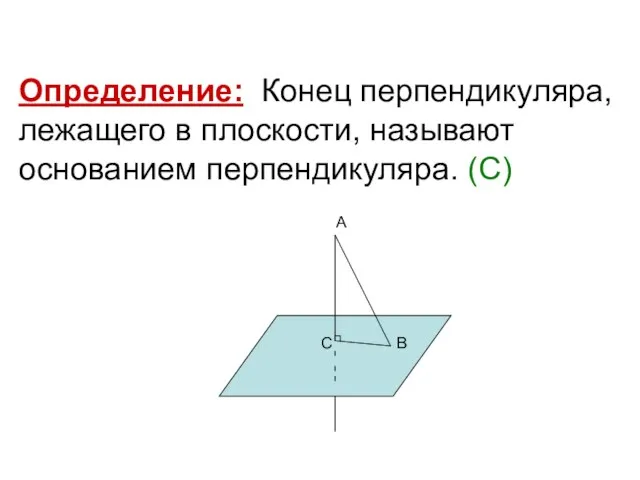
Определение: Конец перпендикуляра, лежащего в плоскости, называют основанием перпендикуляра. (С)
А
С
В

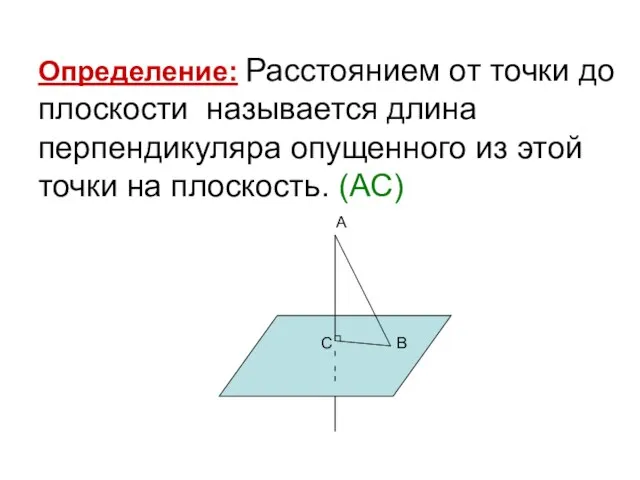
Определение: Расстоянием от точки до плоскости называется длина перпендикуляра опущенного из этой точки на плоскость. (АС)
А
С
В

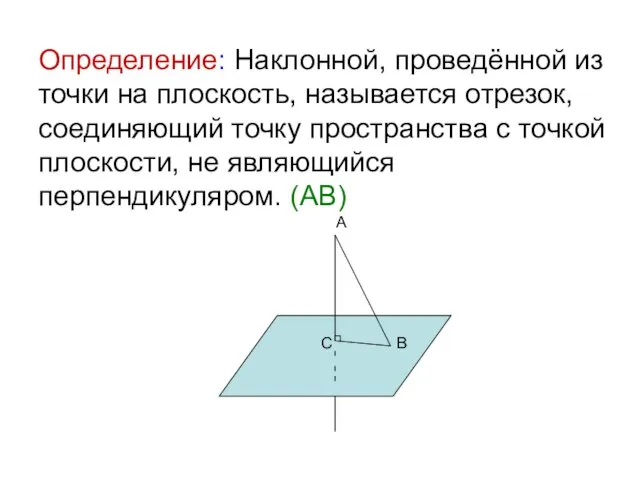
Определение: Наклонной, проведённой из точки на плоскость, называется отрезок, соединяющий точку пространства с точкой плоскости, не являющийся перпендикуляром. (АВ)
А
С
В

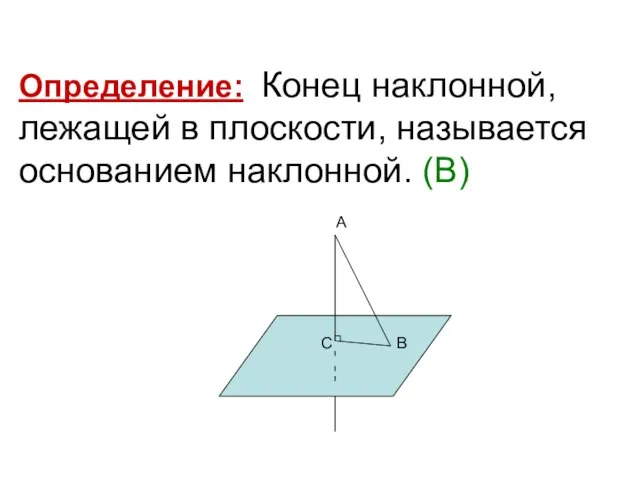
Определение: Конец наклонной, лежащей в плоскости, называется основанием наклонной. (В)
А
С
В

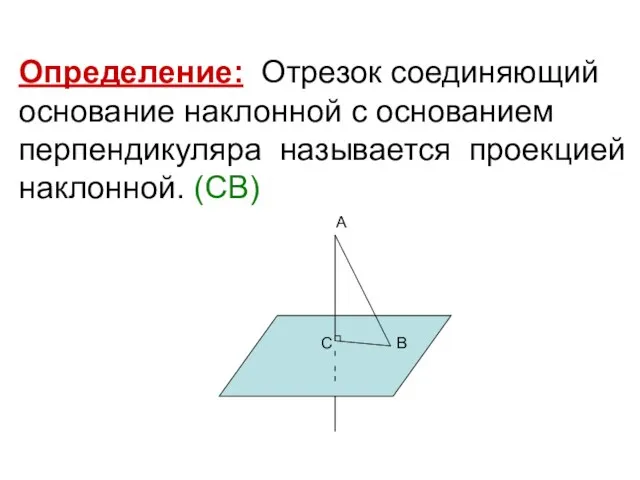
Определение: Отрезок соединяющий основание наклонной с основанием перпендикуляра называется проекцией наклонной. (СВ)
А
С
В

Свойства наклонной и проекции.
1. Равные наклонные имеют равные проекции.(Верно и обратное: Равные проекции имеют равные наклонные.)
2. Из двух неравных наклонных наибольшая имеет наибольшую проекцию.
3. Перпендикуляр меньше наклонной проведённой из одной точки к плоскости.

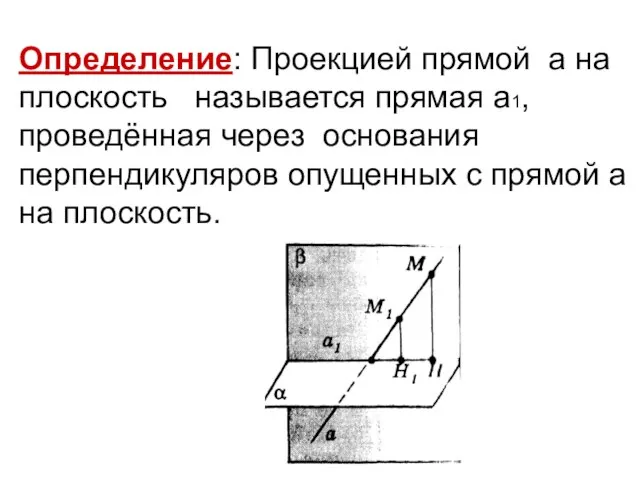
Определение: Проекцией прямой а на плоскость называется прямая а1, проведённая через основания перпендикуляров опущенных с прямой а на плоскость.

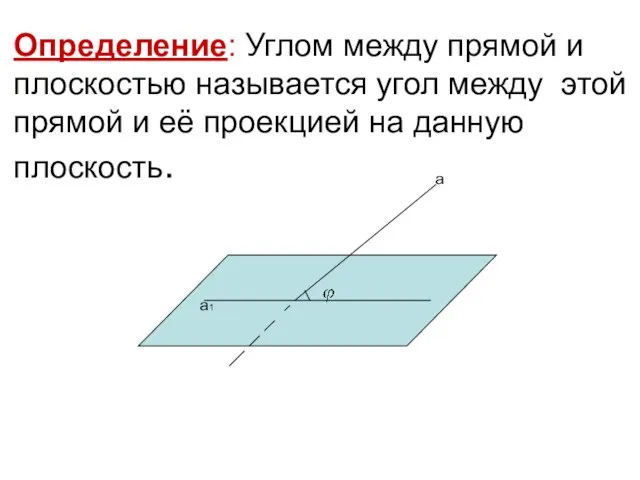
Определение: Углом между прямой и плоскостью называется угол между этой прямой и её проекцией на данную плоскость.
а
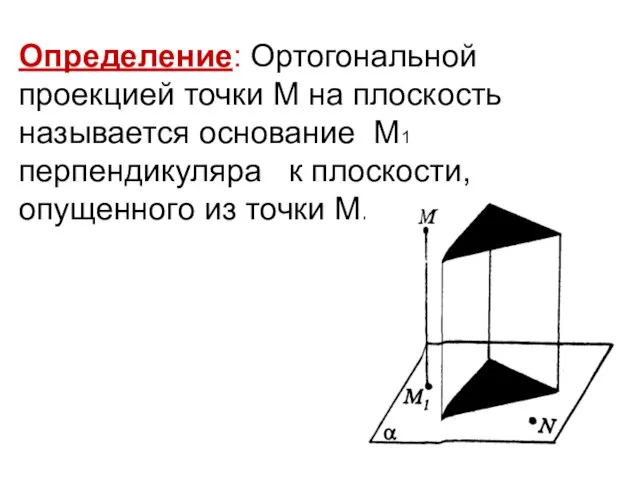
а1

Определение: Ортогональной проекцией точки М на плоскость называется основание М1 перпендикуляра к плоскости, опущенного из точки М.

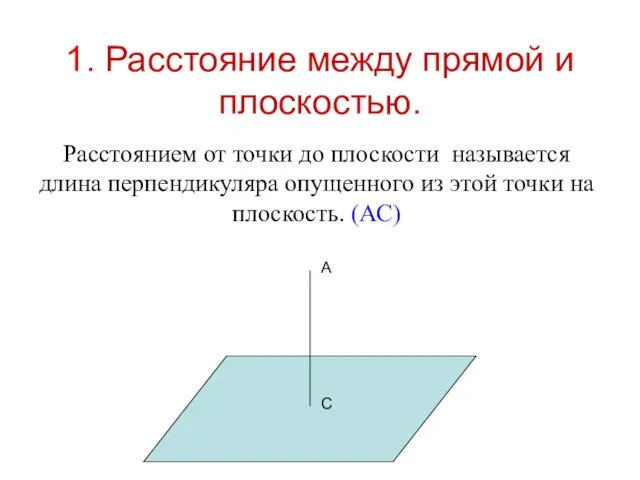
1. Расстояние между прямой и плоскостью.
Расстоянием от точки до плоскости называется длина перпендикуляра опущенного из этой точки на плоскость. (АС)
А
С

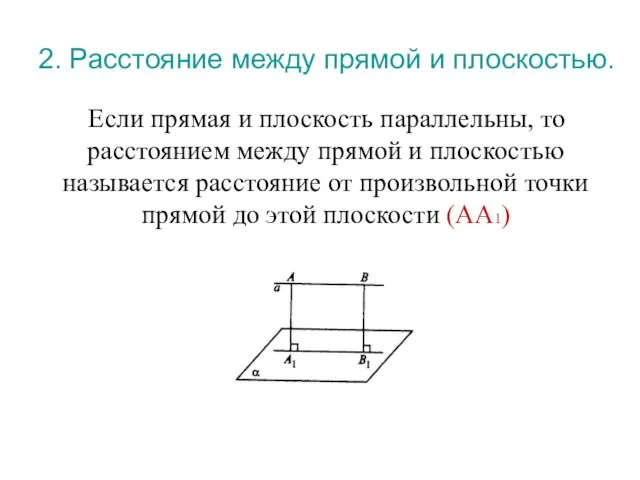
2. Расстояние между прямой и плоскостью.
Если прямая и плоскость параллельны, то расстоянием между прямой и плоскостью называется расстояние от произвольной точки прямой до этой плоскости (AA1)

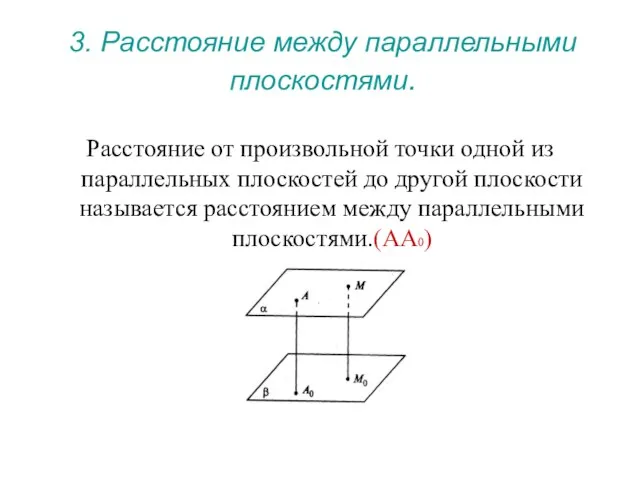
3. Расстояние между параллельными плоскостями.
Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.(AA0)

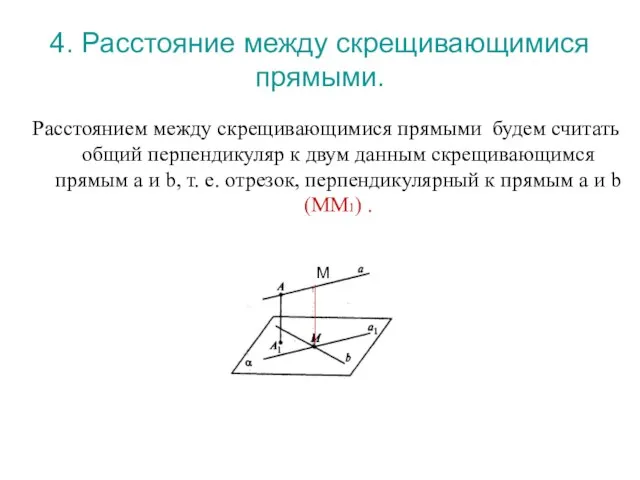
4. Расстояние между скрещивающимися прямыми.
Расстоянием между скрещивающимися прямыми будем считать общий перпендикуляр к двум данным скрещивающимся прямым а и b, т. е. отрезок, перпендикулярный к прямым а и b (ММ1) .
М

Теорема (о трёх перпендикулярах): Если прямая, проведённая в плоскости через основание наклонной, перпендикулярна к её проекции на эту плоскость, то она перпендикулярна и к самой наклонной.

Теорема (о трёх перпендикулярах): Обратная теорема: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.