Содержание
- 2. План: 1. Моделирование как метод научного познания 2. Классификация экономико-математических моделей 3. Этапы эконометрического моделирования
- 3. 1. Моделирование как метод научного познания Модель – это такой материальный или мысленно представляемый объект, который
- 4. Определения Математическая модель – это математические формулы, уравнения, неравенства, или их системы, которые с некоторой точностью
- 5. Определения Экономико-математические методы – это совокупность математических методов (математического программирования, теории вероятностей, теории массового обслуживания, теории
- 6. Определения Экономико-математическая модель – это концентрированное выражение общих взаимосвязей и закономерностей экономического явления в математической форме
- 7. Необходимость использования метода моделирования Необходимость использования метода моделирования определяется тем, что многие объекты непосредственно исследовать или
- 8. 2. Классификация экономико-математических моделей По целевому назначению экономико-математические модели делятся на теоретико-аналитические, используемые в исследованиях общих
- 9. Этапы построения эконометрических моделей 1. Постановочный. Формулируется цель исследования (анализ, прогноз, управленческое решение), определяются экономические переменные
- 10. Основные формулы комбинаторики Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично
- 11. Перестановки Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только
- 12. Пример 1 Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит
- 13. Размещения Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом
- 14. Пример 2 Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если каждая
- 15. Сочетания Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы
- 16. Пример 3 В группе 6 студентов. Из них нужно избрать двух студентов для участия в студенческой
- 17. Повторение испытаний
- 18. Независимые испытания Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от
- 19. Независимые испытания Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо
- 20. Формула Бернулли Производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и
- 21. Пример 4 Вероятность появления события А в каждом испытании равна 0,75. Найти вероятность того, что в
- 22. Локальная теорема Лапласа Если вероятность появления события А в каждом испытании постоянна и равна р, то
- 23. Пример 5 Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если
- 24. Решение n=400; k=80; p=0,2; q=0,8.
- 25. Интегральная теорема Лапласа Если вероятность появления события А в каждом испытании постоянна и равна р, то
- 26. Задание Скачать файл «Практическое занятие 2» из MOODLE и выполнить приведенные задания Решение задания загрузить в
- 28. Скачать презентацию

























 Делители и кратные
Делители и кратные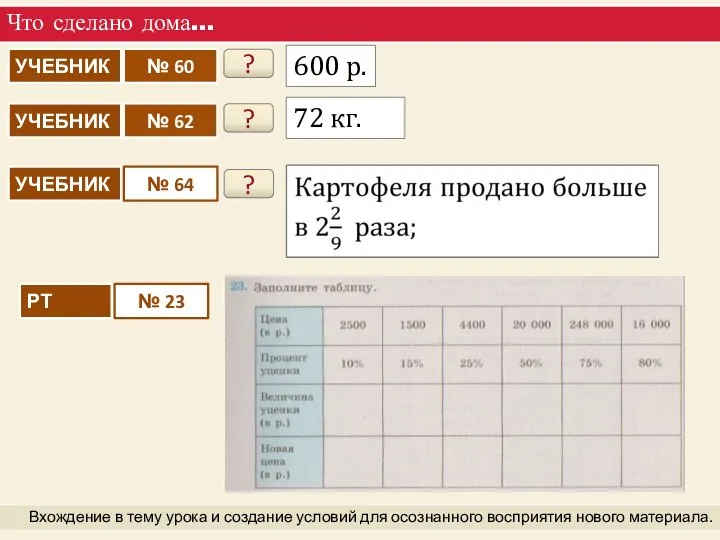 Решение задач на проценты
Решение задач на проценты Презентация на тему Измерение углов
Презентация на тему Измерение углов  Пирамиды
Пирамиды Парная регрессия и корреляция. Тема 2
Парная регрессия и корреляция. Тема 2 Примеры
Примеры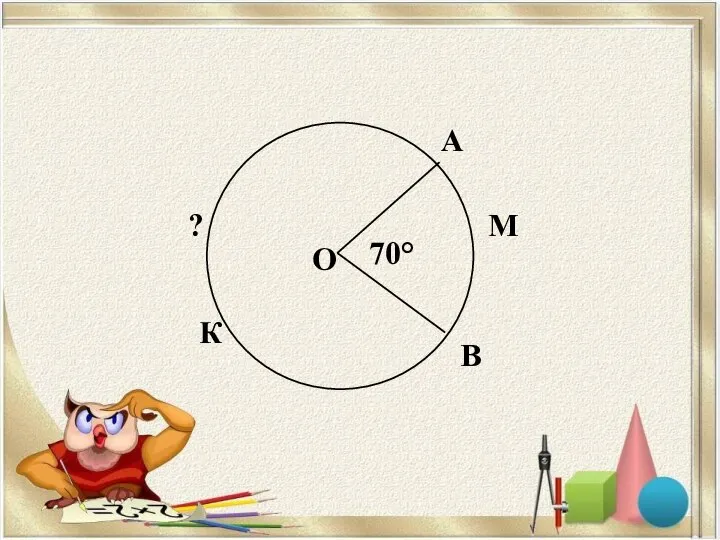 Окружность. Вписанные и описанные углы
Окружность. Вписанные и описанные углы Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам Комплексные числа. Понятие мнимой единицы
Комплексные числа. Понятие мнимой единицы Весеннее приключение. Займемся математикой
Весеннее приключение. Займемся математикой قدرمطلقی درجه اول
قدرمطلقی درجه اول Пропорциональность величин
Пропорциональность величин Ромб. Квадрат
Ромб. Квадрат Числовые промежутки
Числовые промежутки Исследование функций с помощью производных. Правила Лопиталя
Исследование функций с помощью производных. Правила Лопиталя Многоугольники
Многоугольники Исследовательская работа по теме: Конус и его применение в быту
Исследовательская работа по теме: Конус и его применение в быту Выражение в инфиксной форме. Выражение в постфиксной форме
Выражение в инфиксной форме. Выражение в постфиксной форме Первообразная. Неопределенный интеграл и его свойства
Первообразная. Неопределенный интеграл и его свойства Отделение математических наук РАН
Отделение математических наук РАН Презентация на тему Лист Мебиуса
Презентация на тему Лист Мебиуса  Признаки параллельности прямых
Признаки параллельности прямых Презентация на тему Пентамино
Презентация на тему Пентамино 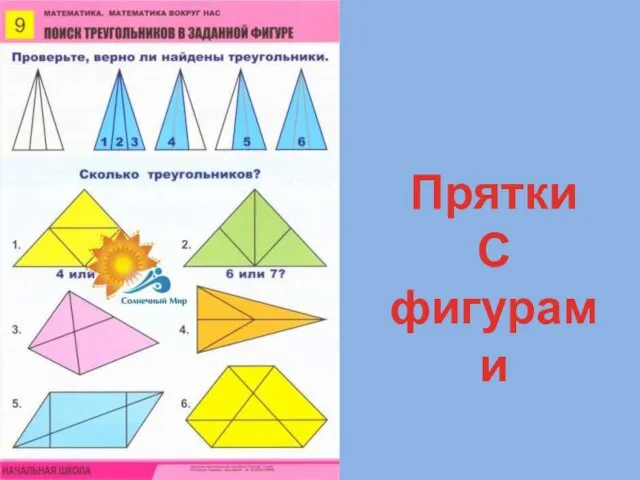 Прятки с фигурами
Прятки с фигурами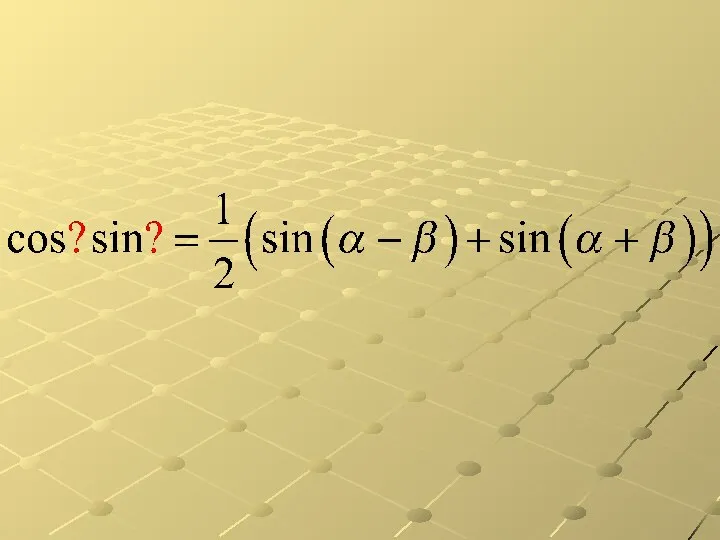 Тригонометрические формулы. Диктант
Тригонометрические формулы. Диктант Помогают законы. 5 - 7 класс
Помогают законы. 5 - 7 класс Дифференциальное исчисление функции одной переменной
Дифференциальное исчисление функции одной переменной Каких чисел не бывает
Каких чисел не бывает