Содержание
- 2. О, математика, ты вечна! Гордись, прекрасная, собой! Твоё величье бесконечно, Так предначертано судьбой! Всегда овеяна ты
- 3. Древний Египет Самый большой, сохранившийся до наших дней, древнеегипетский математический текст – это так называемый папирус
- 4. Задача из папируса Ахмеса Приходит пастух с 70 быками. Его спрашивают: - Сколько приводишь ты из
- 5. Китай. Возникновение китайской цивилизации на берегах реки Хуанхэ относится к началу II тыс. до н. э.
- 6. Задача древнего Китая (II век н.э.) Дикая утка от южного моря до северного моря летит 7
- 7. Индия. В I тысячелетии н. э. индийские учёные изобрели знакомую нам десятичную систему записи чисел. Ими
- 8. Задача Древней Индии Брахмагупта, Индия, около 600 г. Слон, слониха и слонёнок пришли к озеру, чтобы
- 9. Решение: Слон - 1 озеро 3ч 10 озёр 30ч Слониха- 1 озеро 5ч 6 озёр 30
- 10. Страны Ислама Крупнейшие ученые средневековья – ал-Хорезми, Авиценна, ал-Бируни, Омар Хайям, ал-Каши писали свои сочинения на
- 11. Задачи стран Ислама В знаменитой книге «1001 ночь» мудрец задаёт юной деве следующую задачу: Одна женщина
- 12. Решение: I способ: 1) 1-1/2=1/2(ч) осталась 2) 1/2-1/4=1/4(ч) осталась 3) 1/4-1/8=1/8(ч) осталась 4) 1/8-1/16=1/16(ч) осталась 1/16
- 13. Древняя Греция. Если от математики Древнего Востока до нас дошли отдельные задачи с решениями и таблицы,
- 14. Задача Древней Греции Из Акмимского папируса (VI в.) Некто взял из сокровищницы 1/13. Из того, что
- 15. Герон Александрийский ( I в. н. э.) Задача: Бассейн может заполняться через четыре фонтана. Если открыть
- 16. Россия. Первые сведения о развитие математики на Руси относится к IX – XII вв. (древнерусская нумерация,
- 17. Первый российский учебник по математике — «Арифметика» Л. Ф. Магницкого, изданный в 1703 году. Эта книга,
- 18. Лошадь съедает воз сено за месяц, коза- за два месяца, овца- за три месяца. За какое
- 19. Четыре плотника хотят построить дом. Первый плотник может построить дом за год, второй- за 2 года,
- 21. Скачать презентацию


















 Урок математики 13.09
Урок математики 13.09 Многогранники. Решение задач
Многогранники. Решение задач Презентация на тему Прибавление и вычитание числа 3
Презентация на тему Прибавление и вычитание числа 3  Прямые и плоскости в пространстве
Прямые и плоскости в пространстве Деление круглых сотен на число 100
Деление круглых сотен на число 100 Рациональные дроби и их свойства
Рациональные дроби и их свойства Признаки равенства треугольников
Признаки равенства треугольников Решение уравнений, содержащих параметры
Решение уравнений, содержащих параметры Числа - близнецы
Числа - близнецы Логарифмическая функция, ее свойства и график
Логарифмическая функция, ее свойства и график Решение задач на проценты. Урок - сказка
Решение задач на проценты. Урок - сказка Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников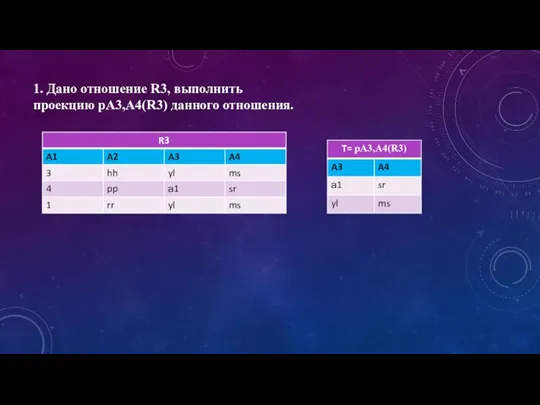 Дано отношение R3, выполнить проекцию pA3,A4(R3) данного отношения
Дано отношение R3, выполнить проекцию pA3,A4(R3) данного отношения Углы в пространстве. Перпендикулярность плоскостей
Углы в пространстве. Перпендикулярность плоскостей Числовые последовательности
Числовые последовательности Решение линейных уравнений
Решение линейных уравнений Вычисление пределов функции в точке
Вычисление пределов функции в точке Цифра 10
Цифра 10 Основные фигуры планиметрии
Основные фигуры планиметрии Презентация на тему Математический диктант (4 класс)
Презентация на тему Математический диктант (4 класс)  Выбор схемы измерения переменных
Выбор схемы измерения переменных Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Урок математики 3 класс
Урок математики 3 класс Десятки, единицы, цифры
Десятки, единицы, цифры Построение графиков функций. Алгебра и начала анализа 11 класс
Построение графиков функций. Алгебра и начала анализа 11 класс Дискретные случайные величины
Дискретные случайные величины Дерево возможных вариантов
Дерево возможных вариантов Презентация на тему В царстве квадратных корней
Презентация на тему В царстве квадратных корней