Содержание
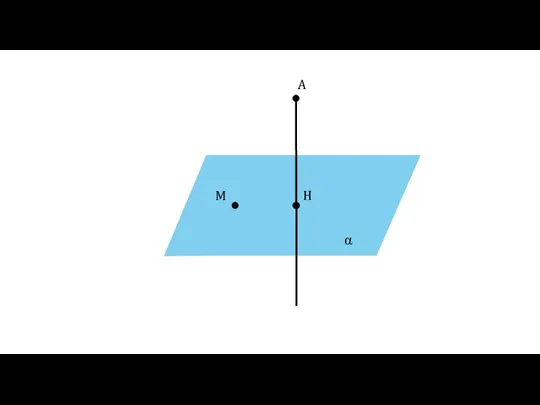
- 2. α A H M
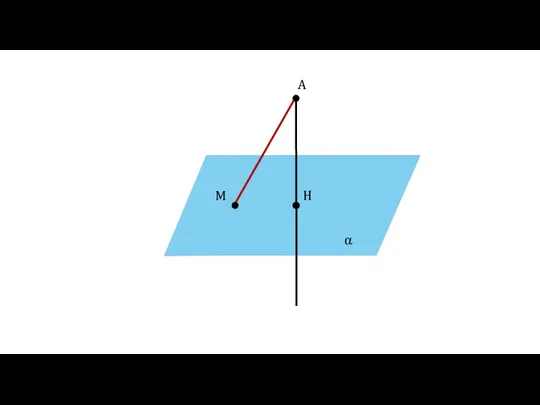
- 3. α A H M
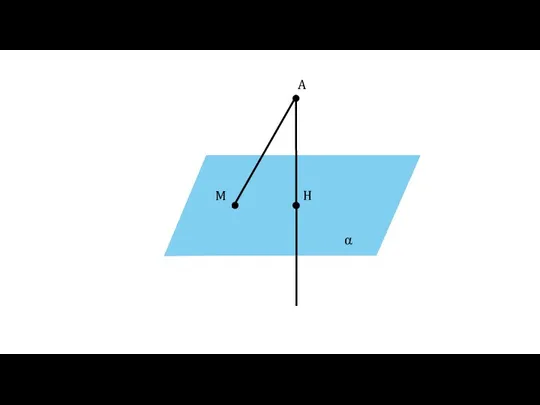
- 4. α A H M
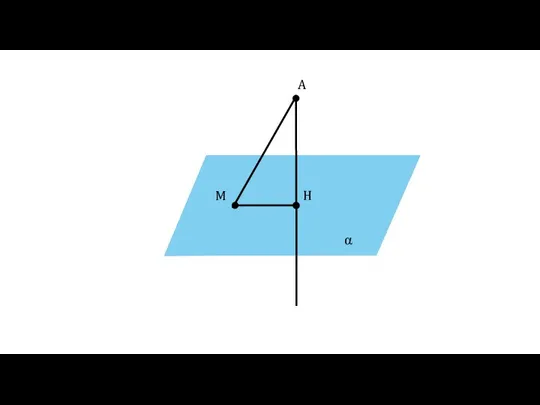
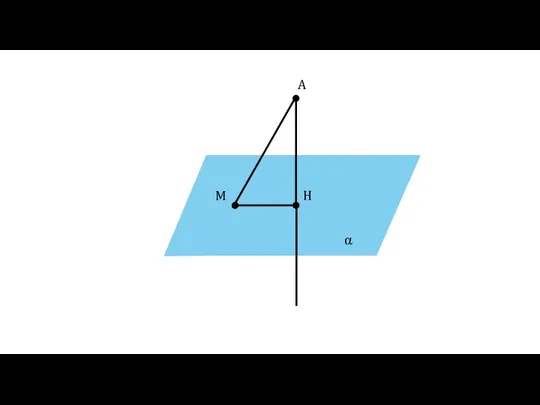
- 5. Определение Отрезок АМ называется наклонной, проведённой из точки А к плоскости α. Точка М называется основанием
- 6. α A H M
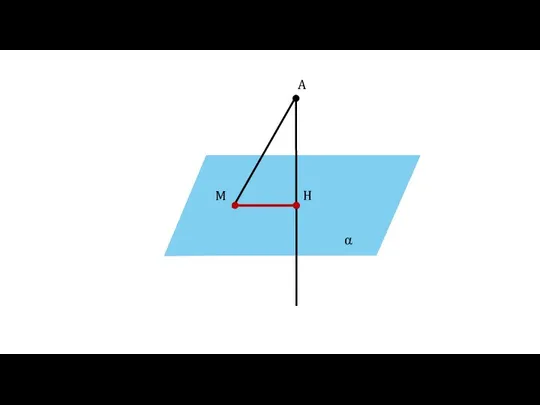
- 7. α A H M
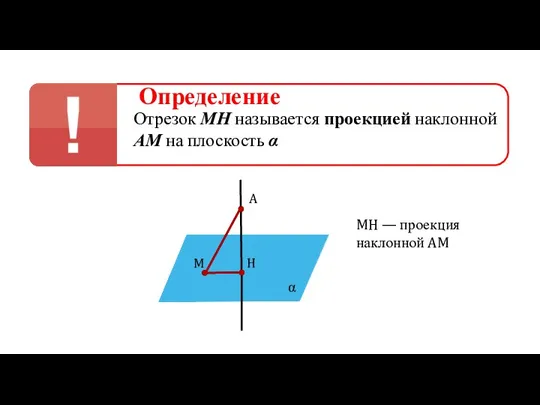
- 8. Определение Отрезок МН называется проекцией наклонной АМ на плоскость α α A H M MH —
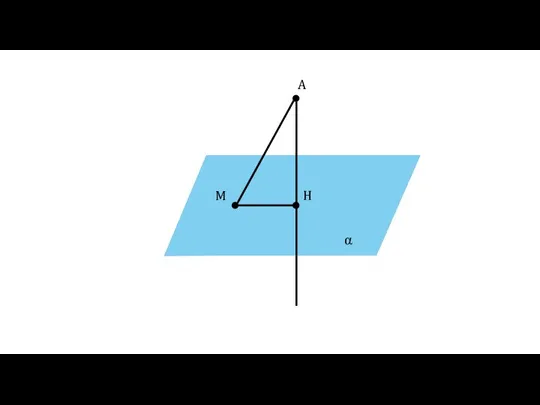
- 9. α A H M
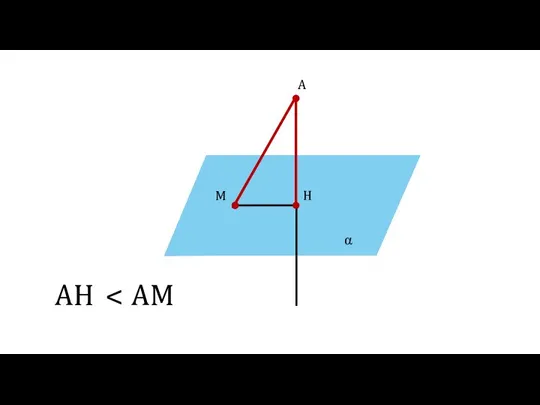
- 10. α A H M AH AM
- 11. α A H M
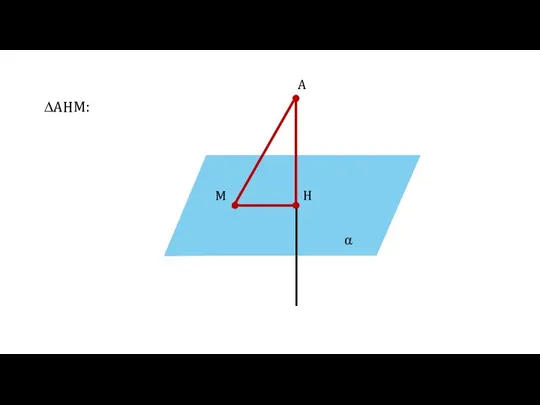
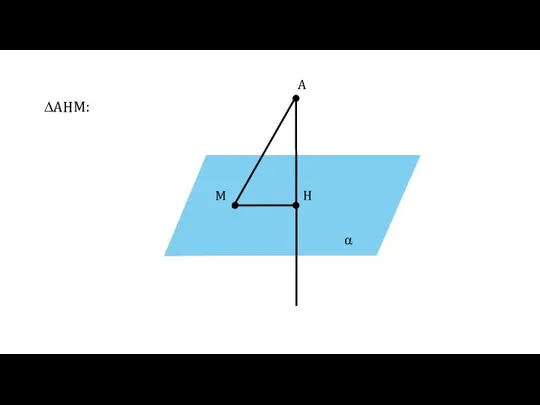
- 12. α A H M ∆AHM:
- 13. α A H M ∆AHM:
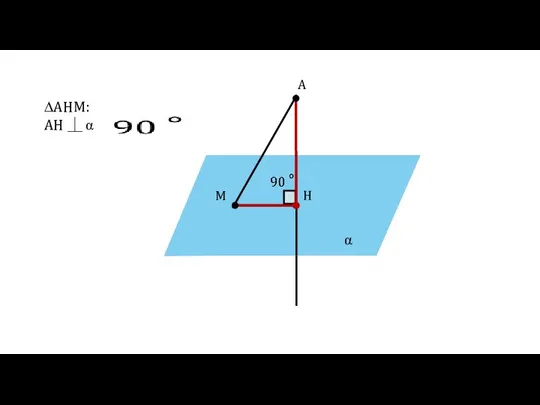
- 14. α A H M ∆AHM: AH ⏊ α
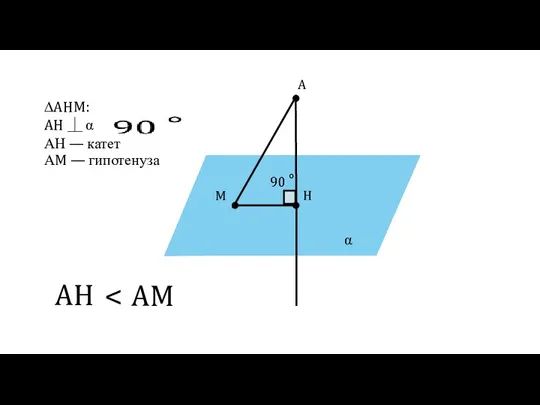
- 15. α A H M ∆AHM: AH ⏊ α AH AM АН — катет АM — гипотенуза
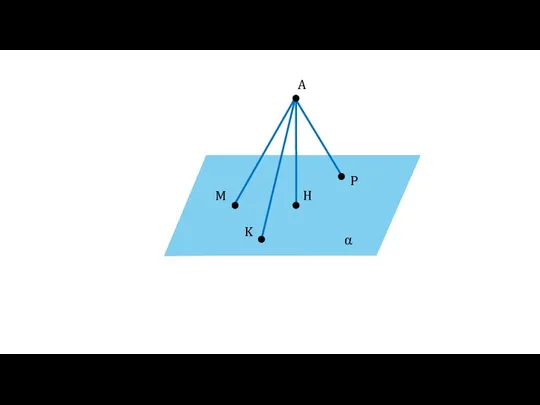
- 16. α A H M P K
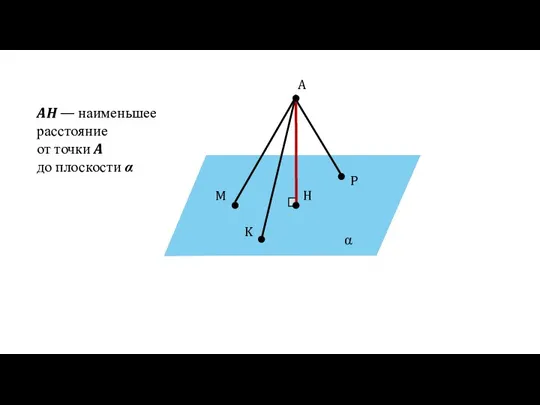
- 17. α A H M P K AH — наименьшее расстояние от точки A до плоскости α
- 18. Определение Расстоянием от точки А до плоскости α называется длина перпендикуляра АН, проведённого к плоскости α
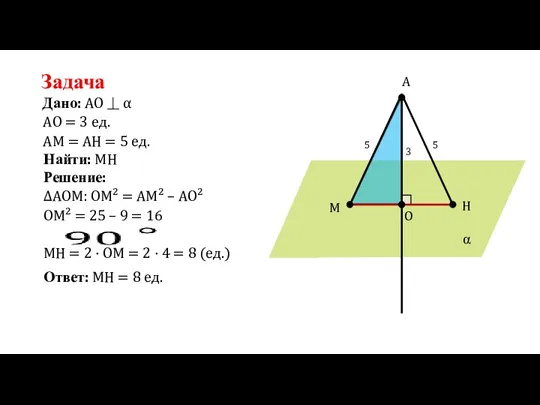
- 19. Задача Дано: AO = 3 ед. AO ⏊ α α A O M H 3 AM
- 20. Задание
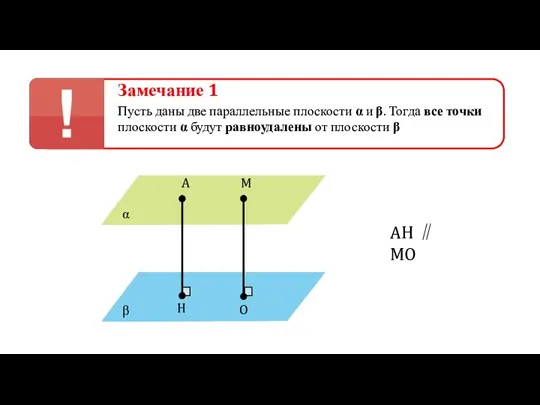
- 21. Замечание 1 Пусть даны две параллельные плоскости α и β. Тогда все точки плоскости α будут
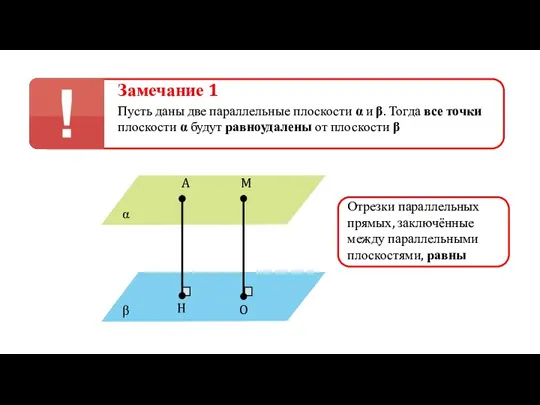
- 22. Замечание 1 Пусть даны две параллельные плоскости α и β. Тогда все точки плоскости α будут
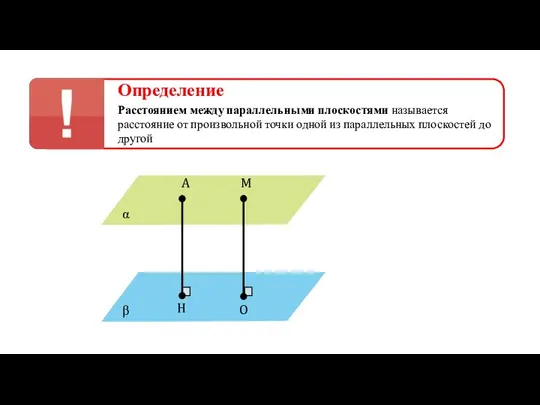
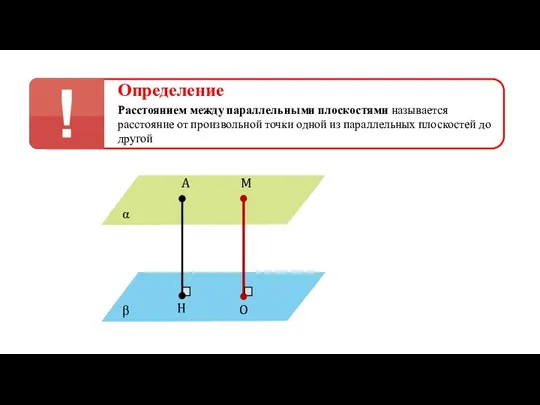
- 23. Определение Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой
- 24. Определение Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой
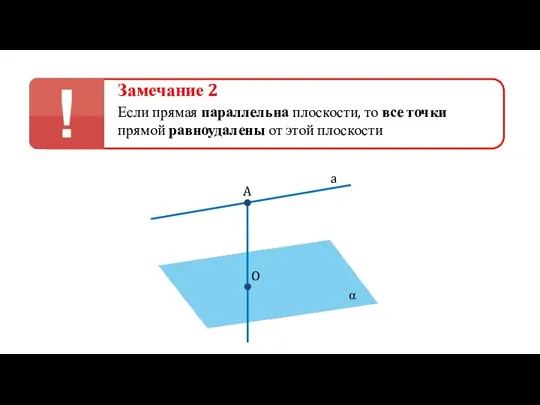
- 25. Замечание 2 Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости a A
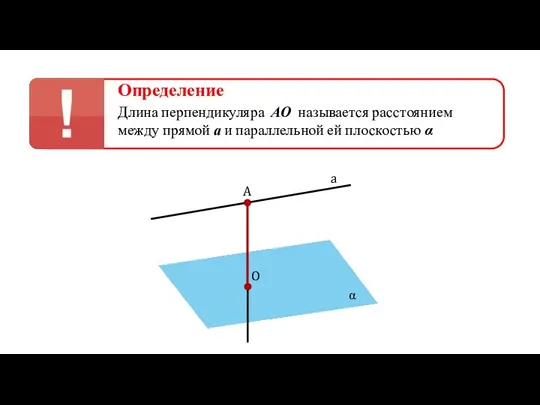
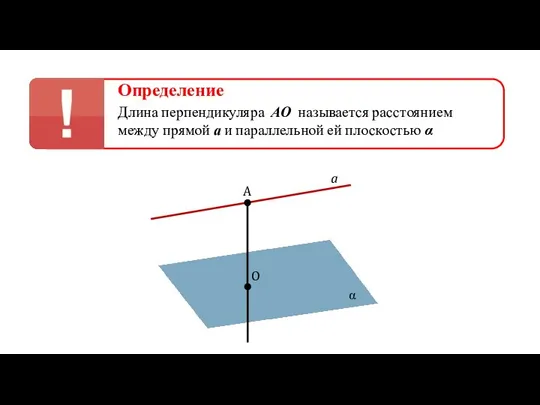
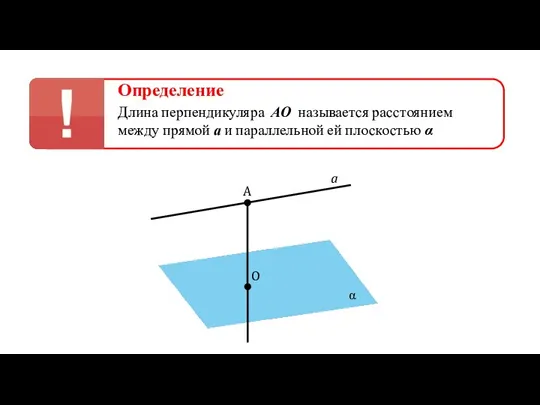
- 26. Определение Длина перпендикуляра АО называется расстоянием между прямой а и параллельной ей плоскостью α a A
- 27. Определение Длина перпендикуляра АО называется расстоянием между прямой а и параллельной ей плоскостью α a A
- 28. Определение Длина перпендикуляра АО называется расстоянием между прямой а и параллельной ей плоскостью α a A
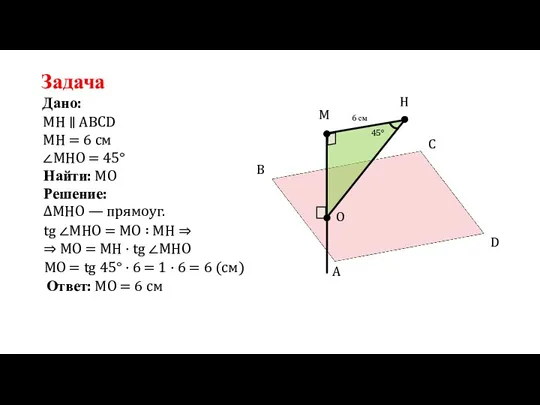
- 29. A Задача Дано: МН ∥ ABCD H M O B C D МН = 6 см
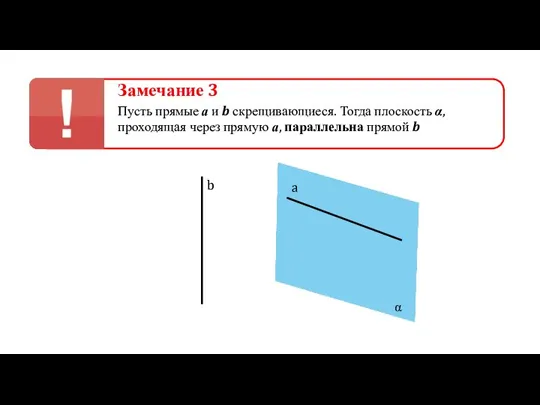
- 30. Замечание 3 Пусть прямые а и b скрещивающиеся. Тогда плоскость α, проходящая через прямую а, параллельна
- 32. Скачать презентацию



 Степень с натуральным показателем
Степень с натуральным показателем Теоремы косинусов и синусов
Теоремы косинусов и синусов Смешанные числа
Смешанные числа Построение сечений
Построение сечений Что узнали? Чему научились?
Что узнали? Чему научились? Теория вероятности. Сокращение дробей
Теория вероятности. Сокращение дробей Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Разбиение множеств на классы
Разбиение множеств на классы Неопределенный интеграл
Неопределенный интеграл Задача з піцою
Задача з піцою Множества
Множества Натуральные числа. Демонстрационный материал. 5 класс
Натуральные числа. Демонстрационный материал. 5 класс Основные этапы исследования элементарных функций
Основные этапы исследования элементарных функций Корни. Формулы
Корни. Формулы Презентация на тему Решение задач на нахождение неизвестного по двум разностям
Презентация на тему Решение задач на нахождение неизвестного по двум разностям  Проверка деления
Проверка деления Площадь параллелограмма
Площадь параллелограмма Решение выражений и уравнений
Решение выражений и уравнений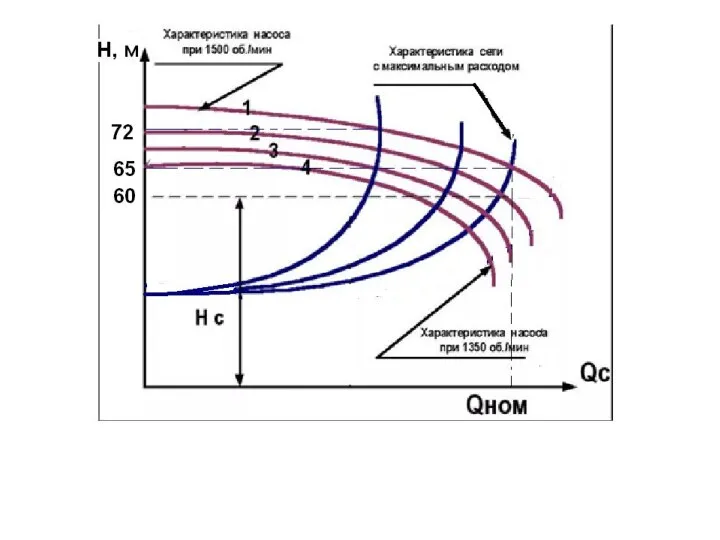 Модель частотно-регулируемого привода. (Тема 8)
Модель частотно-регулируемого привода. (Тема 8) Умножение и деление смешанных чисел
Умножение и деление смешанных чисел Арифметические действия с десятичными дробями. Математический тренажёр
Арифметические действия с десятичными дробями. Математический тренажёр Презентация на тему Производная функции
Презентация на тему Производная функции  Презентация на тему ГИА 2013. Модуль «Алгебра» №1
Презентация на тему ГИА 2013. Модуль «Алгебра» №1  Проце́нт. Происхождение процентов
Проце́нт. Происхождение процентов Презентация на тему Наибольшее и наименьшее значения функции
Презентация на тему Наибольшее и наименьшее значения функции  Презентация на тему ГИА 2013. Модуль АЛГЕБРА №7
Презентация на тему ГИА 2013. Модуль АЛГЕБРА №7  Метод неопределенных коэффициентов
Метод неопределенных коэффициентов Теорема, обратная теореме Пифагора
Теорема, обратная теореме Пифагора