Первообразная F'(x) = f(x)

Содержание урока:
F'(x) = f(x)
Определение первообразной
F(x)+C = ∫f(x)dx
Неоднозначность первообразной
Нахождение первообразных в простейших случаях
Проверка первообразной на заданном промежутке

Устные упражнения

Взаимно-обратные операции в математике
Прямая
Обратная
x2
Возведение в квадрат
sin α = a
Синус угла
arcsin a = α a∈[-1;1]
Арксинус числа
(xn)' = nxn-1
Дифференцирование
∫nxn-1dx = xn + C
Интегрирование

Пояснение в сравнении
Производная
"Производит" новую ф-ию
Первообразная
Первичный образ
дифференцирование
вычисление производной
интегрирование
восстановление функции из производной

Определение первообразной
y = F(x) называют первообразной для y = f(x) на промежутке X, если при x ∈ X
F'(x) = f(x)

Неоднозначность первообразной
f(x) = 2x
F1(x) = x2
F2(x) = x2 + 1
F3(x) = x2 + 5
F1'(x) = 2x
F2'(x) = 2x
F3'(x) = 2x
y = f(x) имеет бесконечно много первообразных вида y = F(x)+C, где
C - произвольное число

Определение интеграла
Если у функции y = f(x) на промежутке X есть первообразная y = F(x), то все множества функций вида y = F(x)+C называют
неопределенным интегралом от функции
y = f(x)
Обозначается как ∫f(x)dx
неопределенный интеграл f (эф) от x (икс) d (дэ) x (икс)

Правила интегрирования

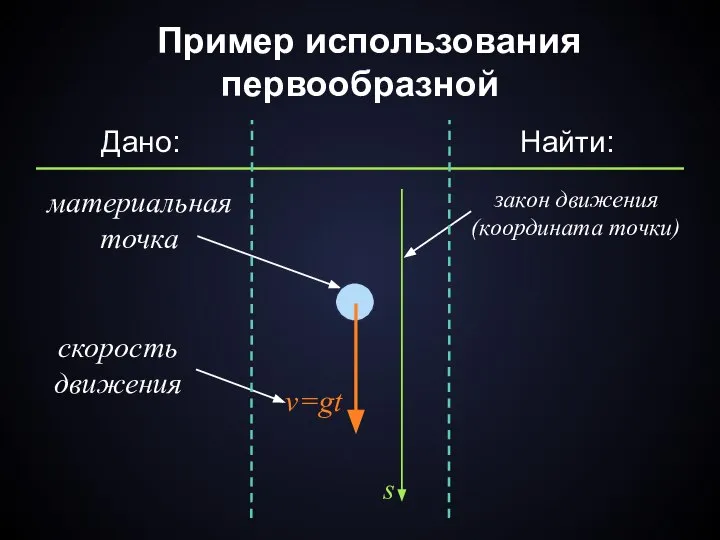
Пример использования первообразной
материальная точка
v=gt
скорость
движения
s
Дано:
Найти:
закон движения
(координата точки)

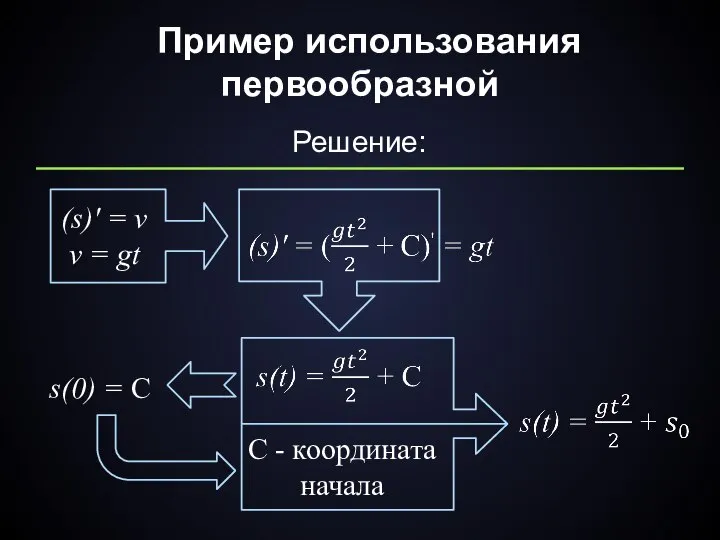
Пример использования первообразной
Решение:
(s)' = v
v = gt
s(0) = C
C - координата начала

Отработка материала
Практические задания

Найти одну из первообразных для следующих функций
1) f(x) = 4
2) f(x) = -1
3) f(x) = x3
4) f(x) = sin x
5) f(x) = x2 + 3cos x

Док-ть, что F(x) первообразная для f(x) на заданном промежутке
Условия
Дано: F(x) = 3x4
Док-ть: f(x) = 12x3
при x ∈ (-∞;+∞)
Доказательство
Найдем производную F(x): F'(x) = (3x4)' = 12x3 = f(x)
F'(x) = f(x), значит
F(x) = 3x4 первообразная для f(x) = 12x3