parallelnost_1

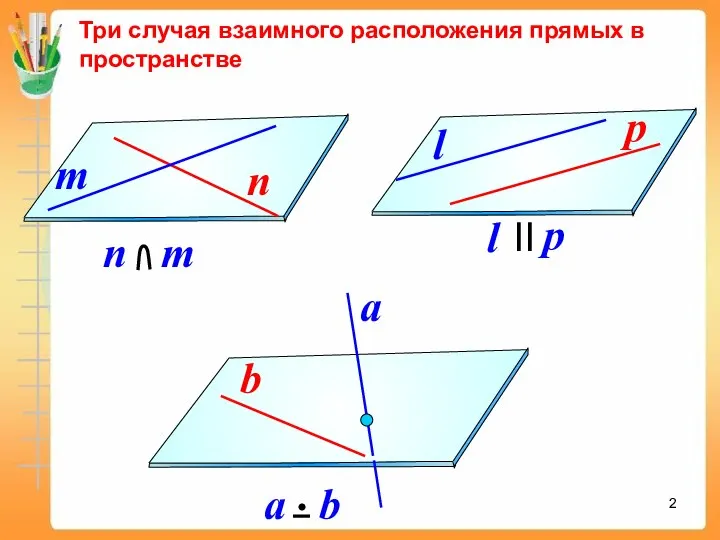
Три случая взаимного расположения прямых в пространстве

Планиметрия
Стереометрия
Две прямые на плоскости называются параллельными, если они не пересекаются.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
aIIb
aIIb

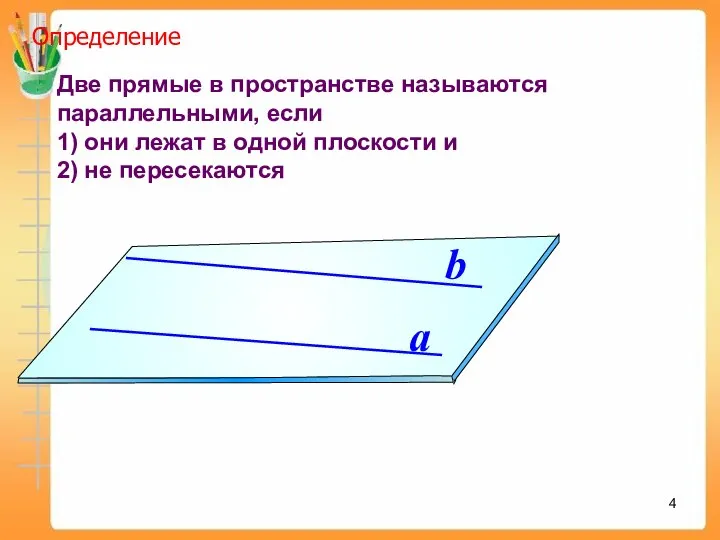
Две прямые в пространстве называются параллельными, если
1) они лежат в одной плоскости и
2) не пересекаются
a
b
Определение

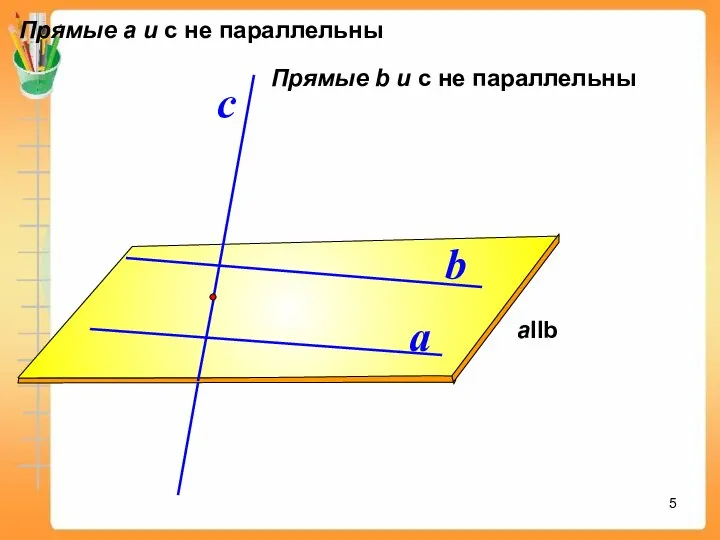
a
b
aIIb
с
Прямые а и с не параллельны
Прямые b и с не параллельны

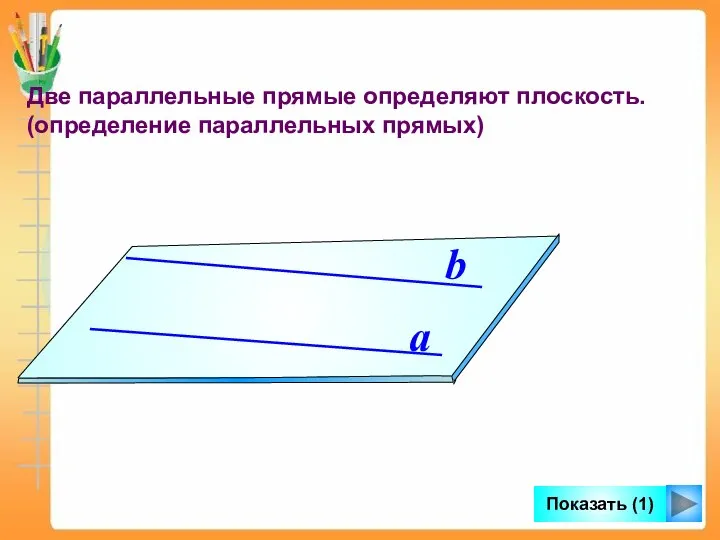
Две параллельные прямые определяют плоскость.
(определение параллельных прямых)
a
b
Показать (1)

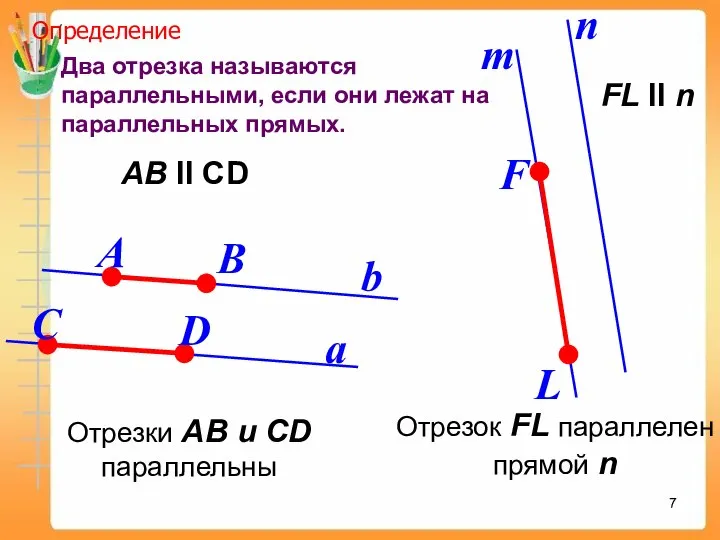
Два отрезка называются параллельными, если они лежат на параллельных прямых.
a
b
Определение
АВ II СD
FL II n
Отрезок FL параллелен
прямой n
Отрезки АВ и СD параллельны

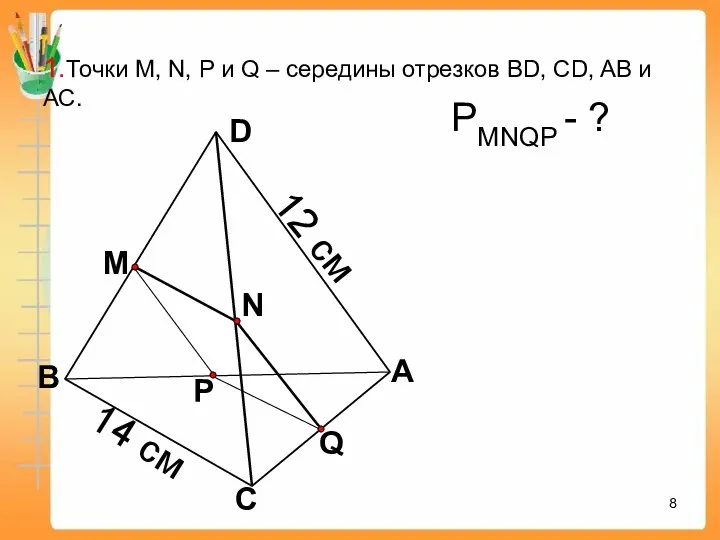
Q
А
С
В
D
N
M
P
1.Точки М, N, P и Q – середины отрезков BD, CD, AB и АС.
РMNQP - ?
12 см
14 см

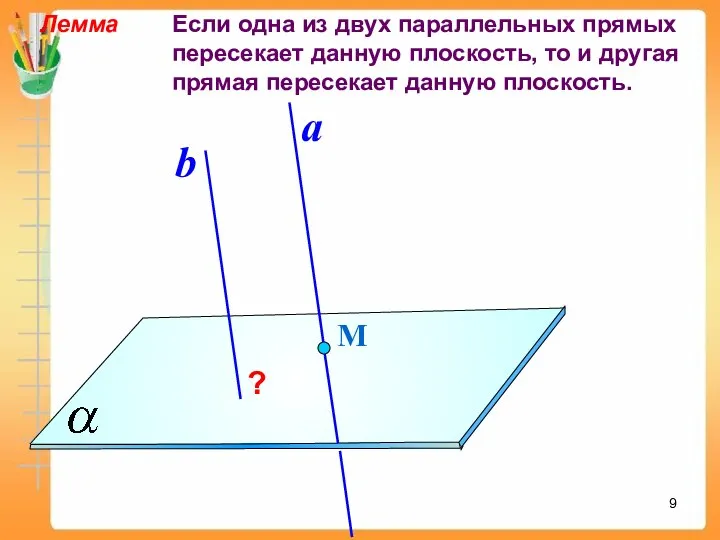
Лемма
Если одна из двух параллельных прямых
пересекает данную плоскость, то и другая
прямая пересекает данную плоскость.
М
a
?

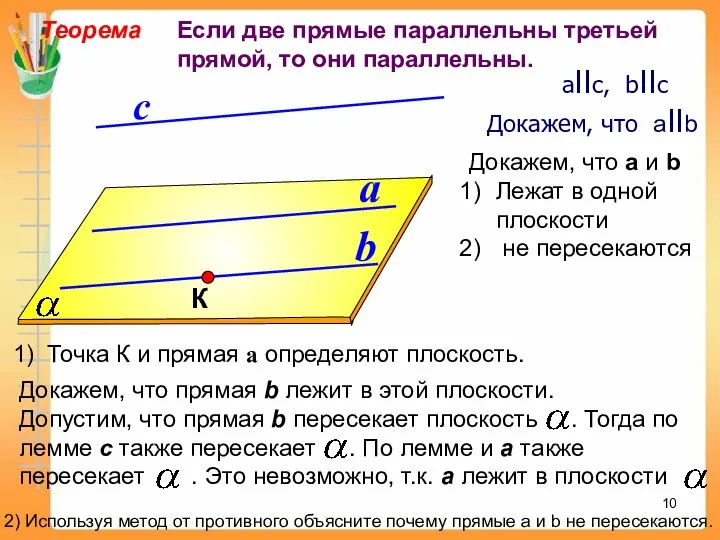
a
b
с
Теорема
Если две прямые параллельны третьей прямой, то они параллельны.
aIIс, bIIс
Докажем, что aIIb
1) Точка К и прямая а определяют плоскость.
Докажем, что а и b
Лежат в одной плоскости
не пересекаются
2) Используя метод от противного объясните почему прямые а и b не пересекаются.

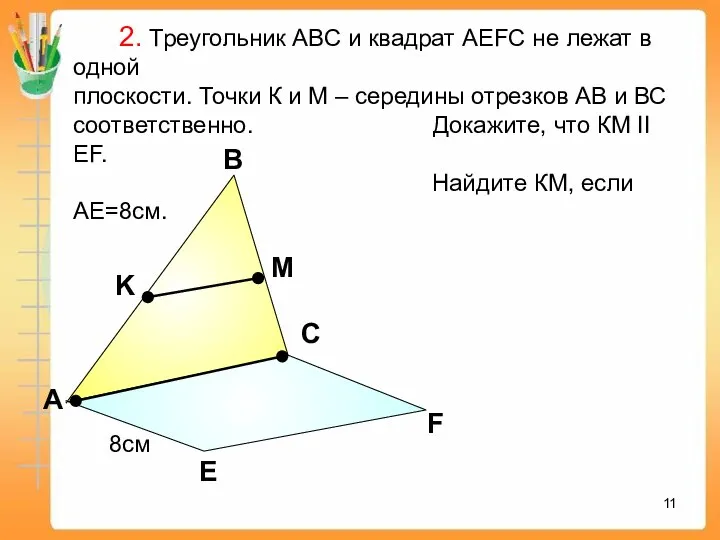
А
В
С
Е
F
K
M
2. Треугольник АВС и квадрат АEFC не лежат в одной
плоскости. Точки К и М – середины отрезков АВ и ВС соответственно. Докажите, что КМ II EF.
Найдите КМ, если АЕ=8см.
8см