сделать возможной операцию извлечения квадратного корня из любого действительного числа. Это, однако, не является достаточным основанием для того, чтобы вводить в математику новые числа. Оказалось, что если производить вычисления по обычным правилам над выражениями, в которых встречаются квадратный корень из отрицательного числа, то можно прийти к результату, уже не содержащему квадратный корень
из отрицательного числа. В XVI в.
Кардано нашел формулу для решения кубического уравнения. Оказалось, когда кубическое уравнение имеет три действительных корня, в формуле Кардано встречается квадратный корень из отрицательного числа.
Впервые, по-видимому, мнимые величины появились в известном труде «Великое искусство, или об алгебраических правилах» Кардано (1545), который счёл их непригодными к употреблению.













 Решение заданий типа № 21 ОГЭ
Решение заданий типа № 21 ОГЭ Конус. Основные элементы конуса
Конус. Основные элементы конуса Приложение по математике
Приложение по математике Презентация на тему Квадратные уравнения. Основные свойства
Презентация на тему Квадратные уравнения. Основные свойства  Презентация на тему Решение систем неравенств (9 класс)
Презентация на тему Решение систем неравенств (9 класс)  Практикумы по задачам на готовых чертежах
Практикумы по задачам на готовых чертежах Презентация на тему Определение конуса
Презентация на тему Определение конуса  Одночлены
Одночлены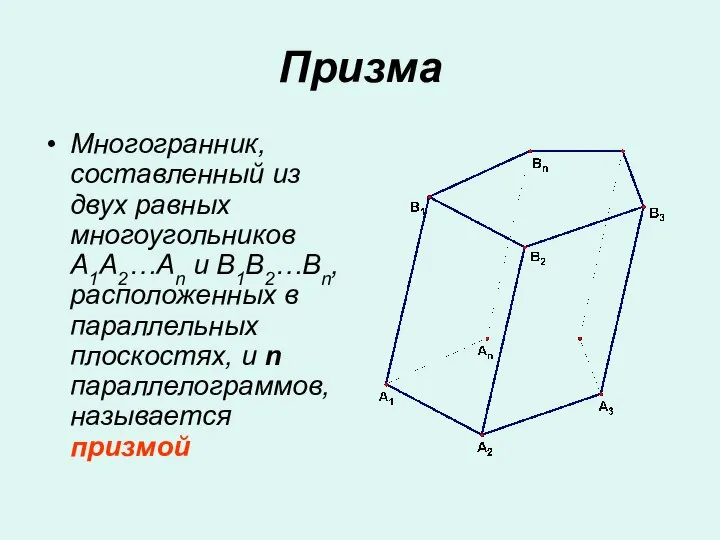 Призма. Боковые ребра призмы
Призма. Боковые ребра призмы Вероятность события есть количественная мера возможности наступления этого события
Вероятность события есть количественная мера возможности наступления этого события Теория вероятностей
Теория вероятностей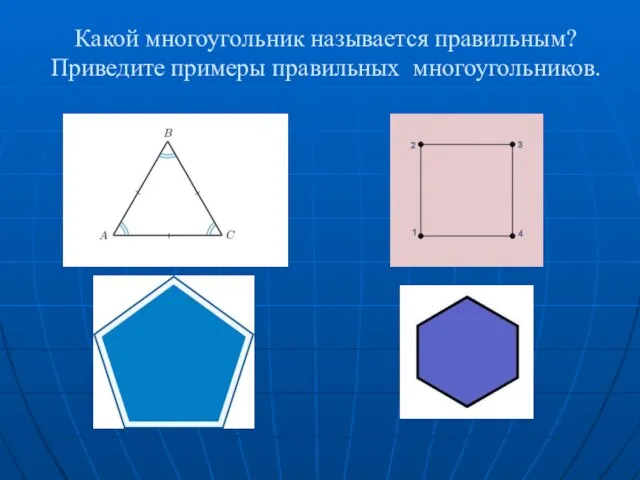 Какой многоугольник называется правильным? Приведите примеры правильных многоугольников
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников Урок математики с элементами театрализации
Урок математики с элементами театрализации Решение систем неравенств
Решение систем неравенств Развертка поверхностей геометрических тел
Развертка поверхностей геометрических тел Проекты сезона 2020-21
Проекты сезона 2020-21 Пересекающиеся и параллельные прямые
Пересекающиеся и параллельные прямые Текстовые задачи
Текстовые задачи Цифра 10
Цифра 10 Приёмы сложения в пределах 10
Приёмы сложения в пределах 10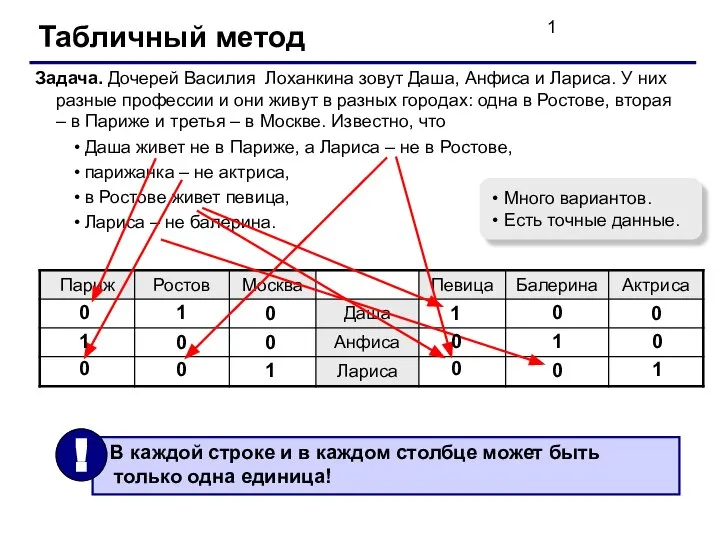 Табличный метод решения логических задач
Табличный метод решения логических задач Треугольники. Подобие треугольников
Треугольники. Подобие треугольников Сочетательное и распределительное свойства умножения
Сочетательное и распределительное свойства умножения Прямые на плоскости
Прямые на плоскости Плоскость в пространстве
Плоскость в пространстве Презентация на тему Прямая и точка
Презентация на тему Прямая и точка  Путешествие по океану Математики
Путешествие по океану Математики Теорема Пифагора
Теорема Пифагора