Ключевые задачи по теме пирамида

ГЛАВНЫЙ ВОПРОС В ЗАДАЧАХ С ПИРАМИДОЙ
Где находится основание высоты ?

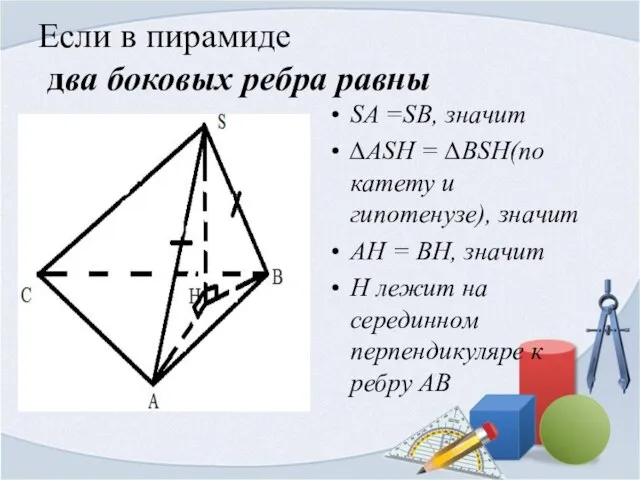
Если в пирамиде
два боковых ребра равны
SA =SB, значит
∆ASH = ∆BSH(по катету и гипотенузе), значит
AH = BH, значит
H лежит на серединном перпендикуляре к ребру АВ

Если в пирамиде
два боковых ребра равны
два боковых ребра равнонаклонены к плоскости основания
два боковых ребра составляют с высотой пирамиды равные углы
то основание высоты лежит на
серединном перпендикуляре к общему ребру основания

Если в пирамиде
Все боковые ребра равны
Все боковые ребра равнонаклонены к плоскости основания
Все боковые ребра составляют с высотой пирамиды равные углы
то основание высоты лежит
в центре описанной окружности

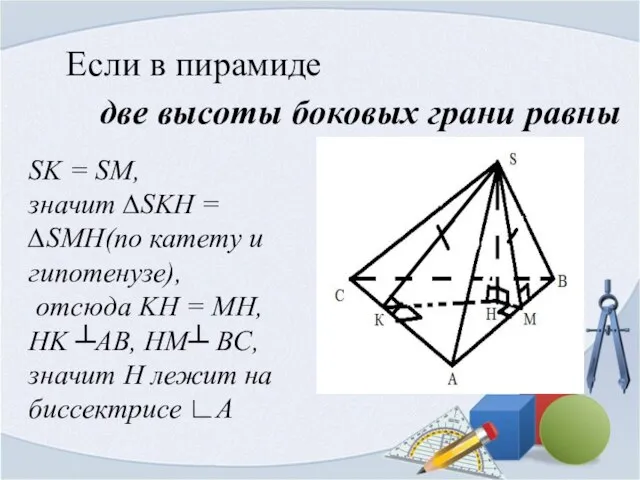
Если в пирамиде
две высоты боковых грани равны
SK = SM,
значит ∆SKH = ∆SMH(по катету и гипотенузе),
отсюда KH = MH, HK ┴AB, HM┴ BC,
значит Н лежит на биссектрисе ∟А

Если в пирамиде
два двугранных угла при основании равны
две высоты боковых грани равны
боковое ребро составляет равные углы с ребрами основания
то основание высоты лежит на
биссектрисе общего угла основания

Если в пирамиде
Все двугранные углы при основании равны
Все высоты боковых грани равны
Все боковые ребра составляют равные углы с ребрами основания
то основание высоты лежит на
в центре вписанной окружности