Содержание
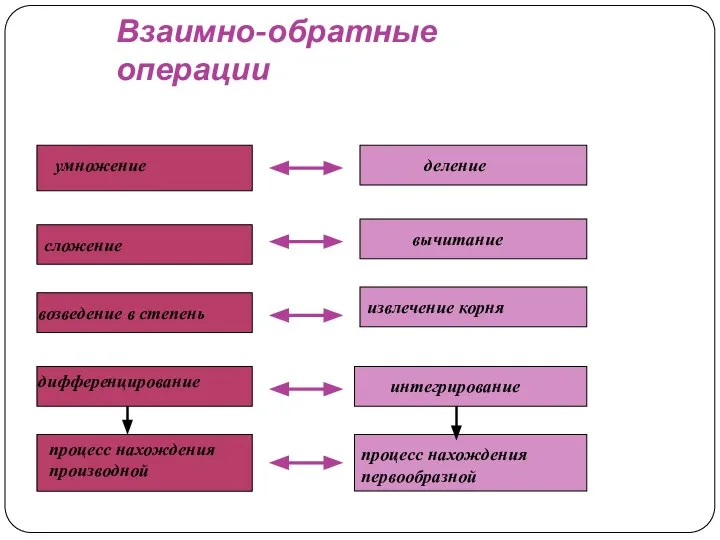
- 2. умножение деление сложение вычитание возведение в степень извлечение корня дифференцирование интегрирование Взаимно-обратные операции процесс нахождения производной
- 3. Первообразной для функции f(x) называется функция, производная которой равна данной Определение первообразной Функция F(x) называется первообразной
- 4. Таблица первообразных некоторых функций
- 5. Основное свойство первообразных Если F(x) – первообразная функции f(x), то и функция F(x)+C, где C –
- 6. Найти производную функции F(x): Вывод: для данной функции существует множество первообразных, их можно записать в виде
- 7. Найти первообразную функций
- 8. Неопределенный интеграл Совокупность всех первообразных данной функции f(x) называется ее неопределенным интегралом и обозначается : ,
- 9. Правила интегрирования
- 10. Свойства интеграла, вытекающие из определения Производная неопределенного интеграла равна подынтегральной функции, а его дифференциал- подынтегральному выражению.
- 11. Таблица неопределенных интегралов
- 12. Таблица неопределенных интегралов
- 13. Примеры
- 14. Примеры
- 16. Скачать презентацию












 Уравнение прямой
Уравнение прямой Знакомство с образованием чисел второго десятка
Знакомство с образованием чисел второго десятка Методы интегрирования. Непосредственное интегрирование
Методы интегрирования. Непосредственное интегрирование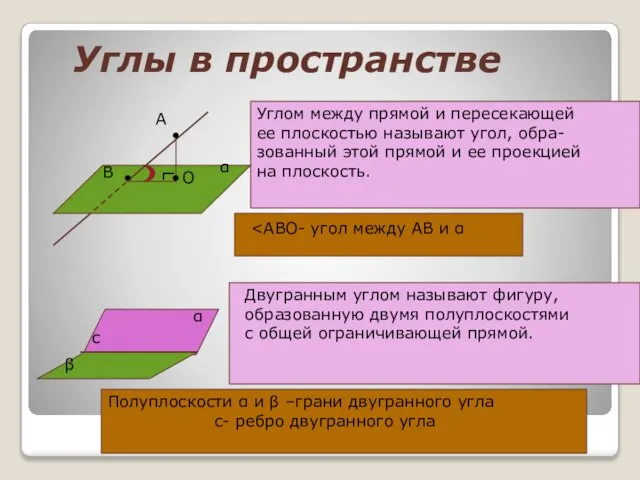 Двугранный угол. Угол между плоскостями. Перпендикулярность двух плоскостей
Двугранный угол. Угол между плоскостями. Перпендикулярность двух плоскостей Таблицы по алгебре
Таблицы по алгебре Непрерывность функций. Точки разрыва
Непрерывность функций. Точки разрыва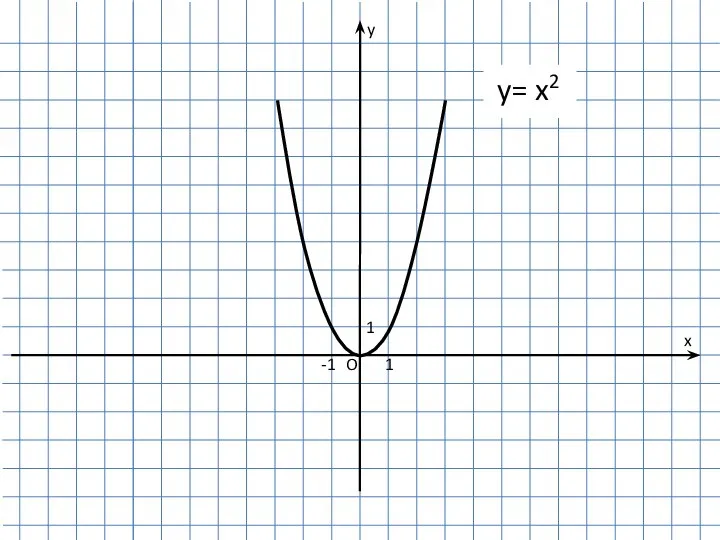 Преобразование графиков функции
Преобразование графиков функции Презентация на тему Разложение многочлена на множители с помощью комбинации различных приемов
Презентация на тему Разложение многочлена на множители с помощью комбинации различных приемов 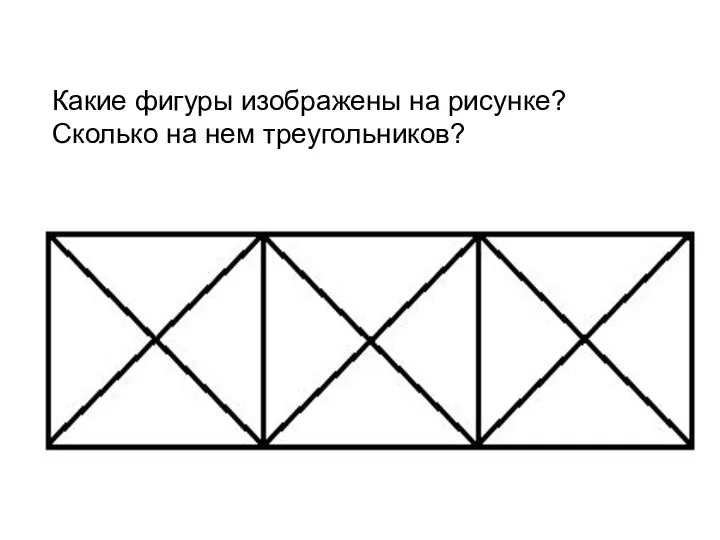 Периметр треугольника
Периметр треугольника Линейная алгебра, теория вероятностей и математический анализ
Линейная алгебра, теория вероятностей и математический анализ Случаи вычитания 15 -
Случаи вычитания 15 -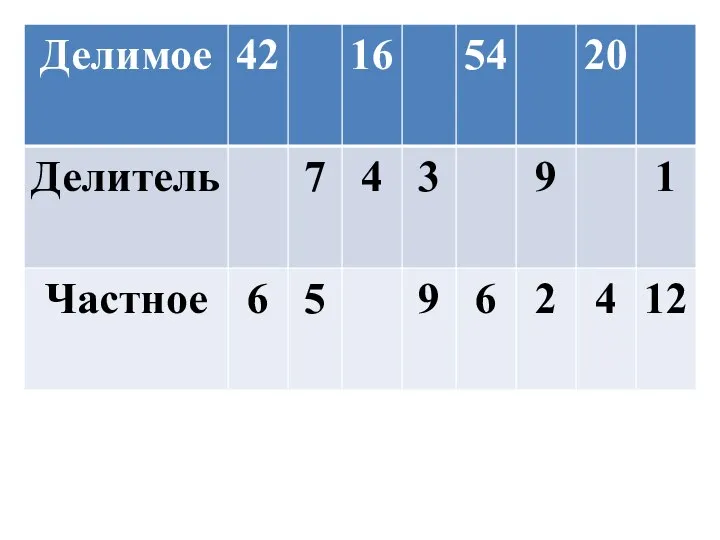 Таблица умножения и деления
Таблица умножения и деления Арккосинус а. Решение уравнений
Арккосинус а. Решение уравнений Основные свойства логарифмов
Основные свойства логарифмов Область определения функции
Область определения функции Свойства степени с натуральным показателем. 9 класс
Свойства степени с натуральным показателем. 9 класс Урок геометрии в 8 классе по теме Площадь
Урок геометрии в 8 классе по теме Площадь Векторная алгебра
Векторная алгебра Названия чисел в записях действий
Названия чисел в записях действий Презентация на тему Целое и части (1 класс)
Презентация на тему Целое и части (1 класс)  Презентация на тему Движение фигур в стереометрии
Презентация на тему Движение фигур в стереометрии  Симметрия в Алтайских орнаментах на примере алтайских костюмов
Симметрия в Алтайских орнаментах на примере алтайских костюмов Теория пределов. Понятие предела. Предел функции в точке. Теоремы о пределах. Замечательные пределы. Бесконечно малые функции
Теория пределов. Понятие предела. Предел функции в точке. Теоремы о пределах. Замечательные пределы. Бесконечно малые функции Трапеция
Трапеция pril
pril Проценты
Проценты Կրճատ բազմապատկման բանաձևեր
Կրճատ բազմապատկման բանաձևեր Золотое сечение
Золотое сечение