Площадь криволинейной трапеции и интеграл

Криволинейная трапеция
Отрезок [a;b] называют основанием
этой криволинейной трапеции
Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].

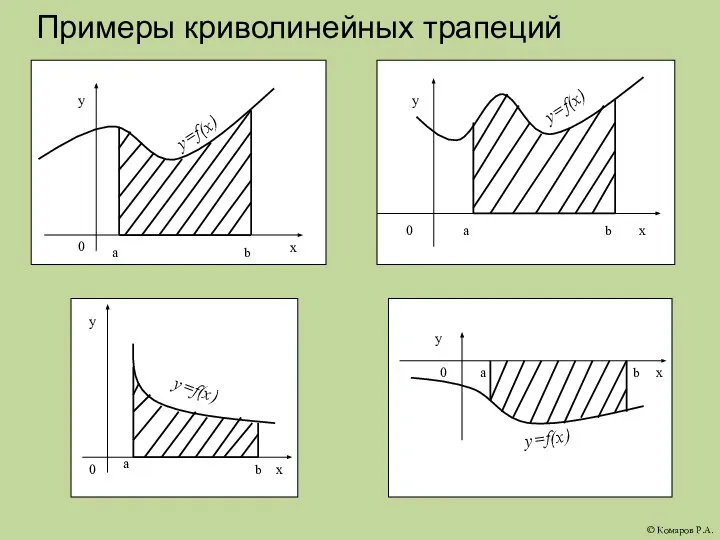
Примеры криволинейных трапеций
© Комаров Р.А.

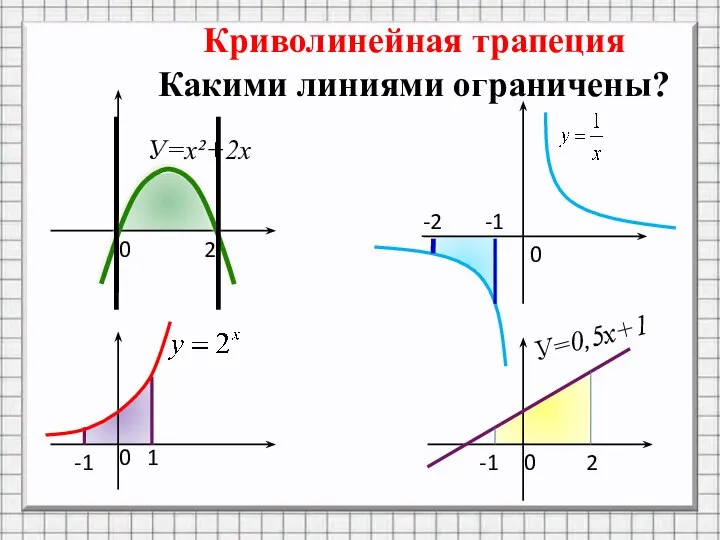
Криволинейная трапеция
Какими линиями ограничены?
0
2
0
0
0
1
-1
-1
2
-1
-2
У=х²+2х
У=0,5х+1

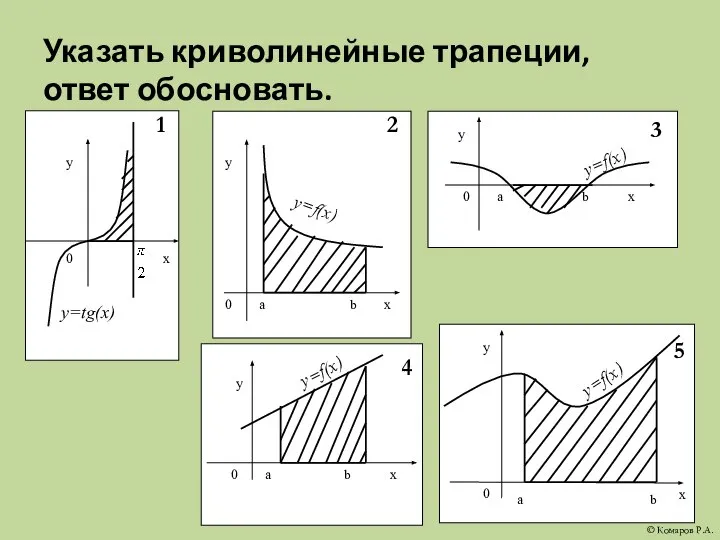
Указать криволинейные трапеции, ответ обосновать.
© Комаров Р.А.

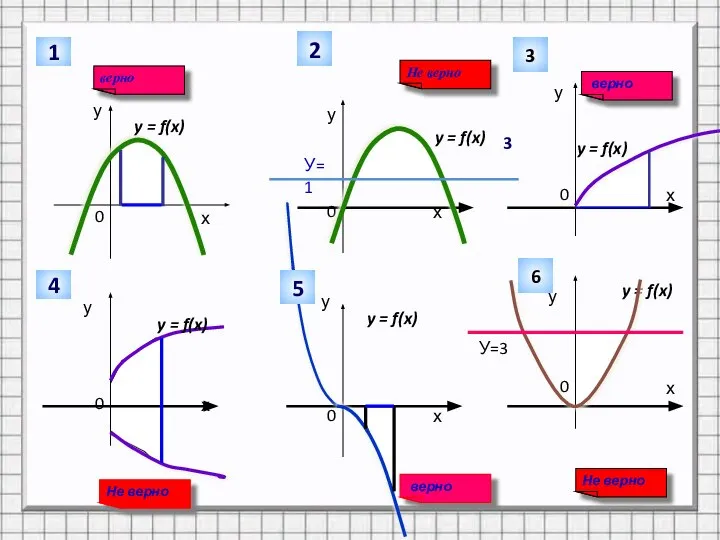
Какие из заштрихованных на рисунке фигур являются криволинейными трапециями, а какие нет?

у
1
Не верно
у
у
у
у
у
У=1
2
верно
3
3
y = f(x)
y = f(x)
y = f(x)
y = f(x)
y = f(x)
y = f(x)
У=3
4
5
6
Не верно
Не верно
верно
верно

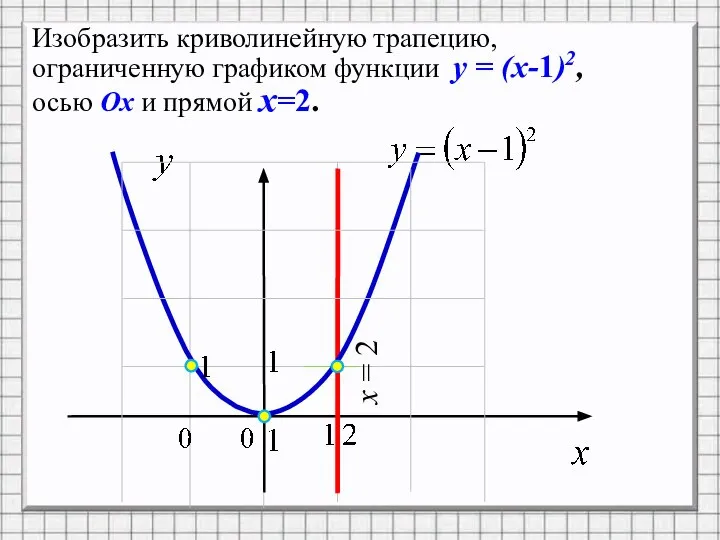
Изобразить криволинейную трапецию, ограниченную графиком функции y = (x-1)2, осью Ox и прямой x=2.
x = 2

Определённый интеграл

Задачи, приводящие к понятию определённого интеграла
Для функции y=f(x) на отрезке [a;b]:
Разбить отрезок [a;b] на n равных частей
Составить сумму Sn =f(x0)·∆x0+…+ f(xn)·∆xn
Вычислить предел этой суммы при n→∞

Понятие определённого интеграла
Предел такой суммы называют
определённым интегралом по отрезку [a;b]:
а – нижний предел
b – верхний предел

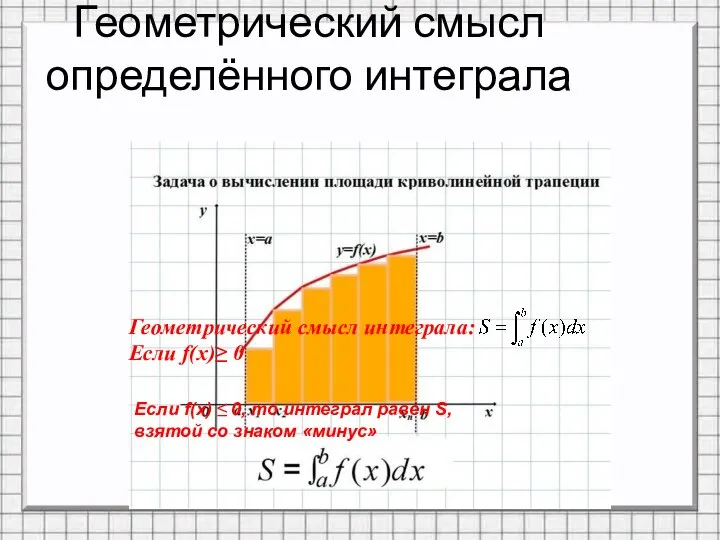
Геометрический смысл определённого интеграла
Если f(x) ≤ 0, то интеграл равен S, взятой со знаком «минус»

Формула Ньютона-Лейбница
Урок №2

Формула Ньютона-Лейбница

Формула Ньютона-Лейбница
Ньютон открыл новый метод раньше, но
опубликовал его позже Лейбница, написав ему:
«Надеюсь, что я при этом не написал ничего,
что было бы тебе неприятно, если же это
случилось, то прошу сообщить, потому что
друзья мне дороже математических открытий»
Лейбниц ответил в резкой форме. Распря двух
гениев дорого обошлась науке: английская
математическая школа увяла на целый век,
а европейская проигнорировала многие
выдающиеся идеи Ньютона.
Спор тянулся почти 40 лет, пока аббат Конти не
сообщил Ньютону: «Лейбниц умер – диспут окончен»

Вычисление определённого интеграла

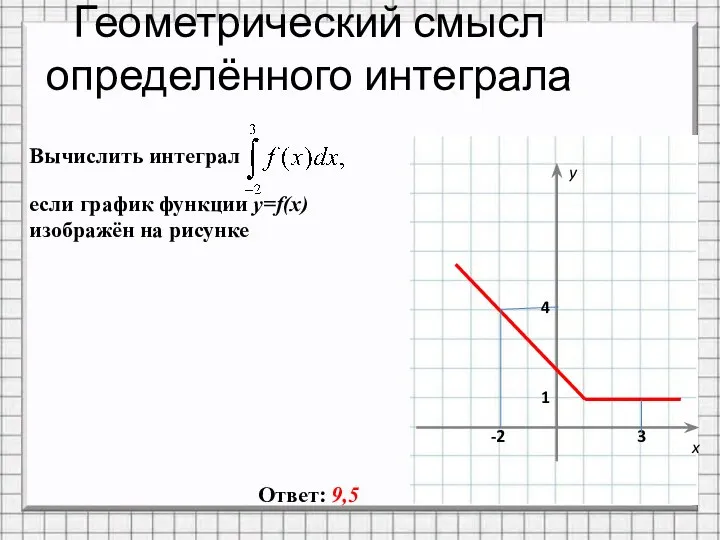
Геометрический смысл определённого интеграла
Ответ: 9,5

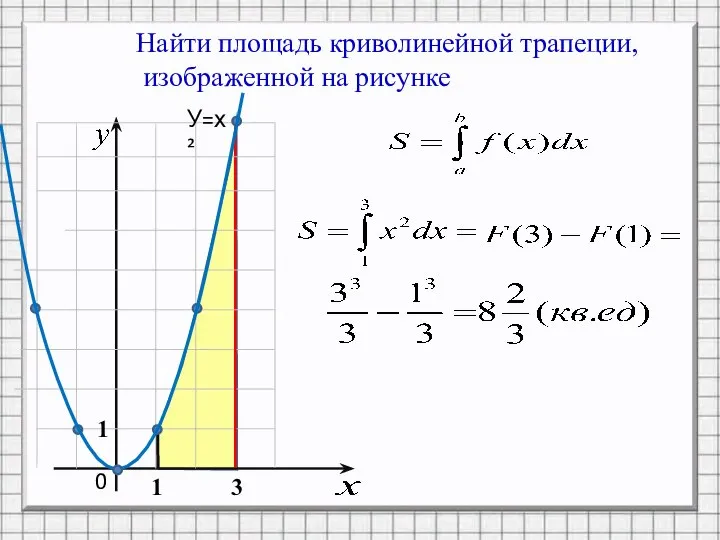
Найти площадь криволинейной трапеции,
изображенной на рисунке
0
1
3
У=х²
1