Содержание
- 2. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины , которое описывается плотностью: где – λ постоянная
- 3. Функция распределения показательного закона:
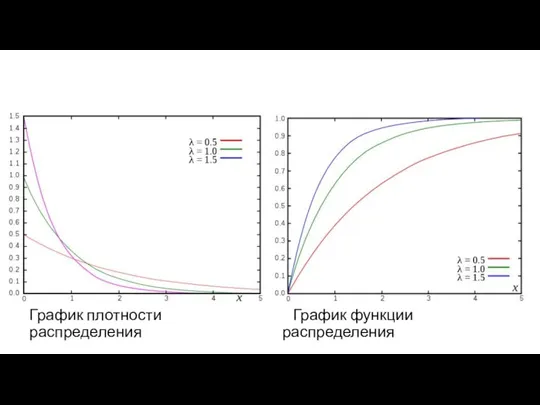
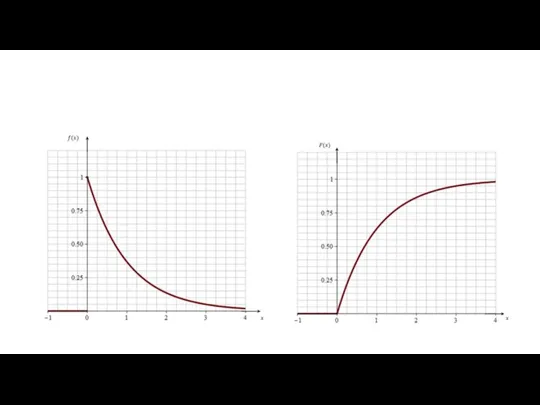
- 4. График плотности распределения График функции распределения
- 5. Вероятность попадания в интервал (a,b) непрерывной случайной величины X, распределенной по показательному закону:
- 6. Математическое ожидание случайной величины, распределенной по показательному закону:
- 7. Дисперсия случайной величины, распределенной по показательному закону
- 8. Среднее квадратическое отклонение случайной величины, распределенной по показательному закону:
- 9. Пример 1 Случайная величина ξ задана функцией распределения: Найдите математическое ожидание и среднее квадратическое отклонение этого
- 10. Решение Математическое ожидание случайной величины, распределенной по показательному закону: Среднее квадратическое отлонение: Вероятность того, что случайная
- 11. Пример 2 Постройте интегральную и дифференциальную функции распределения случайной величины X. Найдите математическое ожидание M(X), дисперсию
- 12. Решение Плотность распределения случайной величины X, распределенной по показательному закону: Функция распределения:
- 14. Математическое ожидание показательно распределенной случайной величины X: Дисперсия: Среднее квадратическое отклонение:
- 15. Пример 3 Длительность телефонного разговора подчиняется показательному закону. Найти среднюю длительность разговора, если вероятность того, что
- 16. Решение Используем известную формулу для показательного распределения: По условию, известна вероятность того, что того, что разговор
- 17. Пример 4 Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора
- 18. Решение Функция распределения имеет вид:
- 19. Найдем вероятность того, что в течение 100 часов прибор не выйдет из строя, то есть вероятность
- 21. Скачать презентацию
















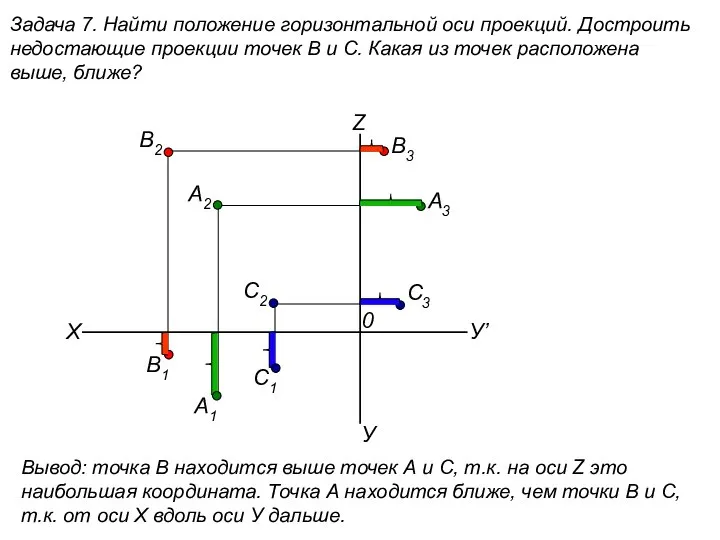 Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7)
Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7) LP (1)
LP (1)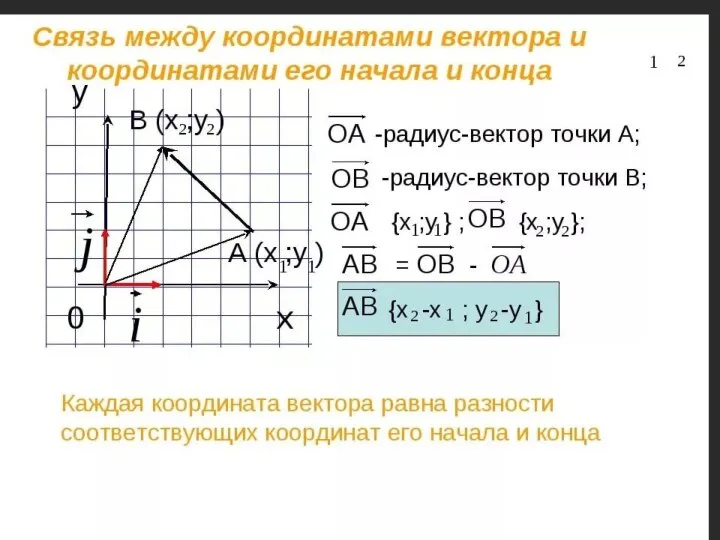 Векторы
Векторы Тест Проверь себя. ГИА (Четырёхугольники)
Тест Проверь себя. ГИА (Четырёхугольники) Решение задач. Урок №68
Решение задач. Урок №68 Геометрические места точек. (7 класс)
Геометрические места точек. (7 класс) Прямолинейный тренд
Прямолинейный тренд Применение основных тригонометрических формул к решению уравнений
Применение основных тригонометрических формул к решению уравнений Булева алгебра. Семинар №2
Булева алгебра. Семинар №2 Презентация на тему Нумерация многозначных чисел (4 класс)
Презентация на тему Нумерация многозначных чисел (4 класс)  Сложение чисел
Сложение чисел Решение задач по теме Арифметическая прогрессия
Решение задач по теме Арифметическая прогрессия Взаимное расположение прямой и окружности, двух окружностей
Взаимное расположение прямой и окружности, двух окружностей Блиц-турнир по математике
Блиц-турнир по математике Многогранники. Прямоугольные параллелепипеды
Многогранники. Прямоугольные параллелепипеды Элективный курс. Алгебра 11 класс. Уроки 10
Элективный курс. Алгебра 11 класс. Уроки 10 Тема: 14 -
Тема: 14 - Организация исследовательской деятельности учащихся по математике
Организация исследовательской деятельности учащихся по математике Геометрические фигуры (интерактивная игра)
Геометрические фигуры (интерактивная игра) Взаимное расположение прямой и окружности. Касательная
Взаимное расположение прямой и окружности. Касательная Решение составных задач
Решение составных задач Геометрия. 8 класс
Геометрия. 8 класс Простейшие задачи в координатах
Простейшие задачи в координатах Основное свойство арифметического квадратного корня
Основное свойство арифметического квадратного корня Действия над векторами в пространстве
Действия над векторами в пространстве Применение распределительного свойства умножения
Применение распределительного свойства умножения Тождественные преобразования. 7 класс
Тождественные преобразования. 7 класс Математическая карусель
Математическая карусель