Содержание
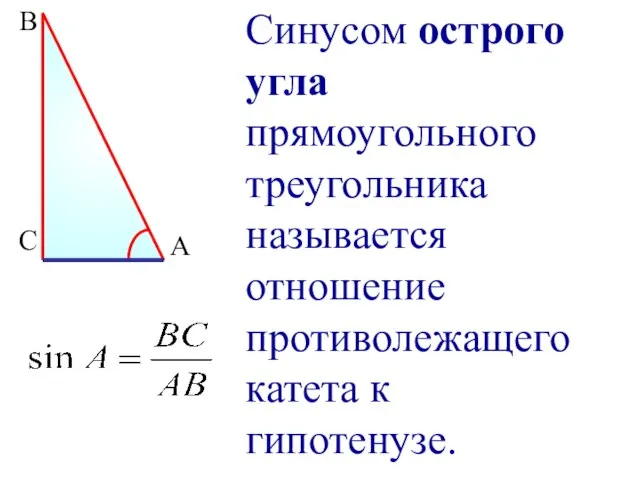
- 2. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. В С А
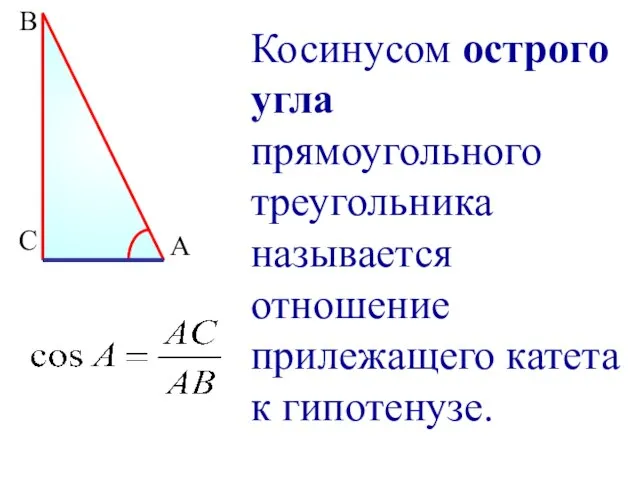
- 3. В С А Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
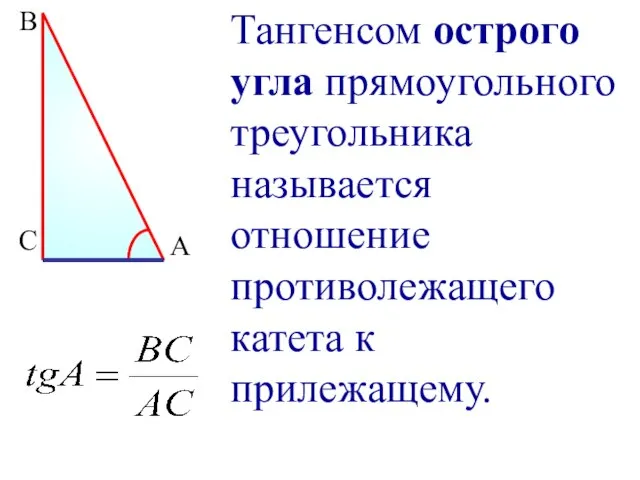
- 4. В С А Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
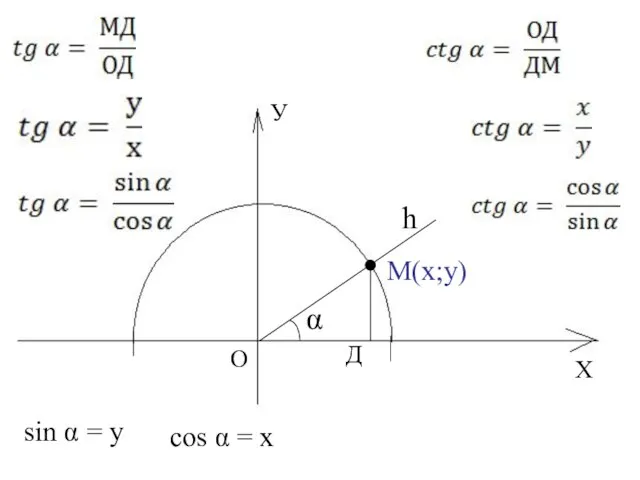
- 5. Х У О А(1;0) В(-1;0) С(0;1) Единичная полуокружность h М(х;у) α Д Рассмотрим ∆ОДМ ОМ=1, МД=
- 6. sinα-? cos α-? sin0°= 0 sin90°= 1 sin180°= 0 cos0°= 1 cos90°= 0 cos180°= -1 У
- 7. Х У О h М(х;у) α Д sin α = у cos α = х
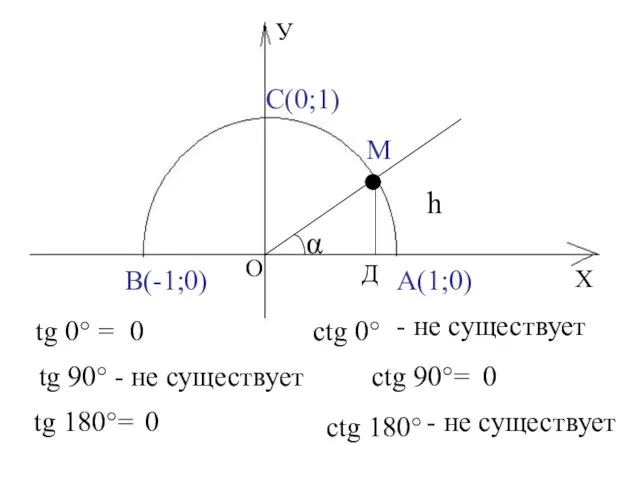
- 8. Х У О А(1;0) В(-1;0) С(0;1) h М α Д tg 0° = tg 90° 0
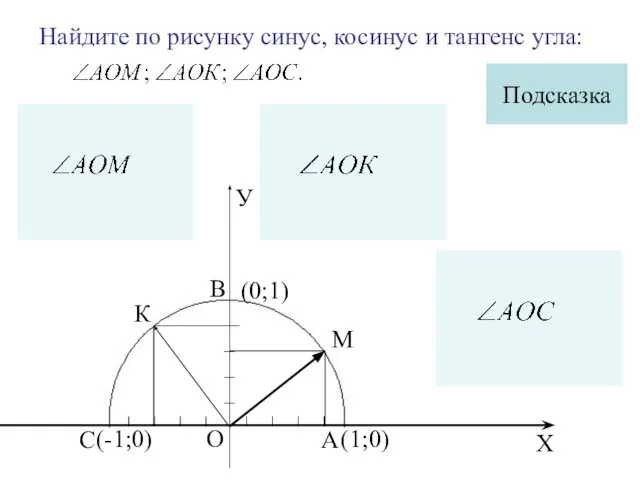
- 9. Найдите по рисунку синус, косинус и тангенс угла: К М А С Подсказка В
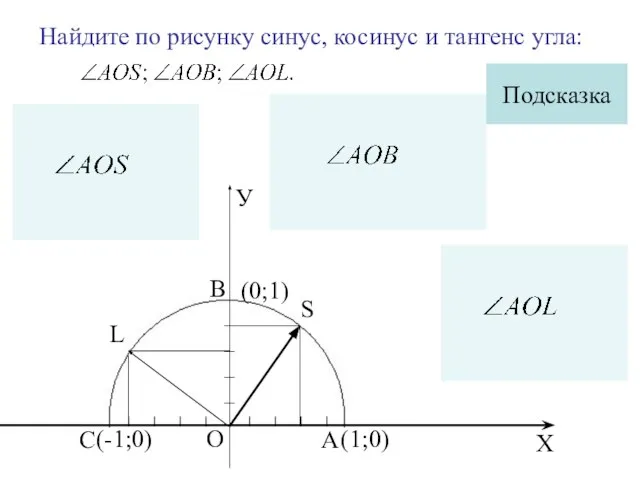
- 10. Найдите по рисунку синус, косинус и тангенс угла: L S А С Подсказка В
- 11. -уравнение окружности R=1, О(0;0) Основное тригонометрическое тождество М(х;у) x y
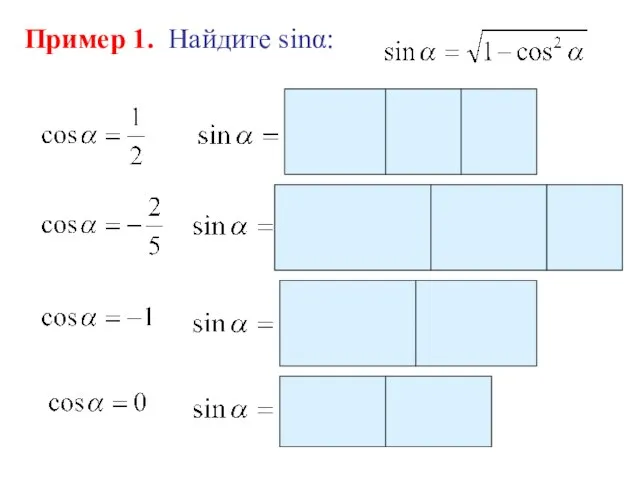
- 12. Пример 1. Найдите sinα:
- 13. Пример 2. Найдите cosα: ± ± ± ± ± ±
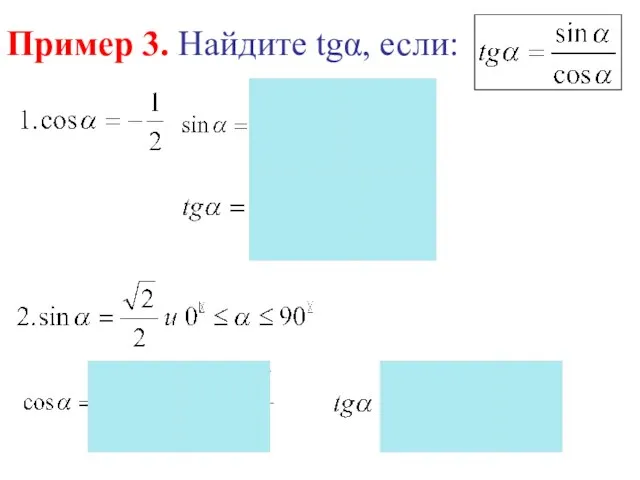
- 14. Пример 3. Найдите tgα, если:
- 15. Формулы приведения при 0° ≤ α ≤ 90° sin (90° - α) = cos α cos
- 17. Скачать презентацию





 Векторный анализ -теория поля. Типы векторных полей. Лекция 18
Векторный анализ -теория поля. Типы векторных полей. Лекция 18 Аналитическая геометрия в пространстве
Аналитическая геометрия в пространстве Дифференциальное исчисление для функции нескольких переменных. Метрические пространства
Дифференциальное исчисление для функции нескольких переменных. Метрические пространства Применение векторов к решению задач. 9 класс
Применение векторов к решению задач. 9 класс Уравнение
Уравнение Занимательная математика. 2 класс
Занимательная математика. 2 класс Математический диктант. Задачи. 1 класс
Математический диктант. Задачи. 1 класс Пространство IsR центрированных интервалов
Пространство IsR центрированных интервалов Симметрия. Виды симметрии
Симметрия. Виды симметрии Прибавить и вычесть 4
Прибавить и вычесть 4 Вывод формулы длины окружности и площади круга
Вывод формулы длины окружности и площади круга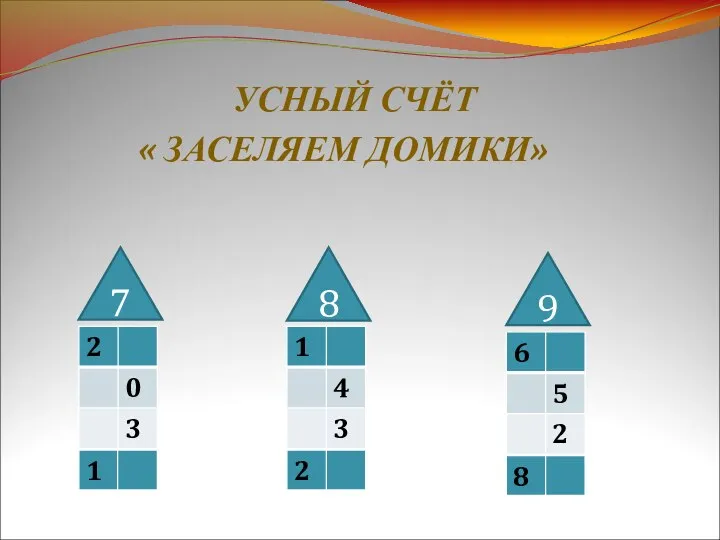 Усный счёт Заселяем домики
Усный счёт Заселяем домики Прямая, кривая, ломаная
Прямая, кривая, ломаная Решение задач. Продолжи ряд чисел
Решение задач. Продолжи ряд чисел Свойства арифметического корня
Свойства арифметического корня Основные принципы комбинаторики
Основные принципы комбинаторики Свойства сложения. 2 класс
Свойства сложения. 2 класс Презентация к уроку математики 6 класса учителя математики НОУ СОШ «Азъ Буки Веди» Ивахненко Натальи Геннадьевны
Презентация к уроку математики 6 класса учителя математики НОУ СОШ «Азъ Буки Веди» Ивахненко Натальи Геннадьевны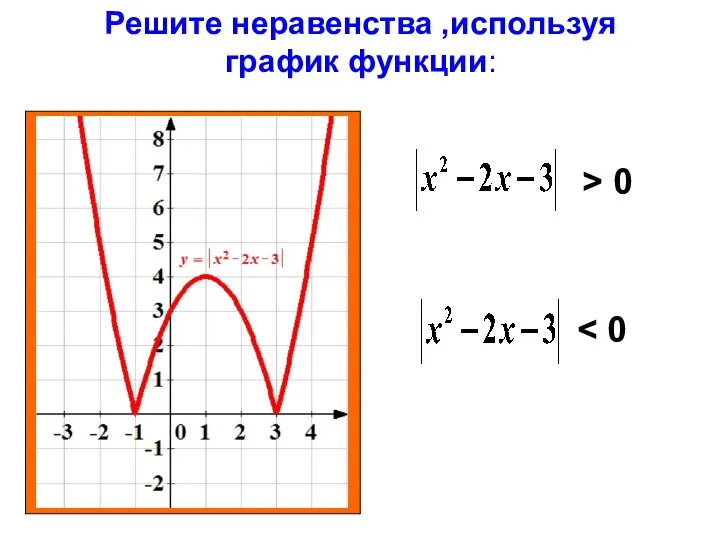 Решите неравенства ,используя график функции: x 2x 3 > 0
Решите неравенства ,используя график функции: x 2x 3 > 0 Нахождение числа по заданному значению его дроби
Нахождение числа по заданному значению его дроби Решение задач. Периметр и площадь
Решение задач. Периметр и площадь Уравнения высших степеней
Уравнения высших степеней арифметический корень (1)
арифметический корень (1) Правильные многогранники и ИДСЗ
Правильные многогранники и ИДСЗ Волшебная страна - Геометрия. Занятие 4
Волшебная страна - Геометрия. Занятие 4 Единицы времени. Час. минута
Единицы времени. Час. минута Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM
Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM Корни уравнения
Корни уравнения