Осевая симметрия

«Симметрия
является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство».
Герман Вейль

С симметрией мы часто встречаемся в искусстве, архитектуре, технике, быту. Так фасады многих зданий обладают осевой симметрией. В большин-стве случаев симметрич-ны относительно оси или центра узоры на коврах, тканях, комнатных обо-ях. Симметричны многие детали механизмов.

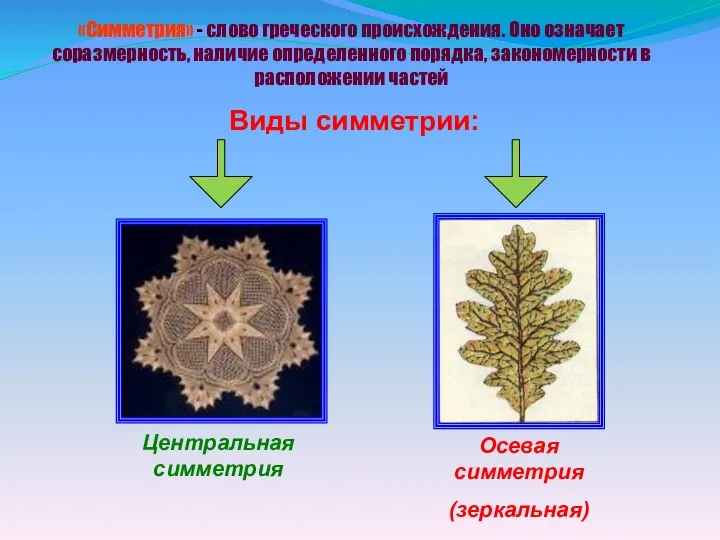
Виды симметрии:
Осевая симметрия
(зеркальная)
Центральная симметрия
«Симметрия» - слово греческого происхождения. Оно означает соразмерность, наличие определенного порядка, закономерности в расположении частей

Осевая симметрия
Фигура называется симмет-ричной относительно прямой a, если для каждой точки фигуры симметричная ей точка отно-сительно прямой a также при-надлежит этой фигуре. Прямая a называется осью симметрии фигуры.
Рассмотрите данные фигуры. Каждая из них состоит как бы из двух полови-нок, одна из ко-торых является зеркальным отра-жением другой. Каждую из этих фигур можно сог-нуть «пополам» так, что эти поло-винки совпадут. Говорят, что эти фигуры симмет-ричны относи-тельно прямой – линии сгиба.

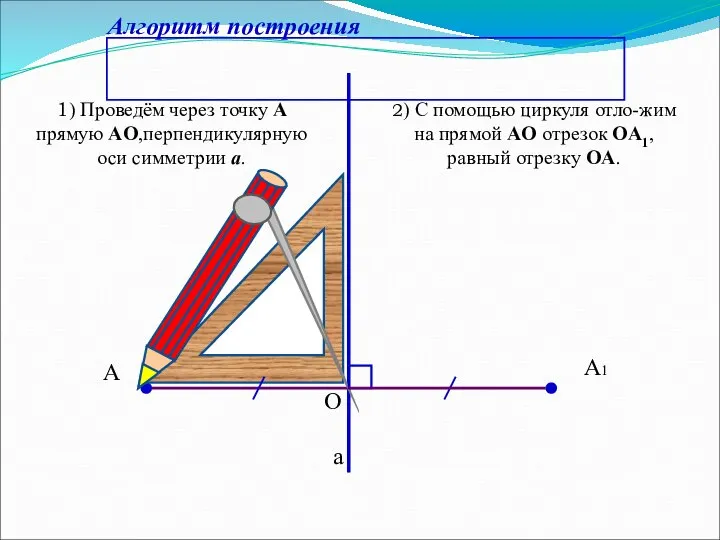
Алгоритм построения
А
А1
а
1) Проведём через точку А прямую АO,перпендикулярную оси симметрии a.
2) С помощью циркуля отло-жим на прямой АO отрезок OА1, равный отрезку OА.
О

Точки А и А1 называются симметричными относительно прямой а, если:
эта прямая проходит через середину отрезка АА1,
а перпендикулярна АА1 .
А
А1
а
a – ось симметрии.
Точка А симметрична точке А1 относительно прямой а.
О

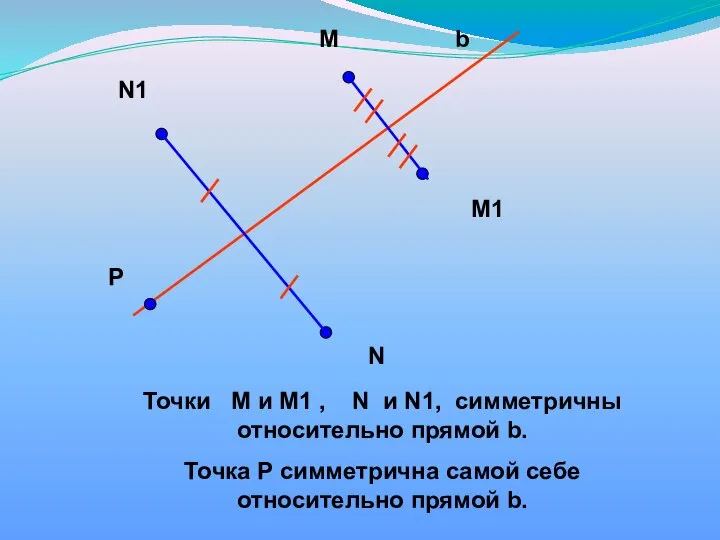
М
М1
N1
N
P
b
Точки М и М1 , N и N1, симметричны относительно прямой b.
Точка P симметрична самой себе относительно прямой b.

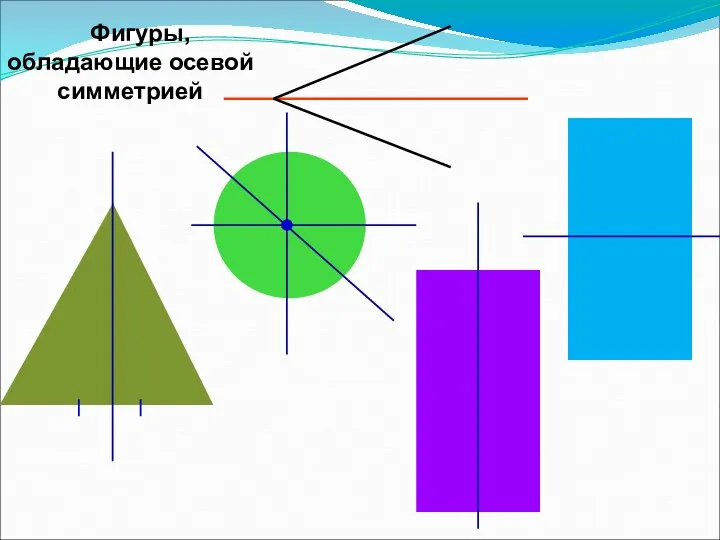
Фигуры, обладающие осевой симметрией

Прямоугольник имеет две оси симметрии

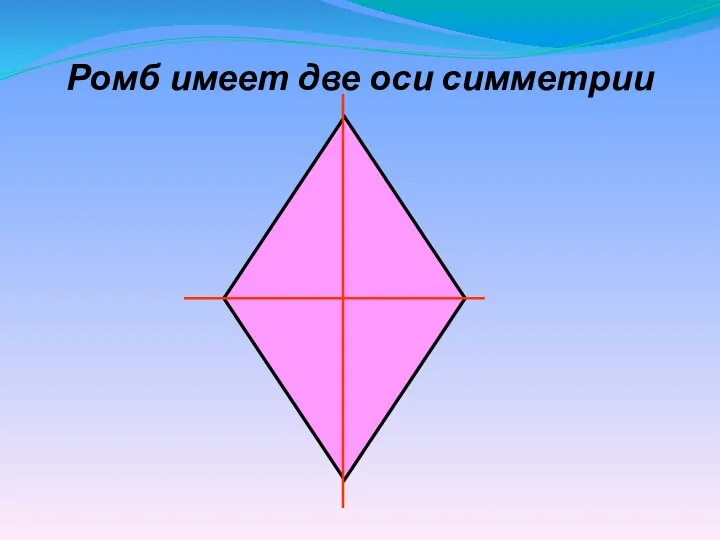
Ромб имеет две оси симметрии

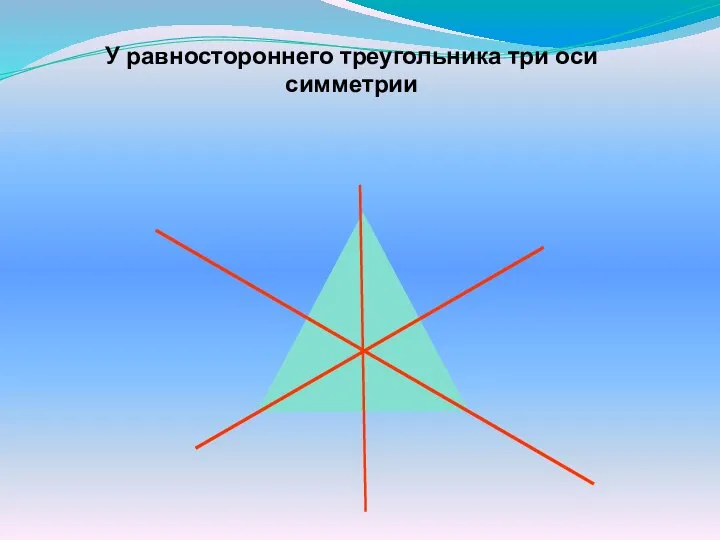
У равностороннего треугольника три оси симметрии

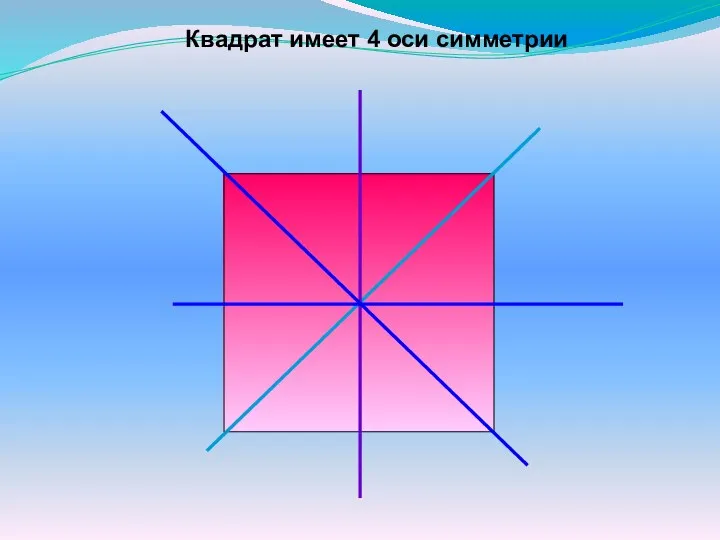
Квадрат имеет 4 оси симметрии

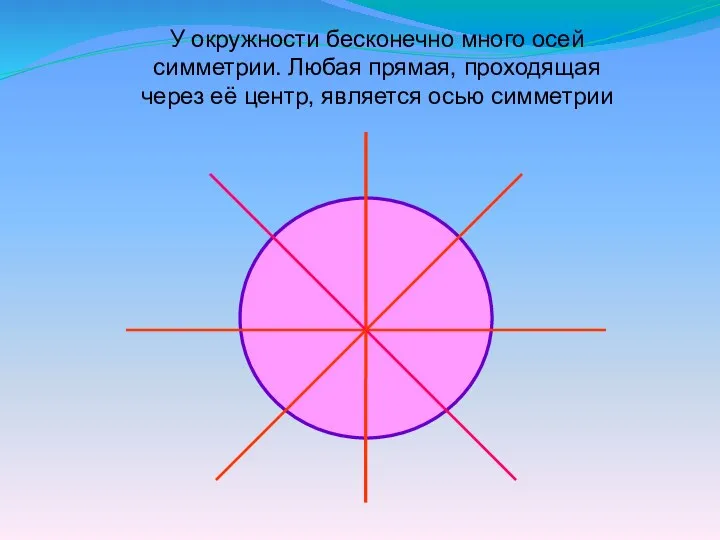
У окружности бесконечно много осей симметрии. Любая прямая, проходящая через её центр, является осью симметрии

Ось симметрии имеют плоские и пространственные фигуры.
Например:
Задание.
Из данных фигур выберите те, которые имеют ось симметрии. Есть ли среди них такие, которые имеют более одной оси симметрии?

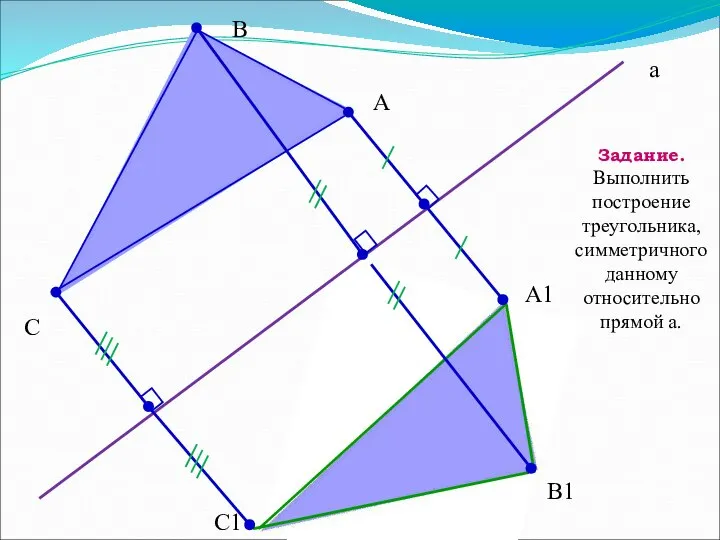
B
C
А
C1
B1
A1
а
Задание. Выполнить построение треугольника, симметричного данному относительно прямой a.

Осевая симметрия в животном мире

Кто из нас зимой не любовался снежинками? Форма снежинок может быть очень разнообразной, но все они обладают симметрией
Симметрия везде

В классе:
№6 стр.50,
16 стр 53,
18 стр 53