Слайд 5Решение: Сначала узнаем скорость движения катера против течения реки, для этого от

его собственной скорости отнимем скорость течения:
30 - 2 = 28 (км/ч) – скорость движения катера против течения.
Теперь можно узнать за сколько часов катер преодолеет 112 км, разделив расстояние на скорость:
112 : 28 = 4 (ч)
Слайд 6Реши задачу: Найди высоту прямоугольного параллелепипеда, если длины сторон прямоугольника в основании

равны 3м и 6м, а объём геометрического тела равен 90м3 .
Слайд 7V = a·b·h
V — это объём, a — длина, b —

ширина, h — высота
Нам известен объём, длина и ширина
Найдём высоту:
h = V ÷ (a·b)
h = 90 ÷ (3·6) = 90:(3·6) = 30:6 = 5 м
Ответ: высота равна 5 метров
Слайд 8Реши задачу: Катер движется против течения реки. За сколько часов он преодолеет

расстояние 112 км, если его собственная скорость 30 км/ч, а скорость течения реки 2 км/ч?
Слайд 9Решение: Сначала узнаем скорость движения катера против течения реки, для этого от

его собственной скорости отнимем скорость течения:
30 - 2 = 28 (км/ч) – скорость движения катера против течения.
Слайд 10Теперь можно узнать за сколько часов катер преодолеет 112 км, разделив расстояние

на скорость:
112 : 28 = 4 (ч)
Слайд 11Решение задачи по действиям можно записать так:
1) 30 - 2 = 28

(км/ч) – скорость движения катера против течения
2) 112 : 28 = 4 (ч)
Ответ: За 4 часа катер преодолеет расстояние 112 км.
Слайд 12Примеры уравнений на сложение.
15 + x = 32
у + 10 = 14
27

+ 12 = z
Слайд 13Примеры уравнения на вычитание.
38 - x = 23
у - 16 = 19
29

- 14 = z
Слайд 14Примеры уравнений на умножение и деление.
28 * x = 56
у : 10

= 3
27 * 4 = z
Слайд 1528 + (45 + х) = 100;
(у - 25) + 18 =
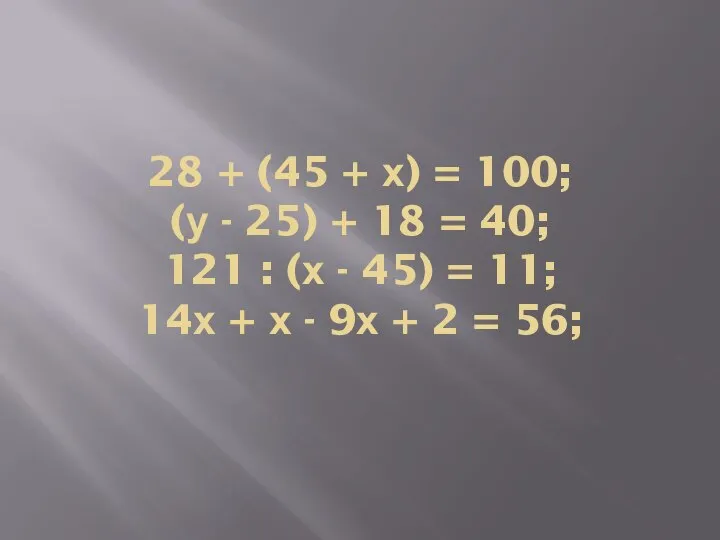
40;
121 : (х - 45) = 11;
14х + х - 9х + 2 = 56;
Слайд 16Реши задачу с помощью уравнения: Лена загадала некоторое число. Если это число

уменьшить на 12, то получится 5. Какое число загадала Лена
Слайд 17Реши задачу с помощью уравнения:
Сколько лет маме, если она старше дочери на

24 года, а дочь моложе матери в 7 раз?













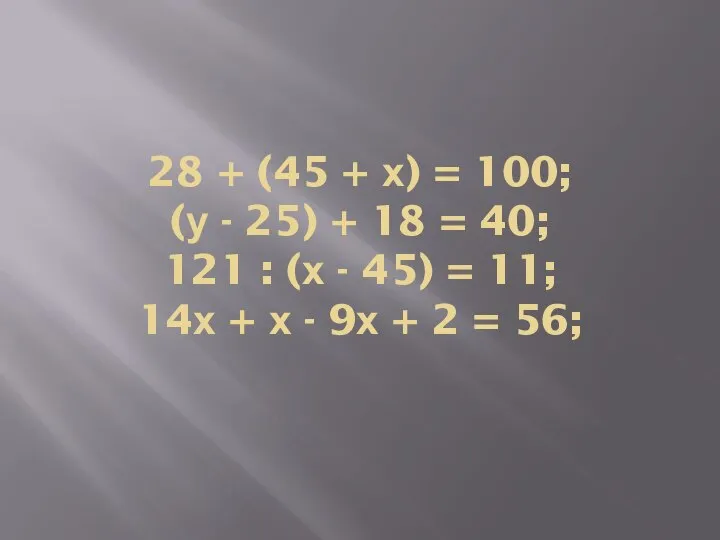


 Симметрия в пространстве
Симметрия в пространстве Оптимизация по методу Бокса-Уилсона
Оптимизация по методу Бокса-Уилсона Прямоугольник. Теоремы
Прямоугольник. Теоремы Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Умножение десятичной дроби на единицу с нулями
Умножение десятичной дроби на единицу с нулями Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Вписанная окружность
Вписанная окружность Многогранники. Стереометрия
Многогранники. Стереометрия Правильный многоугольник
Правильный многоугольник Окружность и круг
Окружность и круг Умножение на 2. Проведите динозаврика по лабиринту (2)
Умножение на 2. Проведите динозаврика по лабиринту (2) Задачи на умножение
Задачи на умножение Случайные величины
Случайные величины Равенство векторов
Равенство векторов Графы
Графы Экономический факторный анализ. Теорема о среднем
Экономический факторный анализ. Теорема о среднем Счет до 10
Счет до 10 Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного
Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного Упражнения
Упражнения Состав чисел в приделах 10. Закрепление изученного материала
Состав чисел в приделах 10. Закрепление изученного материала Решение задач на нахождение зависимости между величинами используя графики
Решение задач на нахождение зависимости между величинами используя графики График функции
График функции Математический диктант
Математический диктант Применение векторов к решению задач (9 класс)
Применение векторов к решению задач (9 класс) Метод рационализации в логарифмических неравенствах
Метод рационализации в логарифмических неравенствах Numbers and animals
Numbers and animals Свойства функций
Свойства функций Умножение обыкновенных дробей
Умножение обыкновенных дробей