Признак параллельности прямых по равенству соответственных углов

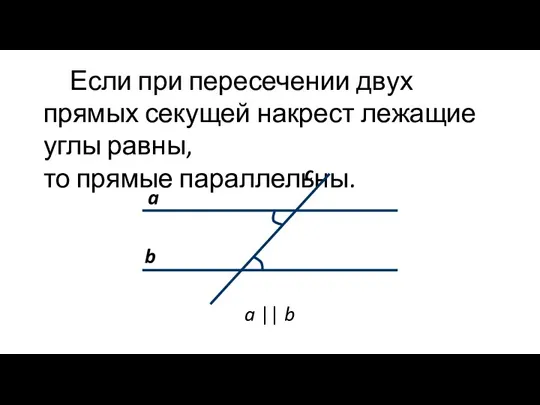
Если при пересечении двух прямых секущей накрест лежащие углы равны,
то прямые параллельны.
a
b
c
a || b

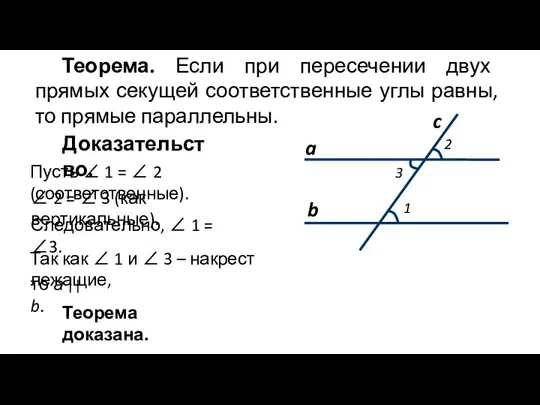
Теорема. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Доказательство.
Следовательно, ∠ 1 = ∠3.
Так как ∠ 1 и ∠ 3 – накрест лежащие,
то а || b.
Теорема доказана.

Задача. Прямая а параллельна прямой b. Прямая c – секущая при этих параллельных прямых. Найдите все углы равные углу 1.
Решение.
1
2
3
4
5
6
7
8
a
b
c
∠ 1 = ∠ 5 (как соответственные),
∠ 1 = ∠ 3 (как вертикальные),
∠ 5 = ∠ 7 (как вертикальные),
следовательно, ∠ 1 = ∠ 7.
Ответ: ∠ 3, ∠ 5, ∠ 7.

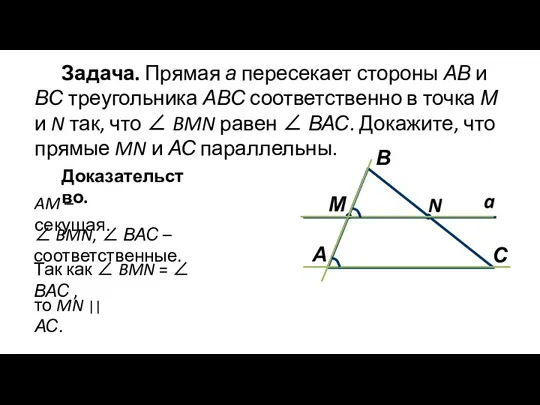
Задача. Прямая а пересекает стороны АВ и ВС треугольника АВС соответственно в точка М и N так, что ∠ BMN равен ∠ ВАС. Докажите, что прямые MN и АС параллельны.
Доказательство.
А
N
М
С
В
a
AM – секущая.
∠ BMN, ∠ ВАС – соответственные.
Так как ∠ BMN = ∠ ВАС ,
то MN || АС.