Определение производной. Правила вычисления производных. Таблица производных

Урок 54.
Тема: Определение производной. Правила вычисления производных. Таблица производных

Цели обучения:
10.3.1.9 - знать определение производной функции и находить производную функции по определению;
10.3.1.10 - находить производные постоянной функции и степенной функции;
10.3.1.11 - знать и применять правила дифференцирования

у=f(х)
Пусть дана функция у=f(х)
y
x
0
х
х0
Пусть х – произвольная точка в окрестности
фиксированной точки х0
Разность х-х0 называется
приращением аргумента и обозначается
Разность f(x)-f(x0) называется приращением функции
и обозначается
∆f = f(x)-f(x0) или
∆f =f(x0+ ∆x)-f(x0) - приращение функции
∆х=х- х0 – приращение аргумента
∆ x =x-x0 х=х0+ ∆ x
Изучение нового материала

Определение производной
Если разностное отношение имеет предел при то его называют производной функции в т.
Вообще данную операцию называют дифференцированием функции, а производная – это результат дифференцирования

Пример: и найти
т.е. - производная функции
- производная функции в т.

Схема вычисления производной функции:
1. Найти приращение функции на отрезке [ x; x+Δx]:
2. Разделить приращение функции на приращение аргумента:
3. Найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Задание: Найти производную функции:
1.
2.
3.
4.
5.

Решение 1: Вычислить производную функции
1.
2.
3.

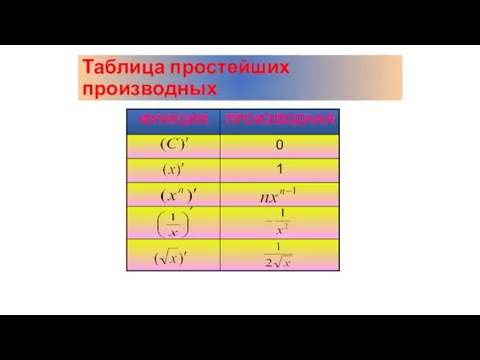
Таблица простейших производных

Правила дифференцирования (вычисления производных)
(1)
(2)
(3)
Следствия:

Примеры.
1)
2)
3)
4)