Погрешность измерения

Погрешность измерения
Погрешность результата измерения – разность между измеренным значением величины и опорным значением величины.
X – измеренное значение величины,
xоп – опорное значение величины,
Δ – погрешность.
В качестве опорного может выступать истинное значение измеряемой величины.

Погрешность измерения
Истинное значение величины xи идеальным образом отражает свойства данного объекта в количественном и качественном отношении.
На практике истинное значение величины определить невозможно, поэтому значение погрешности остается неизвестным.

Погрешность измерения
Действительное значение величины xд может быть найдено экспериментальным путем. Оно настолько близко к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
После замены истинного значения величины на действительное становится возможным нахождение значения погрешности.

Классификация погрешностей
в зависимости от места возникновения
1) Инструментальная (аппаратурная) погрешность – составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений.
К инструментальным погрешностям относятся:
- погрешность схемы,
- технологическая погрешность.
2) Методическая (теоретическая) погрешность – составляющая погрешности измерения, обусловленная несовершенством принятого метода измерений.
К методическим погрешностям относится:
- погрешность, связанная с несовершенством модели объекта.
3) Субъективная (личная) погрешность – составляющая погрешности измерения, обусловленная погрешностью отсчёта оператором по шкале средства измерений.

Классификация погрешностей
по способу математического выражения
1) Абсолютная погрешность – погрешность измерения, выраженная в единицах измеряемой величины.
2) Относительная погрешность – погрешность измерения, выраженная отношением абсолютной погрешности измерения к опорному значению (может заменятся на измеренное значение) измеряемой величины.

Классификация погрешностей
по характеру проявления
1) Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины.
В зависимости от характера изменения во времени систематические погрешности подразделяют на:
а) Постоянная погрешность – погрешность, которая в течение длительного времени (например, в течение времени выполнения всего ряда измерений) остается постоянной.
б) Прогрессирующая погрешность – погрешность, непрерывно возрастающая или убывающая.
в) Периодическая погрешность – погрешность, значение которой является периодической функцией времени.
г) Погрешность, изменяющаяся по сложному закону – погрешность, возникающая вследствие совместного действия нескольких систематических погрешностей.

Классификация погрешностей
по характеру проявления
2) Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных в определенных условиях.
Источником случайных погрешностей являются факторы, неожиданно появляющиеся и исчезающие с интенсивностью, которую сложно предвидеть.
3) Грубая погрешность – погрешность отдельного результата измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.

Математическая модель
погрешности измерения
В общем случае погрешность измерения рассматривается как случайная функция времени.
- постоянная или инфранизкочастотная нестационарная случайная функция, период изменения которой значительно больше времени проведения измерений,
- случайная составляющая, период изменения которой меньше или сравним со временем измерения:
- низкочастотная стационарная случайная функция, корреляционная функция которой затухает до нуля в течение времени, больше времени отдельного измерения,
- высокочастотная случайная составляющая, корреляционная функция которой затухает в течение времени, значительно меньше времени отдельного измерения,
- центрированная случайная величина, не зависящая от времени.

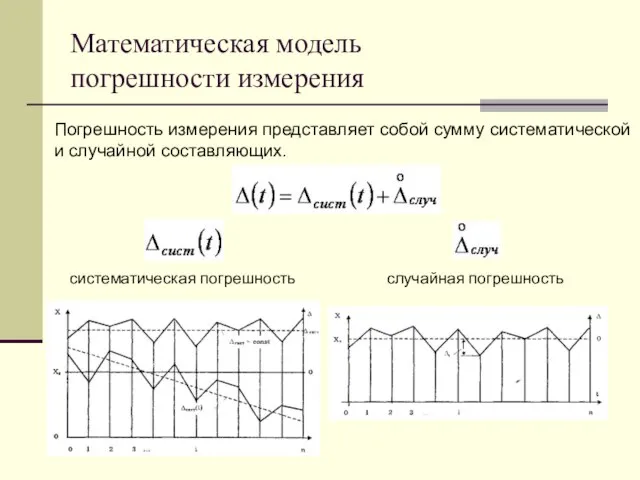
Математическая модель
погрешности измерения
Погрешность измерения представляет собой сумму систематической и случайной составляющих.
систематическая погрешность
случайная погрешность

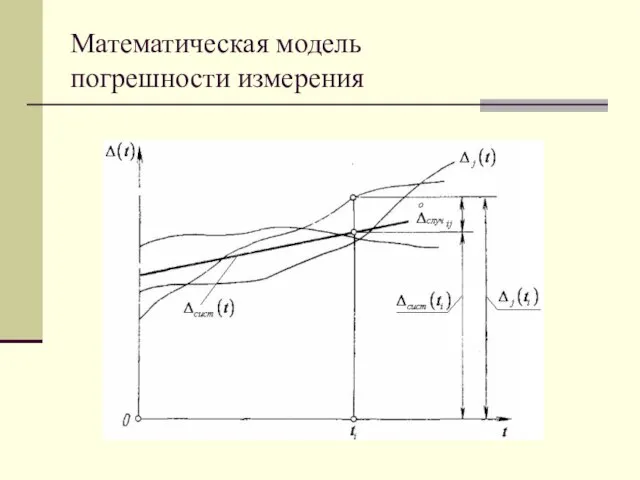
Математическая модель
погрешности измерения

Систематическая и случайная составляющие погрешности измерения
Из-за отличия свойств систематической и случайной погрешностей отличаются способы их обнаружения и уменьшения их воздействия на результат измерения.
Систематическая погрешность
Изменяющуюся во времени систематическую погрешность можно обнаружить путем обработки результатов многократных измерений.
Постоянную систематическую погрешность невозможно обнаружить, используя только результаты многократных измерений. Для этого проводят дополнительные исследования, измерения и расчеты.
При наличии информации о значении систематической погрешности становится возможным введение поправки, т.е. исключение ее из результатов измерений.
Полное исключение систематической погрешности из результатов измерений невозможно из-за отсутствия абсолютно точной информации о ее значении.

Систематическая и случайная составляющие погрешности измерения
Случайная погрешность
Случайную погрешность невозможно исключить из результатов измерений путем введения поправки.
Причина заключается в случайном (по знаку и значению) изменении случайной погрешности от измерения к измерению.
Влияние случайной погрешности на окончательный результат измерения можно существенно уменьшить путем проведения многократных измерений с последующей математической обработкой.
В качестве измеренного значения величины используют среднее арифметическое результатов многократных измерений.
При усреднении происходит взаимное «погашение» положительных и отрицательных случайных погрешностей, поэтому рассеяние среднего арифметического меньше рассеяния результата однократного измерения.

Распределение погрешности измерения
Пусть систематическая составляющая погрешности и распределение случайной составляющей погрешности не меняются.
Тогда погрешность измерения из случайной функции Δ(t) становится случайной величиной Δ.
Распределение погрешности Δ представляет собой смещенное на значение систематической погрешности распределение случайной погрешности.

Распределение результата измерения
Пусть измеряемая величина постоянна (xи – истинное значение измеряемой величины).
Тогда результат измерения X представляет собой случайную величину.
Распределение результата измерения X представляет собой смещенное на значение xи распределение погрешности измерения Δ.