Содержание
- 2. Формальная логика изучает только истинность и ложность высказываний. Логическое высказывание – это повествовательное предложение, относительно которого
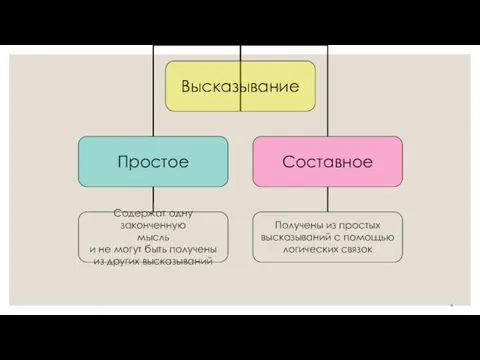
- 3. Высказыванием называется утверждение, которое является истинным или ложным
- 5. Основные логические операции Дизъюнкция – переход к составному высказыванию, которое является истинным, если истинно хотя бы
- 6. Основные логические операции Конъюнкция – переход к составному высказыванию, которое является ложным, если ложно хотя бы
- 7. Основные логические операции Отрицание (инверсия) – переход к новому высказыванию, которое является истинным, если высказывание А
- 8. Основные логические операции Импликация – переход к составному высказыванию, которое является ложным, если из истинного высказывания
- 9. Основные логические операции Эквиваленция – переход к составному высказыванию, которое является ложным, если посылки имеют противоположные
- 10. Другие логические операции Кольцевая сумма, сумма Жегалкина, сумма по модулю 2, двоичное сложение – антиэквиваленция Обозначение
- 11. Другие логические операции Стрелка Пирса – антидизъюнкция Обозначение Лексический аналог – «ни…, ни…» Стрелка Пирса истинна
- 12. Другие логические операции Штрих Шеффера – антиконъюнкция Обозначение Лексический аналог – «не… или не…» Штрих Шеффера
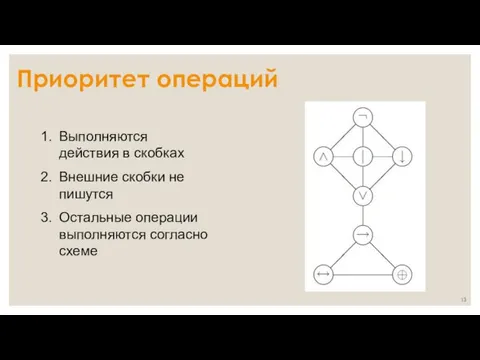
- 13. Приоритет операций Выполняются действия в скобках Внешние скобки не пишутся Остальные операции выполняются согласно схеме
- 14. Пример 2 3 4 1 5 6 1 2 3 4 5 6
- 15. Виды формул Формула называется тавтологией, если она принимает только истинные значения при любых значениях букв. Другими
- 16. Построение таблицы истинности Подсчитать количество переменных в формуле n. Определить количество строк в таблице – Подсчитать
- 17. Примеры n=3 m=6
- 18. Примеры n=3 m=6
- 20. Скачать презентацию















 Интерактивный тренажёр Счет в пределах 15
Интерактивный тренажёр Счет в пределах 15 Математические методы в филологии
Математические методы в филологии Построение сечения
Построение сечения Окружность и её элементы
Окружность и её элементы Универсальный тренажёр. Математика 2 класс
Универсальный тренажёр. Математика 2 класс Презентация на тему Круговые диаграммы (6 класс)
Презентация на тему Круговые диаграммы (6 класс)  Числовые домики. Тренажер
Числовые домики. Тренажер Задачи на готовых чертежах. Первый признак равенства треугольников. Устный счёт
Задачи на готовых чертежах. Первый признак равенства треугольников. Устный счёт Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Логические задачи. Мастер-класс
Логические задачи. Мастер-класс Метрологические аспекты спектрометрических и радиометрических измерений
Метрологические аспекты спектрометрических и радиометрических измерений Вопросы при решении задач
Вопросы при решении задач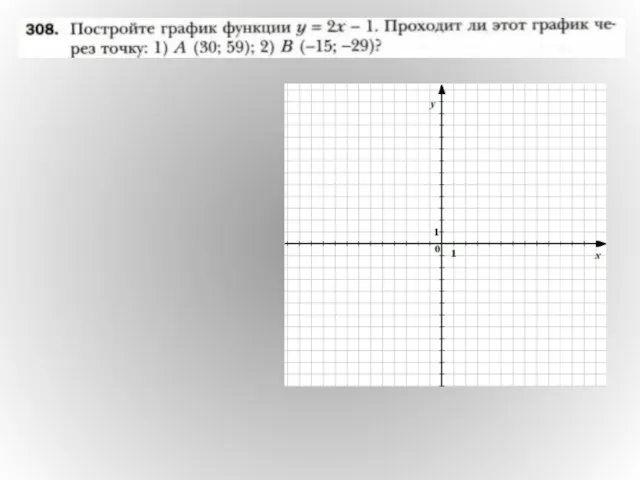 Функция y = k/х и её график
Функция y = k/х и её график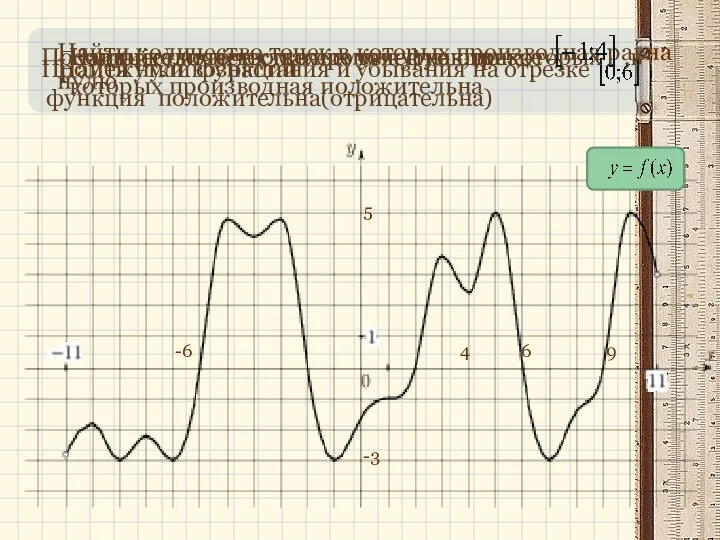 Алгоритм нахождения интервалов выпуклости и точек перегиба
Алгоритм нахождения интервалов выпуклости и точек перегиба Векторы в пространстве. Задачи
Векторы в пространстве. Задачи Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс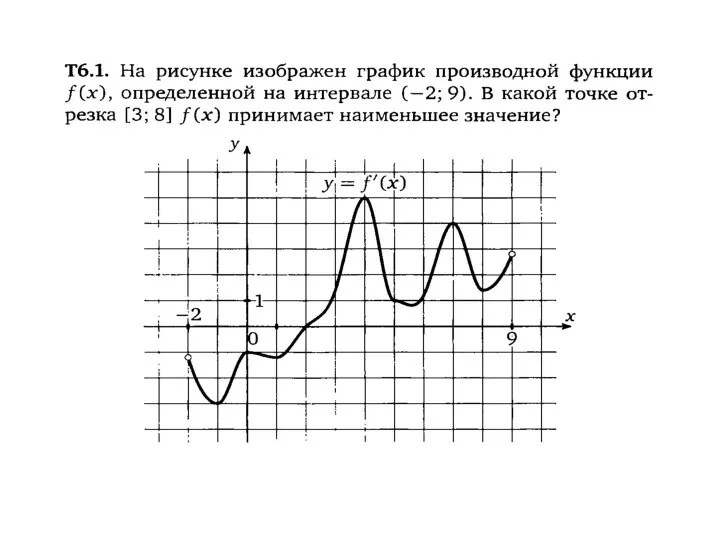 График производной функции
График производной функции Решение задач на работу
Решение задач на работу Письменное умножение и деление
Письменное умножение и деление Реляционная алгебра
Реляционная алгебра Комплeксные числа. Арифметические операции над ними (10 класс)
Комплeксные числа. Арифметические операции над ними (10 класс) Повторение. Дроби
Повторение. Дроби Прямо-пропорциональные величины
Прямо-пропорциональные величины Числовая последовательность
Числовая последовательность Решение неравеснств
Решение неравеснств Решение задач на движение. 8 класс
Решение задач на движение. 8 класс Lek-AFK-Differentsialnye_uravnenia
Lek-AFK-Differentsialnye_uravnenia Линейная функция. Блиц-опрос
Линейная функция. Блиц-опрос