Математический расчет или интуиция, что надежней?

Введение
Многие люди доверяют своему шестом чувству или наитию. Наша интуиция помогает нам в жизни. Чаще всего мы пользуемся ей в тот момент, когда других логических решений мы не видим. Как часто вы отвечали наугад? Как часто вы оказывались правы, как часто ошибались? Ну а что, если подойти к этим вопросам с точки зрения математики ?
Можно ли предсказать вероятность выигрыша или проигрыша использую логику и математический подсчет? Или надежней следовать своей интуиции? Математический расчет или интуиция, что надежней? Разобраться в этом мы можем на примере парадокса Монти Холла.

Парадокс Монти Холла
Парадокс Монти Холла - задача теории вероятности, вызвавшая многочисленные споры и дискуссии в научном мире. Решение этой задачи поначалу кажется нелогичным и странным, но если разобраться, то все становиться очевидно и понятно.
Содержание задачи - описание американского телешоу "Let's Make a Deal". Ведущим этой передачи был Монти Холл, собственно в честь него и назван парадокс.

Содержание задачи
"Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас — не желаете ли вы изменить свой выбор и выбрать дверь номер 2? Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?"

Решение парадокса Монти Холла с помощью разбития дверей на множества
Представим, что вы попали на телешоу "Let's Make a Deal", вас уже ознакомили с условиями игры и вот настало ваше время делать выбор. Вам более всего приглянулась дверь №1, вы выбираете ее, и ведущий, согласно условиям игры, открывает дверь , за которой находится коза, пусть это будет дверь №2, тогда перед вами остается две двери, дверь №1, та, что вы выбрали и дверь № 3 , та, что оставил закрытой ведущий. Вам задается долгожданный вопрос " Вы желаете остаться при своем выборе или измените его? ". Вот тут и начинается сама суть парадокса Монти Холла. Как я уже сказала ранее, большинство людей полагает, что теперь вероятность выигрыша составляет 50/50 %.

Но посмотрим с самого начла.
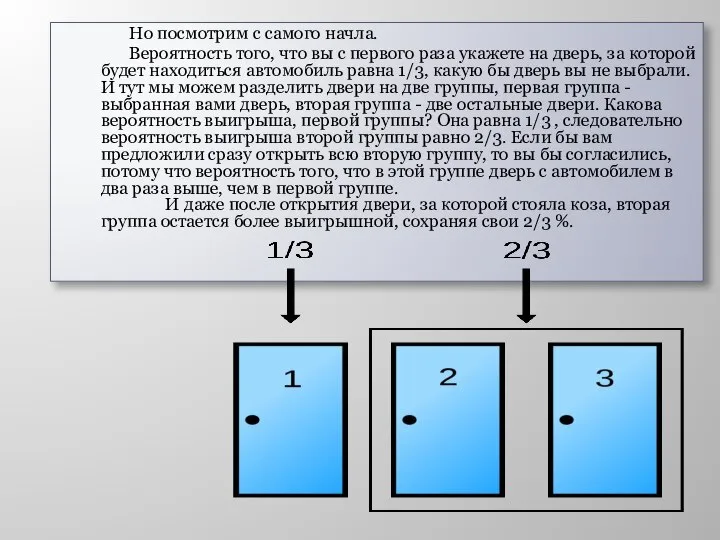
Вероятность того, что вы с первого раза укажете на дверь, за которой будет находиться автомобиль равна 1/3, какую бы дверь вы не выбрали. И тут мы можем разделить двери на две группы, первая группа - выбранная вами дверь, вторая группа - две остальные двери. Какова вероятность выигрыша, первой группы? Она равна 1/3 , следовательно вероятность выигрыша второй группы равно 2/3. Если бы вам предложили сразу открыть всю вторую группу, то вы бы согласились, потому что вероятность того, что в этой группе дверь с автомобилем в два раза выше, чем в первой группе.
И даже после открытия двери, за которой стояла коза, вторая группа остается более выигрышной, сохраняя свои 2/3 %.

Решение парадокса Монти Холла с помощью увеличения количества дверей
Рассмотрим случай, когда перед человеком находится не три двери, а предположим 50. Условия остаются те же самые - только за одной из дверей приз и ведущий обязан открыть все двери, кроме двух.
Теперь логичность смены решения становиться очевидной, потому что вероятность того, что вы с первого раза из 50 дверей выберете ту самую равна 1/50. Если вернуться к способу разделения дверей на множества, то у первого множества( дверь, которую выбрали вы) 1/50, а у второго множества (все остальные двери) 49/50.

Согласитесь, что вероятность вашего попадания с первого раза, в случае с пятьюдесятью дверями, довольно мала, поэтому, когда вам предлагают изменить свой выбор, любой рационально мыслящий человек должен принять предложение.
Да, многие могут сказать, что в случае с тремя дверями вероятность с первого раза указать на правильную дверь намного больше, но по сути, процентное соотношения второй группы все равно останется преобладающим.

Эксперимент на доказательство парадокса Монти Холла :
Чтобы доказать или опровергнуть данный парадокс достаточно провести несложный эксперимент. Эксперимент - лучшее средство проверки достоверности. В моем опыте мне помогали две мои подруги и одноклассницы - Пуйшо Арина и Солдатенкова Вика.

Из оборудования у нас было :
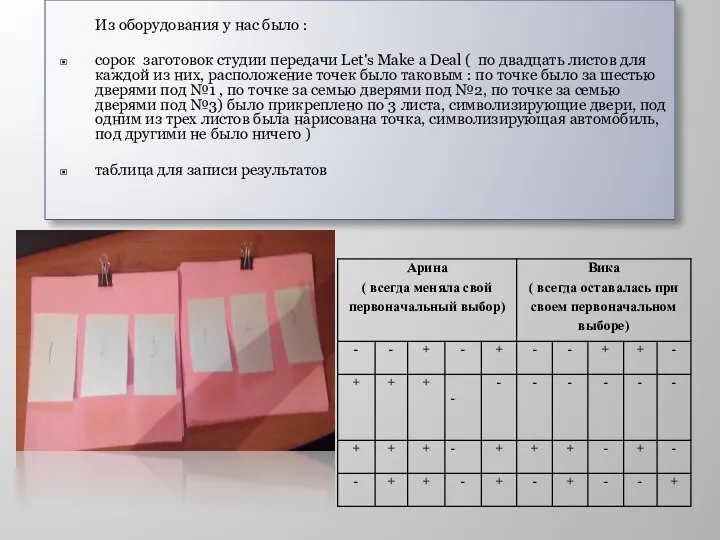
сорок заготовок студии передачи Let's Make a Deal ( по двадцать листов для каждой из них, расположение точек было таковым : по точке было за шестью дверями под №1 , по точке за семью дверями под №2, по точке за семью дверями под №3) было прикреплено по 3 листа, символизирующие двери, под одним из трех листов была нарисована точка, символизирующая автомобиль, под другими не было ничего )
таблица для записи результатов

Итог эксперимента
У меня не было возможность проделать этот эксперимент с большим количеством людей, поэтому я попросила Арину всегда менять свой выбор, после того, как я открываю одну из дверей, а Вику я попросила всегда оставаться при своем первоначальном мнении.
Я была в роли ведущего и заранее знала за кокой из бумажек (дверей) окажется автомобиль (точка), для Арины и Вики это было секретом.
На проведение самого эксперимента нам понадобилась 20 минут, 30 минут у нас ушло на подготовку, 5 минут на подсчет результатов.
Итоги нашего эксперимента (приложение №1 ) показали, что стратегия смены выбора является наиболее выигрышной . Арина выиграла 13 раз из 20 возможных, а Вика выиграла всего лишь 6 раз. Стратегия смены решения почти в два раза результативнее.