Показательная функция

ЦЕЛЬ УРОКА
обучающий аспект:
ввести понятие показательной функции;
учить строить график показательной функции;
рассмотреть свойства показательной функции;
развивающий аспект:
развивать грамотную математическую речь при ответе с места и у доски;
развивать мышление посредством:
анализа и синтеза при работе над выводом алгоритма
постановки и решения проблемы (логические умозаключения при возникновении проблемной ситуации и ее разрешении);
воспитывающий аспект:
воспитывать соблюдение норм поведения в коллективе, уважение к мнению окружающих при совместной деятельности в группах.

РЕАЛЬНЫЕ ПРОЦЕССЫ

ЗАДАНИЕ №1

Зная, что = 1,7320508...
Если мы рассмотрим последовательность рациональных чисел – десятичных приближений числа по недостатку или по избытку, мы докажем, что эта последовательность сходится, значит функция непрерывна на множестве действительных чисел.
Поэтому мы можем соединить эти точки и получим график показательной функции.

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ
Функция, заданная формулой y = ax
(a > 0, а ≠ 1, х R), называется показательной функцией.

ЛЕГЕНДА О ШАХМАТАХ
Впервые легенда о награде за изобретении шахмат встречается в ХI веке н.э. в книге арабского учёного Аль Бируни.
Она гласит о том, что
за первую клетку шахматной доски изобретатель потребовал от царя 1 пшеничное зернышко,
за вторую клетку – 2,
за третью – 4,
за четвертую – 8 и т.д.
И для того чтобы найти сколько же потребовал изобретатель, нужно сложить члены геометрической прогрессии: 1, 2, 4, 8, …, 263. Эта сумма равна 264 – 1, т.е. 184467440737095551615.

ИСТОРИЯ ВОЗНИКНОВЕНИЯ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ
В дальнейшем появляются в Западной Европе (это ХIV – XV в.) банки, которые давали деньги под большие проценты. И при этом приходилось делать большие, сложные расчеты.
Вскоре появляется идея степени с дробным показателем, потом создаются таблицы логарифмов и антилогарифмов.
Оставался один шаг, чтобы ввести степени с любым действительным показателем. И этот шаг, в конце концов, был сделан в конце XVII в. Исааком Ньютоном.
И уже после этого Иоганн Бернулли рассмотрел степени с переменным действительным показателем, т.е. ввёл показательную функцию.

Среди заданных функций укажите те, которые являются показательными:
а) y = 3х
б) y = х3
в) y =
г) y =
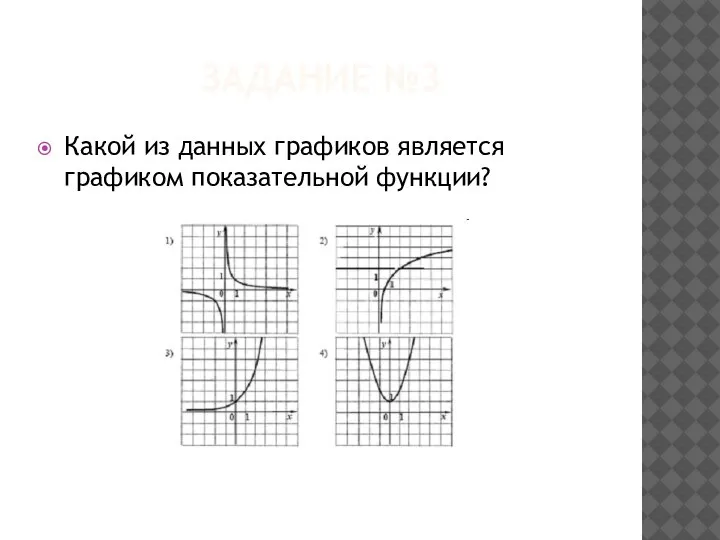
ЗАДАНИЕ №2

ЗАДАНИЕ №3
Какой из данных графиков является графиком показательной функции?

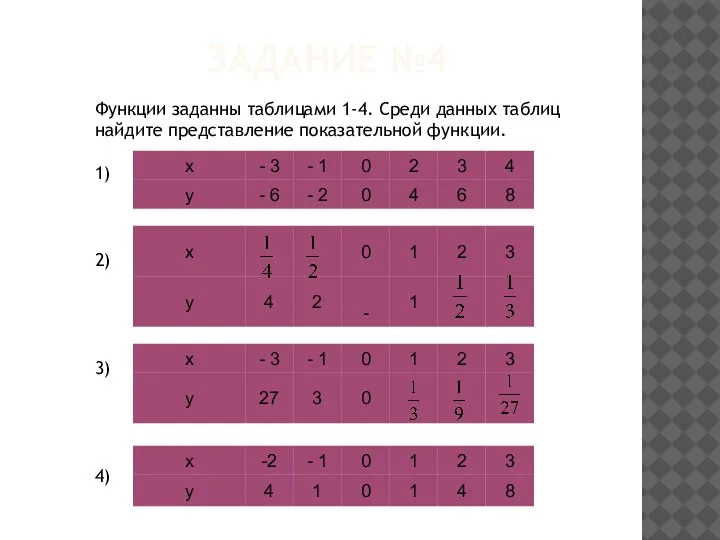
Функции заданны таблицами 1-4. Среди данных таблиц найдите представление показательной функции.
1)
2)
3)
4)
ЗАДАНИЕ №4

ЗАДАНИЕ №5
Заполните пропуски.
Функцию вида y = ax , где ____ и _____, называется показательной функцией.

ЗАДАНИЕ №5
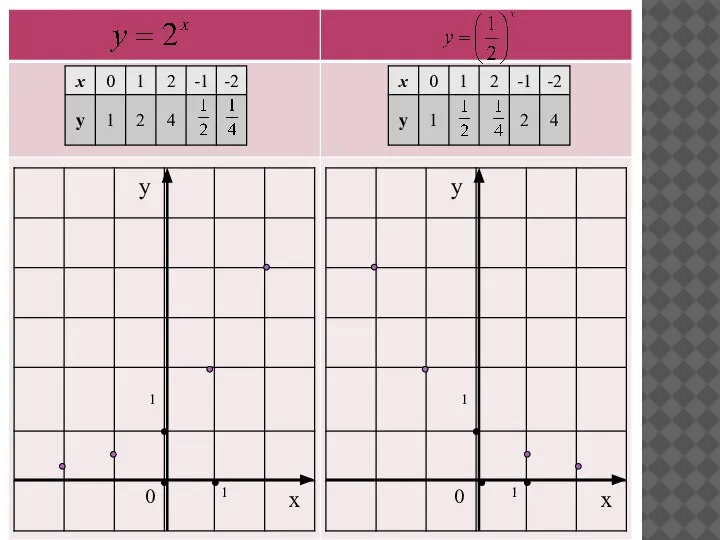
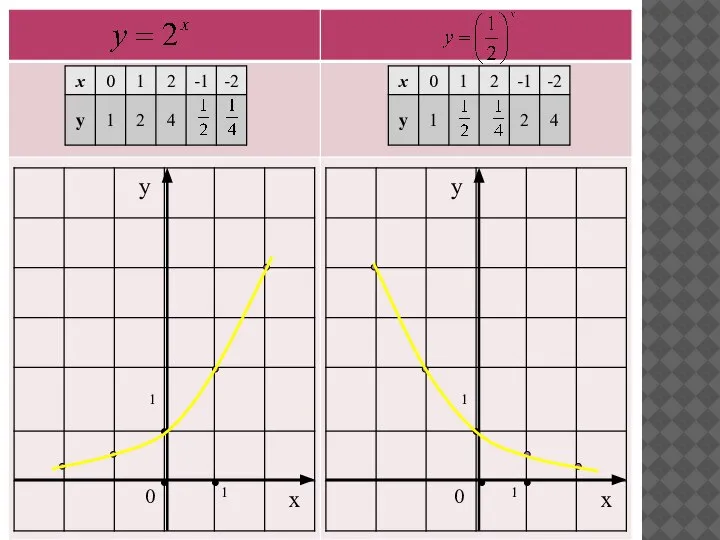
Найдите значение показательной функции при заданных значениях х: