Показательная функция. Показательные уравнения и неравенства. Урок закрепления знаний

а) Все заданные функции являются показательными:

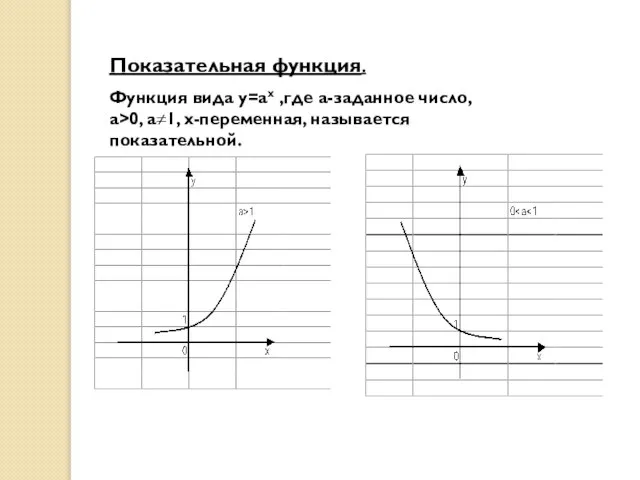
Показательная функция.
Функция вида у=ах ,где а-заданное число, а>0, а≠1, х-переменная, называется показательной.

Показательная функция обладает следующими свойствами:
Д(у): множество R всех действительных чисел;
Е(у):множество всех положительных чисел;
Показательная функция у=ах является возрастающей на множестве всех действительных чисел, если а>1,и убывающей, если 0<а<1;
Свойства степеней:
=

Показательные уравнения.
Уравнения, у которых неизвестное находится в показателе степени, называются показательными.
При решении показательных уравнений:
Обе части уравнения приводятся к степени с одинаковым основанием.
Приравниваются показатели степеней.
Способы решения:
По свойству степени;
Вынесение общего множителя за скобки;
Деление обеих частей уравнения на одно и то же выражение, принимающее значение отличное от нуля при всех действительных значениях х;
Способ группировки;
Сведение уравнения к квадратному;
Графический.

Решите задания В5 ЕГЭ :

Используя свойства возрастания и убывания показательной функции, можно сравнить числа и решать показательные неравенства
Неравенства, у которых неизвестное находится в показателе степени, называются показательными.
Решение показательных неравенств сводится к решению неравенств ах>ав или ах<ав.
Если а>1, то х>в (х<в).
Если 0<а<1. то х<в (х>в).
При решении показательного неравенств
Обе части неравенства приводятся к степени с одинаковым основанием.
Сравниваются показатели с применением свойства возрастания и убывания показательной функции:
- если основание больше 1, то знак неравенства для показателей сохраняется,
- если основание меньше 1, то знак неравенства для показателей меняется на противоположный.

Способы решения показательных неравенств.
1. По свойству степени;
2. Вынесение общего множителя за скобки;
3.Сведение к квадратному;
4. Графический.
Сравните:
а) 53 и 55; б) 47 и 43; в) 0,22 и 0,26;
г) 0,92 и 0,9.
Решите:
а) 2х>1; б) 13х+1<133; в) 0,7х-2>0,7;
г) 0,04х<0,22.

Спасибо за урок!