Содержание
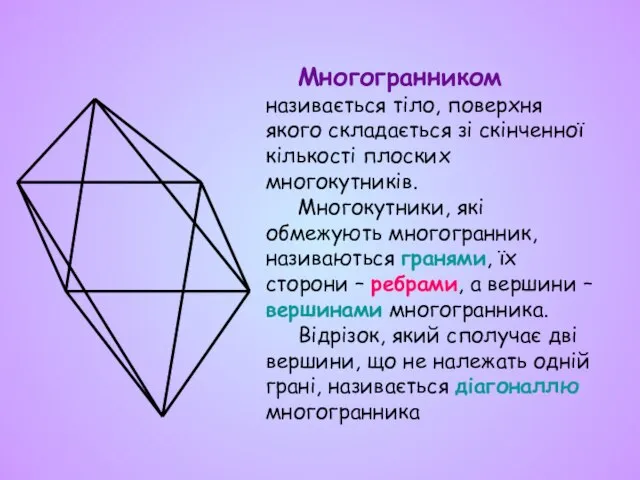
- 2. Многогранником називається тіло, поверхня якого складається зі скінченної кількості плоских многокутників. Многокутники, які обмежують многогранник, називаються
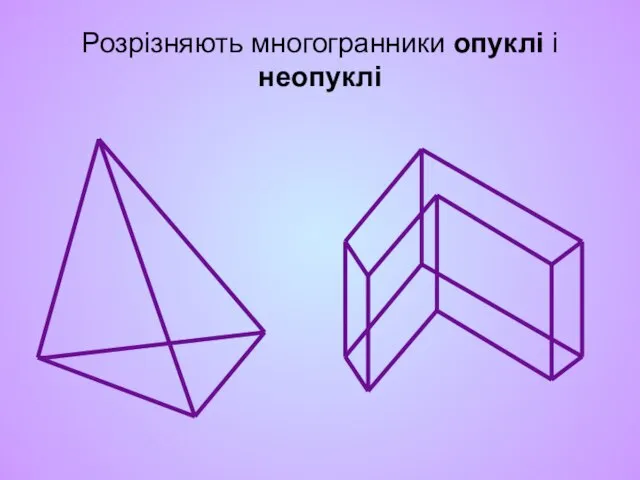
- 3. Розрізняють многогранники опуклі і неопуклі
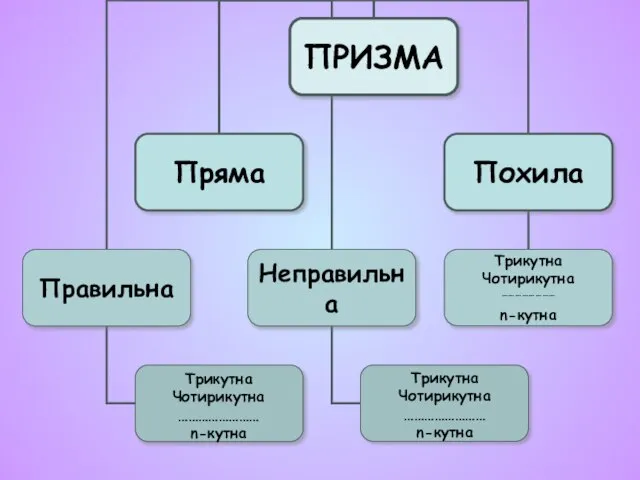
- 5. ПРИЗМА Призмою називається многогранник, який складається з двох плоских многокутників, які лежать у різних площинах і
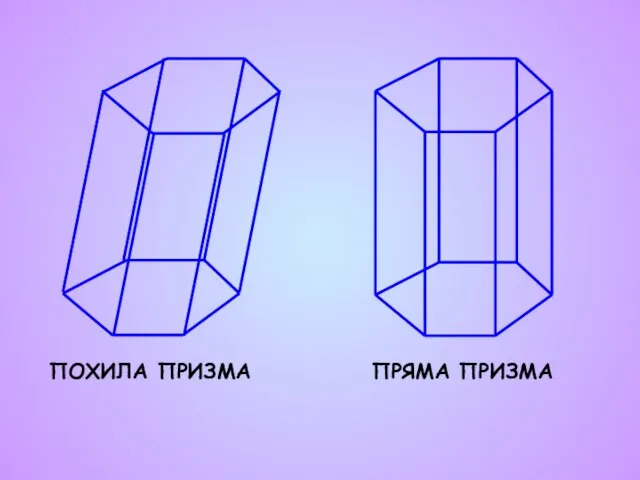
- 6. ПРЯМА ПРИЗМА ПОХИЛА ПРИЗМА
- 7. Трикутна Чотирикутна …………………… n-кутна Трикутна Чотирикутна …………………… n-кутна
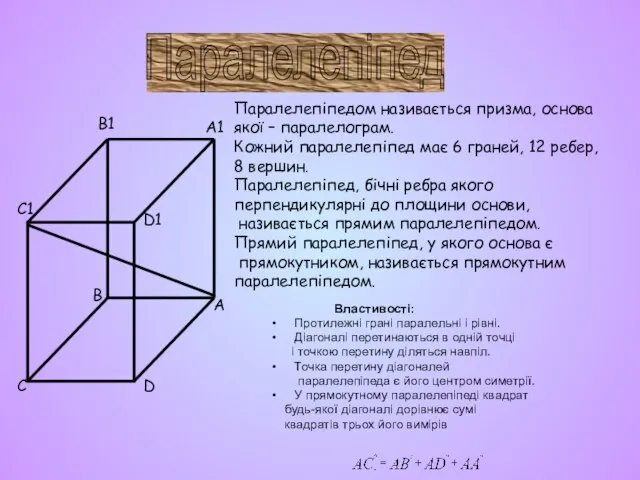
- 8. Властивості: Протилежні грані паралельні і рівні. Діагоналі перетинаються в одній точці і точкою перетину діляться навпіл.
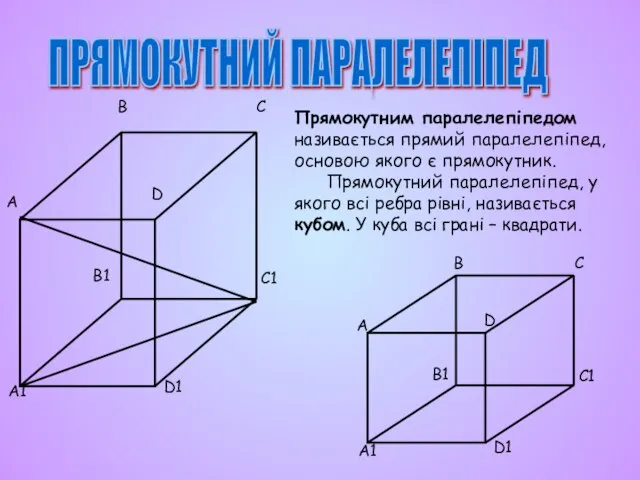
- 9. ПРЯМОКУТНИЙ ПАРАЛЕЛЕПІПЕД Прямокутним паралелепіпедом називається прямий паралелепіпед, основою якого є прямокутник. Прямокутний паралелепіпед, у якого всі
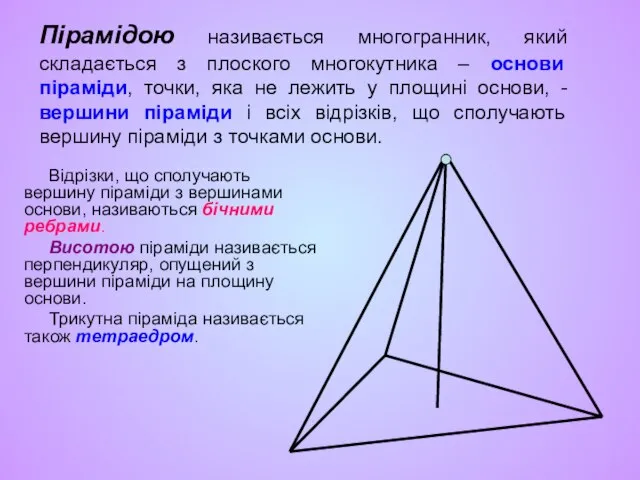
- 10. Пірамідою називається многогранник, який складається з плоского многокутника – основи піраміди, точки, яка не лежить у
- 11. Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього
- 12. Многогранник називається правильним, якщо всі його грані – рівні правильні многокутники, а всі вершини рівновіддалені від
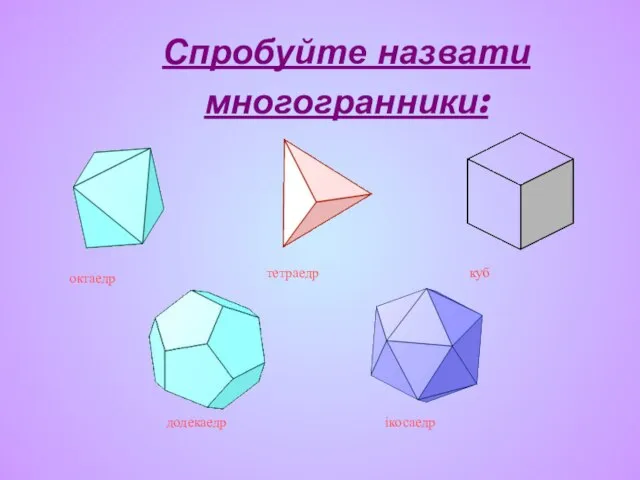
- 13. Спробуйте назвати многогранники: тетраедр куб октаедр додекаедр ікосаедр
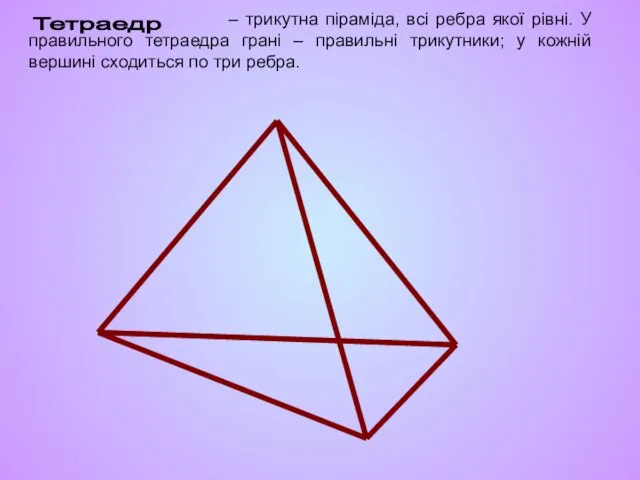
- 14. – трикутна піраміда, всі ребра якої рівні. У правильного тетраедра грані – правильні трикутники; у кожній
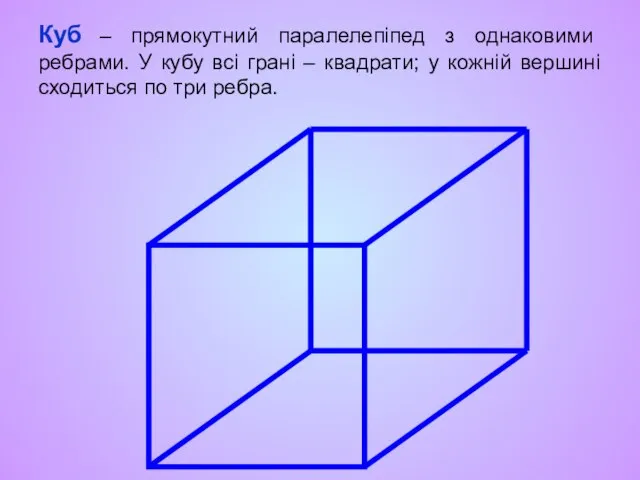
- 15. Куб – прямокутний паралелепіпед з однаковими ребрами. У кубу всі грані – квадрати; у кожній вершині
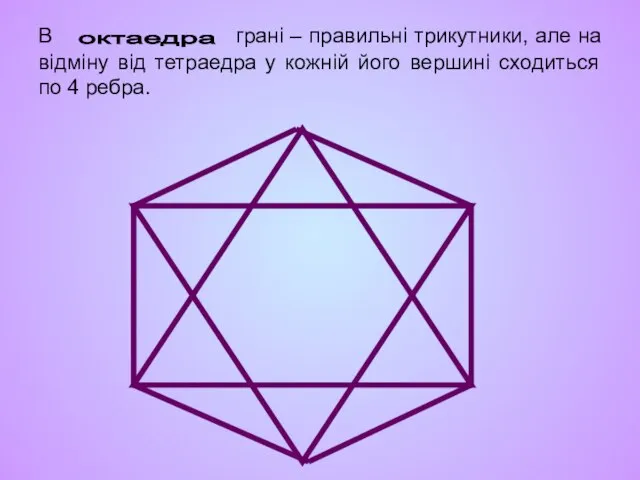
- 16. В грані – правильні трикутники, але на відміну від тетраедра у кожній його вершині сходиться по
- 17. У грані – правильні п’ятикутники. У кожній вершині його сходиться по три ребра. додекаедра
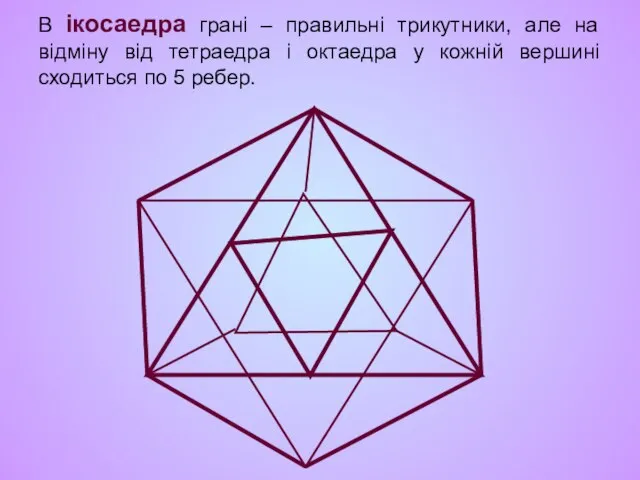
- 18. В ікосаедра грані – правильні трикутники, але на відміну від тетраедра і октаедра у кожній вершині
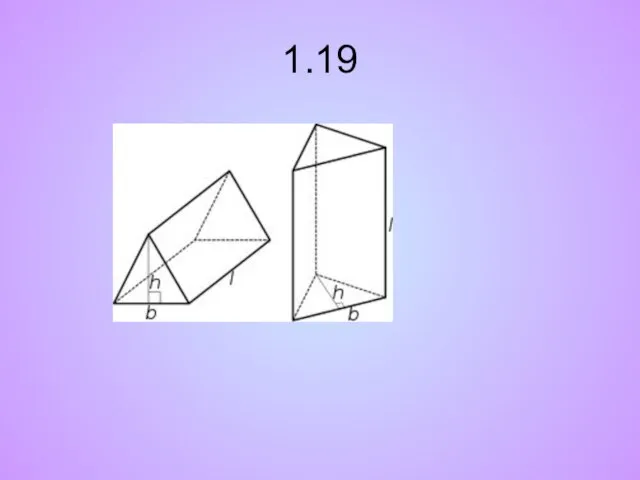
- 20. 1.19
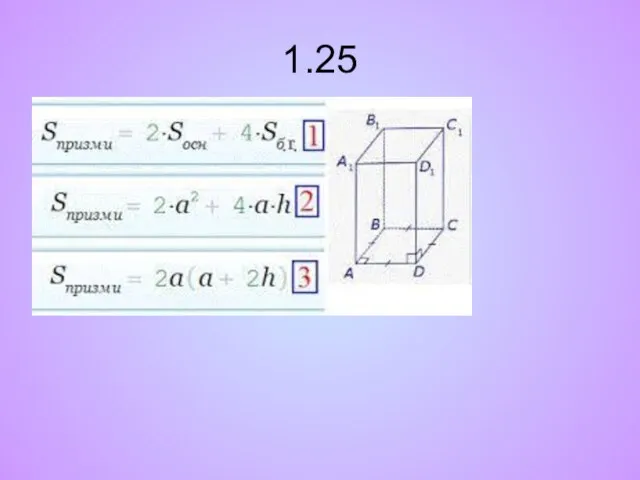
- 21. 1.25
- 23. Скачать презентацию




 Алгебраические определения
Алгебраические определения Старинные задачи на дроби
Старинные задачи на дроби Графики уравнений
Графики уравнений Подготовка к СОЧ
Подготовка к СОЧ Логарифмы. Свойства логарифмов
Логарифмы. Свойства логарифмов Координатная плоскость
Координатная плоскость Численные методы. Вычислительная математика
Численные методы. Вычислительная математика Презентация на тему Многогранники
Презентация на тему Многогранники  Развёртка куба
Развёртка куба idkwhythatair
idkwhythatair Векторное кодирование графической информации
Векторное кодирование графической информации Вычисление предела
Вычисление предела Элементы математической статистики
Элементы математической статистики Презентация на тему Логарифмы с параметрами
Презентация на тему Логарифмы с параметрами  Презентация на тему Задачи на увеличение и уменьшение числа (1 класс)
Презентация на тему Задачи на увеличение и уменьшение числа (1 класс)  Решение линейных неравенств
Решение линейных неравенств Задача №12. 9 класс
Задача №12. 9 класс История появления дробей
История появления дробей  Основные понятия комбинаторики. Факториал. Вычисление факториала
Основные понятия комбинаторики. Факториал. Вычисление факториала Презентация на тему КВАДРАТИЧНАЯ ФУНКЦИЯ И КВАДРАТИЧНЫЕ НЕРАВЕНСТВА
Презентация на тему КВАДРАТИЧНАЯ ФУНКЦИЯ И КВАДРАТИЧНЫЕ НЕРАВЕНСТВА  Краткая запись задач
Краткая запись задач Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика 797329 (1)
797329 (1) Неполные квадратные уравнения
Неполные квадратные уравнения Задачи, решаемые геометрическим моделированием
Задачи, решаемые геометрическим моделированием Подготовка к контрольной работе. Уравнения
Подготовка к контрольной работе. Уравнения Задачи на готовом чертеже. 9 класс
Задачи на готовом чертеже. 9 класс Пифагор и его египетский треугольник
Пифагор и его египетский треугольник