Содержание
- 2. Сочетания и размещения. При подсчете вероятности события, иногда бывает довольно таки сложно подсчитать общее количество исходов.
- 3. Сочетания и размещения. Количество перестановок из n элементов, можно вычислять используя следующую теорему: Теорема. N отличных
- 4. Сочетания и размещения. Пример. К Иван Васильевичу пришли гости: Александр, Алексей, Петр и Николай. За столом
- 5. Сочетания и размещения. Пример. В чемпионате по хоккею участвовало восемь команд, каждая команда сыграла с другой
- 6. Сочетания и размещения. Второй способ: Пронумеровав или зная названия команд можно подсчитать, что первая команда сыграет
- 7. Сочетания и размещения. Количество сочетаний из n элементов по 2 легко вычисляется по формуле: Теорема. Для
- 8. Сочетания и размещения. Пример. Ребята 11 А и 11 Б решили поиграть в шахматы. В 11
- 9. Сочетания и размещения. Часто встречаются задачи, в которых порядок размещения элементов важен, тогда нам следует воспользоваться
- 10. Сочетания и размещения. Пример. В классе 20 учеников. К доске нужно вызвать двух человек, сколькими способами
- 11. Сочетания и размещения. Мы рассмотрели случай когда в выборе участвовало 2 элемента, а как же быть
- 12. Сочетания и размещения. Пример. В классе 25 учеников, нужно выбрать 4 ученика таким образом: а) Один
- 13. Сочетания и размещения. В конце урока запишем ряд важных свойств: 1) 0!=1 2) 3) 4) Давайте
- 15. Скачать презентацию












 Алгоритмы на графах
Алгоритмы на графах Устная нумерация чисел от 1 до 20
Устная нумерация чисел от 1 до 20 Числовi послiдовностi. Властивостi числових послiдовностей
Числовi послiдовностi. Властивостi числових послiдовностей Решение тригонометрических уравнений
Решение тригонометрических уравнений Окружность
Окружность Предел последовательности
Предел последовательности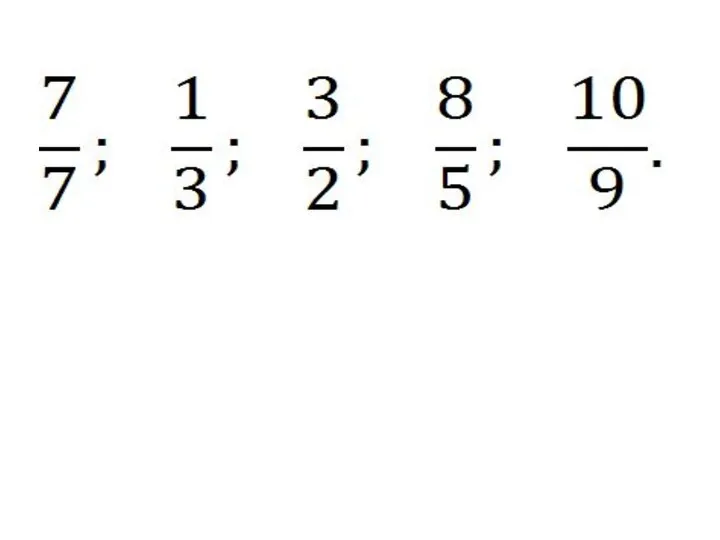 Знак деления
Знак деления Деление одночлена на одночлен
Деление одночлена на одночлен Решаем задачи
Решаем задачи Системы принятия решений
Системы принятия решений Возвратные уравнения
Возвратные уравнения Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики?
Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики? Куб. Теорема Эйлера
Куб. Теорема Эйлера Решение иррациональных уравнений. Разные методы
Решение иррациональных уравнений. Разные методы Решение тригонометрических неравенств
Решение тригонометрических неравенств Тригонометрические уравнения и математические термины на английском языке
Тригонометрические уравнения и математические термины на английском языке Сложение и вычитание многочленов
Сложение и вычитание многочленов Производная функции. Тест 1
Производная функции. Тест 1 Основы дисперсионного анализа
Основы дисперсионного анализа Неопределённый интеграл. Элементы интегрального исчисления
Неопределённый интеграл. Элементы интегрального исчисления Сравнение предметов. Счет до 5
Сравнение предметов. Счет до 5 Формулы половинного аргумента
Формулы половинного аргумента Пирамида и её элементы. Правильная пирамида
Пирамида и её элементы. Правильная пирамида Шар. Куб. Параллелепипед
Шар. Куб. Параллелепипед Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна
Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна Таблицы истинности
Таблицы истинности Плоскость касательной к сфере
Плоскость касательной к сфере Задачи на готовых чертежах. Ромб
Задачи на готовых чертежах. Ромб