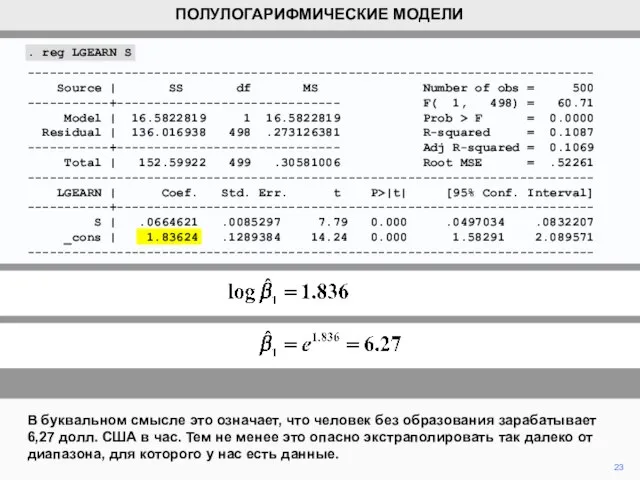
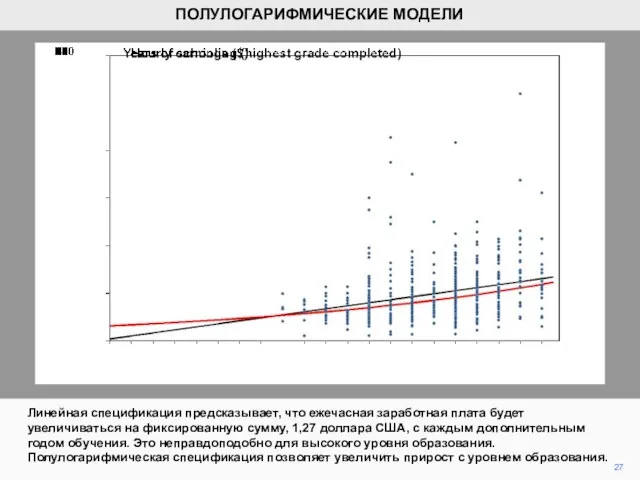
США в час. Тем не менее это опасно экстраполировать так далеко от диапазона, для которого у нас есть данные.
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
. reg LGEARN S
Source | SS df MS Number of obs = 540
-------------+------------------------------ F( 1, 538) = 140.05
Model | 38.5643833 1 38.5643833 Prob > F = 0.0000
Residual | 148.14326 538 .275359219 R-squared = 0.2065
-------------+------------------------------ Adj R-squared = 0.2051
Total | 186.707643 539 .34639637 Root MSE = .52475
------------------------------------------------------------------------------
LGEARN | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
S | .1096934 .0092691 11.83 0.000 .0914853 .1279014
_cons | 1.292241 .1287252 10.04 0.000 1.039376 1.545107
------------------------------------------------------------------------------
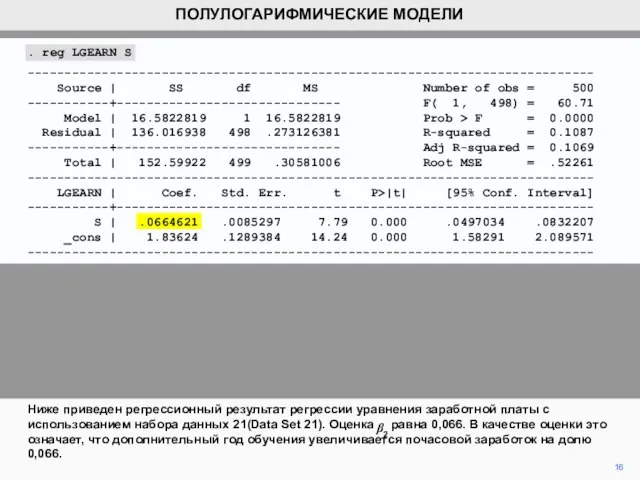
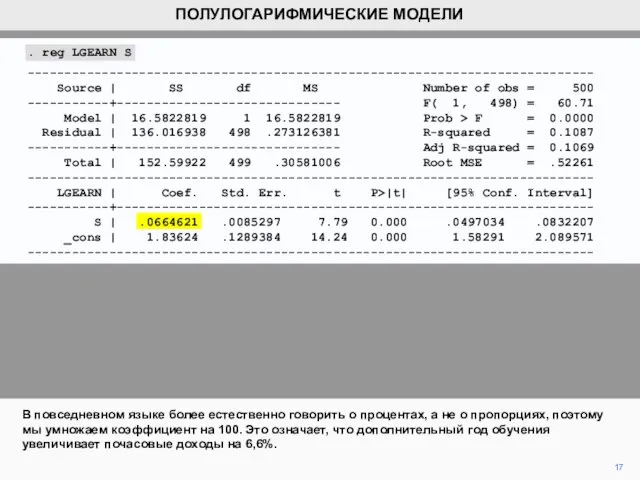
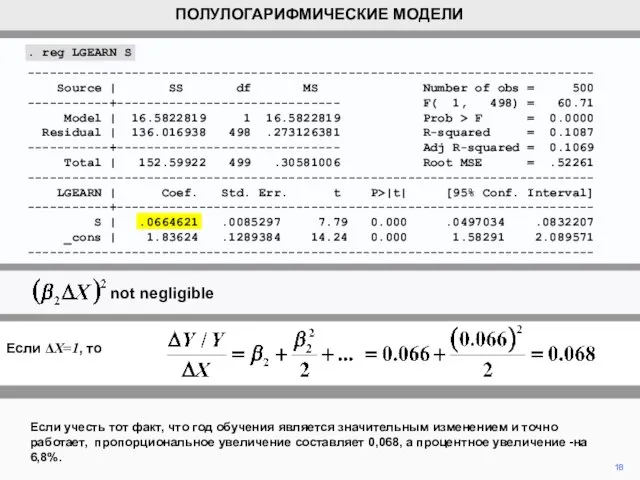
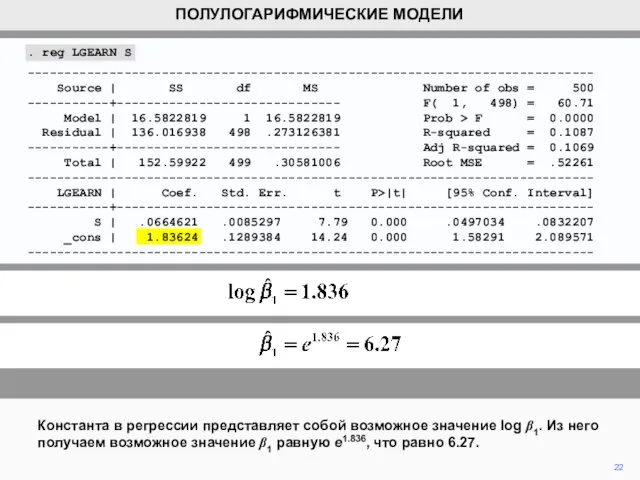
. reg LGEARN S
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 1, 498) = 60.71
Model | 16.5822819 1 16.5822819 Prob > F = 0.0000
Residual | 136.016938 498 .273126381 R-squared = 0.1087
-----------+------------------------------ Adj R-squared = 0.1069
Total | 152.59922 499 .30581006 Root MSE = .52261
----------------------------------------------------------------------------
LGEARN | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
S | .0664621 .0085297 7.79 0.000 .0497034 .0832207
_cons | 1.83624 .1289384 14.24 0.000 1.58291 2.089571
----------------------------------------------------------------------------

















 Сложение и вычитание смешанных чисел. Графический диктант
Сложение и вычитание смешанных чисел. Графический диктант Раз, два, три. Спортивно-математический турнир
Раз, два, три. Спортивно-математический турнир Точка, прямая, отрезок. Математический диктант
Точка, прямая, отрезок. Математический диктант Как умножали египтяне
Как умножали египтяне Корень уравнения
Корень уравнения Матрицы
Матрицы Решение треугольников
Решение треугольников Презентация на тему Число и цифра 4
Презентация на тему Число и цифра 4  Отделение математических наук РАН
Отделение математических наук РАН Векторное кодирование графической информации
Векторное кодирование графической информации Классическое определение вероятности
Классическое определение вероятности Квадратный корень из степени
Квадратный корень из степени Математический анализ. Лекция 2
Математический анализ. Лекция 2 Метод координат в пространстве
Метод координат в пространстве Признаки подобия треугольников
Признаки подобия треугольников Тригонометрия. Подготовка к диагностической работе
Тригонометрия. Подготовка к диагностической работе Мысли о ЕГЭ
Мысли о ЕГЭ Алгебраические структуры, порожденные отношением причинности на пространствах-временах
Алгебраические структуры, порожденные отношением причинности на пространствах-временах Временные ряды
Временные ряды Треугольники и их виды
Треугольники и их виды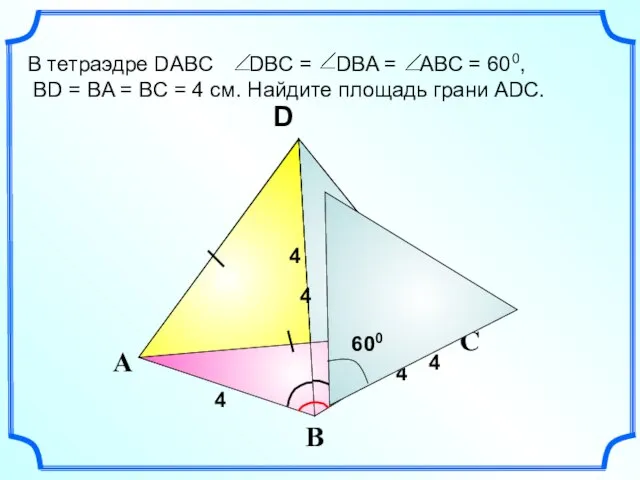 Тетраэдр. Свойства тетраэдра
Тетраэдр. Свойства тетраэдра Окружность и прямая
Окружность и прямая Площадь многоугольника
Площадь многоугольника Презентация по математике "Число 7" -
Презентация по математике "Число 7" -  Презентация на тему Средняя линия треугольника
Презентация на тему Средняя линия треугольника  Сложение и умножение вероятностей. Полная вероятность. Формула Бейеса. Лекция 2
Сложение и умножение вероятностей. Полная вероятность. Формула Бейеса. Лекция 2 Аналитическая геометрия. Прямая на плоскости
Аналитическая геометрия. Прямая на плоскости Tema1_TeoriaMnozhestv
Tema1_TeoriaMnozhestv