Содержание
- 2. Средняя величина это обобщающий показатель, который характеризует типичный уровень явления в конкретных условиях места и времени.
- 3. Виды средней величины Выбор вида средней определяется содержанием показателя и исходных данных. В каждом конкретном случае
- 4. Средняя арифметическая простая где х1 , х2, х3 , … xn— индивидуальные значения варьирующего признака (варианты);
- 5. Средняя арифметическая взвешенная применяется в тех случаях, когда данные представлены в виде рядов распределения или группировок.
- 6. Средняя геометрическая простая i
- 7. Средняя геометрическая взвешенная
- 8. Средняя гармоническая простая i
- 9. Средняя гармоническая взвешенная Где zi (wi) - веса
- 10. Средняя квадратическая простая где хi - варианты; n - число единиц совокупности
- 11. Средняя квадратическая взвешенная где хi — варианта; fi — повторяемость индивидуальных значений признака (частота).
- 12. Средние величины Важнейшими условиями (принципами) для правильного вычисления и использования средних величин является следующие: В каждом
- 13. Средние величины При расчете различных средних по одним и тем же данным значения средних будут неодинаковыми,
- 15. Средняя структурная. Мода Модой (Мо) называется наиболее часто встречающееся или типичное значение признака, или модой называется
- 16. Мода (для интервального ряда) где: xMo – нижняя граница модального интервала; iMo – величина модального интервала;
- 17. Средняя структурная. Медиана Медиана (Ме) – это величина, которая делит численность упорядоченного вариационного ряда на две
- 18. Средняя структурная. Медиана (для интервального ряда) где: x Me – нижняя граница медианного интервала; iMe –
- 19. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Средние величины
- 20. Пример 3 Имеется информация о стаже работников банка (см. табл.) Определите: Средний стаж работников банка. Модальный
- 21. Пример 3 Алгоритм решения: Закрыть интервалы (первый и последний интервалы ряда - открытые). Найти срединные значения
- 22. ПОКАЗАТЕЛИ ВАРИАЦИИ Статистические показатели
- 23. Показатели вариации Используются для установления типичности или показательности средней величины, т.е. насколько точно характеризует средняя данную
- 24. Показатели вариации Размах вариации (R). Среднее линейное отклонение ( ). Дисперсия (σ2). Среднее квадратичное отклонение (σ).
- 25. Размах вариации Это разность между максимальным и минимальным значениями признака:
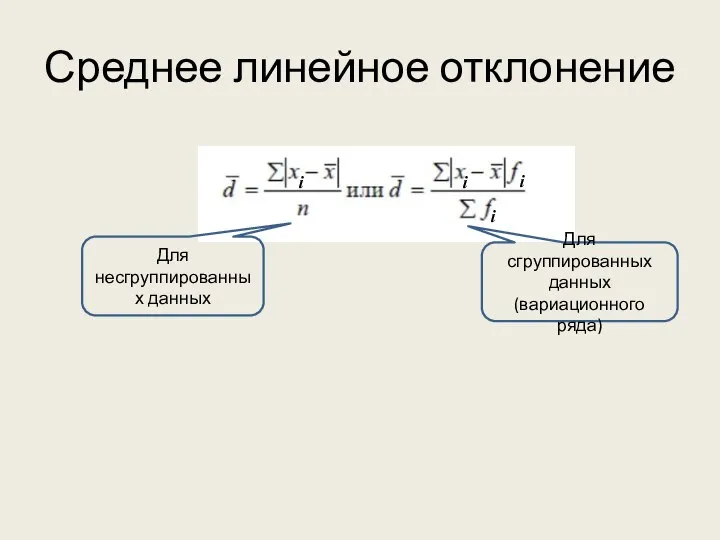
- 26. Среднее линейное отклонение Для несгруппированных данных Для сгруппированных данных (вариационного ряда)
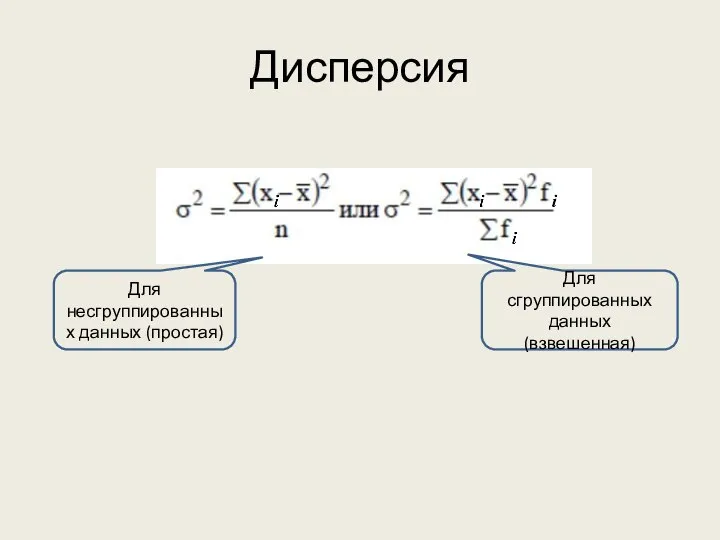
- 27. Дисперсия Для несгруппированных данных (простая) Для сгруппированных данных (взвешенная)
- 28. Среднее квадратическое отклонение Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем
- 29. Коэффициент вариации Это выраженное в % отношение среднего квадратического отклонения к средней арифметической: Статистическая совокупность считается
- 30. Пример 2. Решение задач (был рассмотрен ранее) При проведении плановых мероприятий по выявлению нарушений скоростного режима
- 31. Пример 4 На основании приведенных в примере 2 данных и построенного вариационного ряда определите: Среднюю скорость
- 33. Скачать презентацию




























 Алгоритмы направленного перебора
Алгоритмы направленного перебора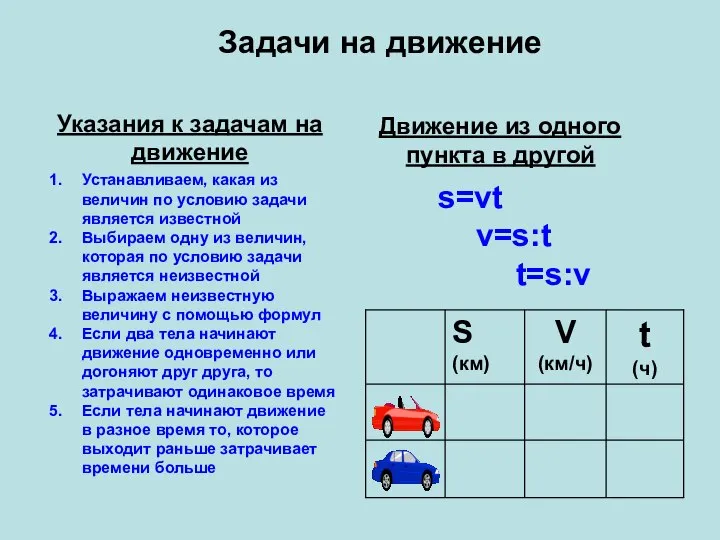 Задачи на движение Указания к задачам на движение
Задачи на движение Указания к задачам на движение Графики функций
Графики функций Квадратичная функция
Квадратичная функция Арифметическая прогрессия
Арифметическая прогрессия Космос
Космос Поворот и центральная симметрия
Поворот и центральная симметрия Теорема Виета
Теорема Виета Иллюстрации географических объектов на Луне
Иллюстрации географических объектов на Луне Математика в карточных фокусах
Математика в карточных фокусах Примеры
Примеры Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля
Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля  Понятие вектора
Понятие вектора Бином Ньютона. Треугольник Паскаля
Бином Ньютона. Треугольник Паскаля Решение задач на прямую и обратную пропорциональность
Решение задач на прямую и обратную пропорциональность Распознавание и называние геометрических фигур
Распознавание и называние геометрических фигур Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Функция. График функции
Функция. График функции Сайы. Умумий малюмат
Сайы. Умумий малюмат Презентация на тему Обыкновенные дроби (6 класс)
Презентация на тему Обыкновенные дроби (6 класс)  Контрольная работа № 9
Контрольная работа № 9 Геометрия на каждом уроке
Геометрия на каждом уроке Наименьшее и наибольшее значение функции. Задачи
Наименьшее и наибольшее значение функции. Задачи Способы решения задач на смеси и сплавы
Способы решения задач на смеси и сплавы Площадь фигур. Решение задач
Площадь фигур. Решение задач Подготовка к ВПР
Подготовка к ВПР Решение квадратных уравнений. Повторительно-обобщающий урок
Решение квадратных уравнений. Повторительно-обобщающий урок Математика для детей (игры)
Математика для детей (игры)